原假设和备择假设可以互换位置吗？这是一个经常被问到的问题，事实上我们⼀般只会把想要推翻的结论放在原假设上，而很少会反过来。

假设检验中有两个互补的假设：原假设（null hypothesis）和备择假设 （alternative hypothesis），分别⽤ H0 和 H1 来表⽰。

假设检验的过程就是使⽤一些抽样所得的数据作为「证据」试图推翻原假设的过程，这个过程与法官判案的过程类似。抽样所得的数据事实上不一定是事实之全部，所以我们才需要有假设检验。

在法律上有所谓的「⽆罪推定原则（presumption of innocence）」，即对于犯罪嫌疑⼈，必须先假设其⽆罪，原告⽅有义务提出证据证明其犯罪，⽽不得强迫嫌疑⼈⾃证其罪。

使⽤以上术语，即原假设（H0）为 被告⽆罪，备择假设（H1）为被告有罪，假设检验的⽬的就是使⽤证据（样本数据）试图推翻原假设（⽆罪）。如果现有证据可以推翻原假设，那么我们称为拒绝原假设（rejecting H0），即可以认为原假设为假；⽽如果现有证据不能推翻原假设，即没有充⾜的证据证明原假设为假，那么我们称不能拒绝原假设（not rejecting H0）。

注意「接受原假设（accepting H0）」的说法与「不能拒绝原假设」的说法有细微差别，如果不能拒绝原假设，可能是由于我们的证据不够充分，因⽽「不能拒绝原假设」的说法更加准确。基于上述原因，我们⼀般会把想要推翻的结论放在原假设上。

由于统计⽅法总会存在误差，因⽽基于以上两类假设的推断也会存在犯错的可能性。在假设检验中，有两种错误可能会发⽣：

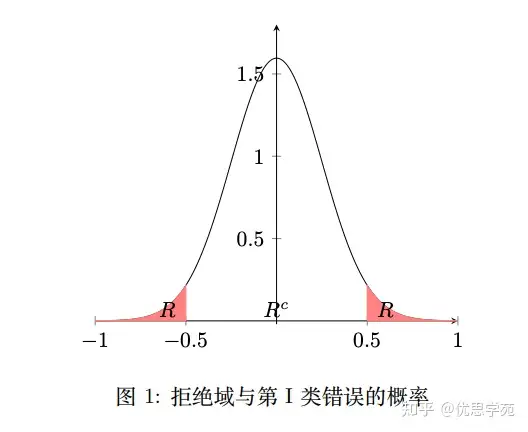
1. 第 I 类错误：原假设为真，但是拒绝原假设，即「弃真错误」；

2. 第 II 类错误：备择假设为真，但是接受原假设，即「取伪错误」。

⽐如，如果⼀个被告本来⽆罪，但是错误地判其有罪，那么就犯了第 I 类错误； ⽽如果⼀个被告的确犯罪，但是却判其⽆罪，那么就犯了第 II 类错误。

在质量管理中，我们经常需要回答这样的问题，例如：改进后的生产流程是否真的降低了不合格率？新供应商的产品质量是否与原供应商一致？新检测设备是否比旧设备更精准？这些时候假设检验就非常有用。