五年级闺女哭着说这道题自己算了20分钟了，就是算不出答案，题目是不是缺少条件？ 如图所示，两个正方形并排摆放，小正方形的边长是10厘米，求阴影部分面积？ 阴影部分是两个三角形，如果尝试求每一个三角形面积并不好思考，所以可以考虑利用辅助线借助等积转换解答题目，这道题还是有些难度。#五年级几何题#
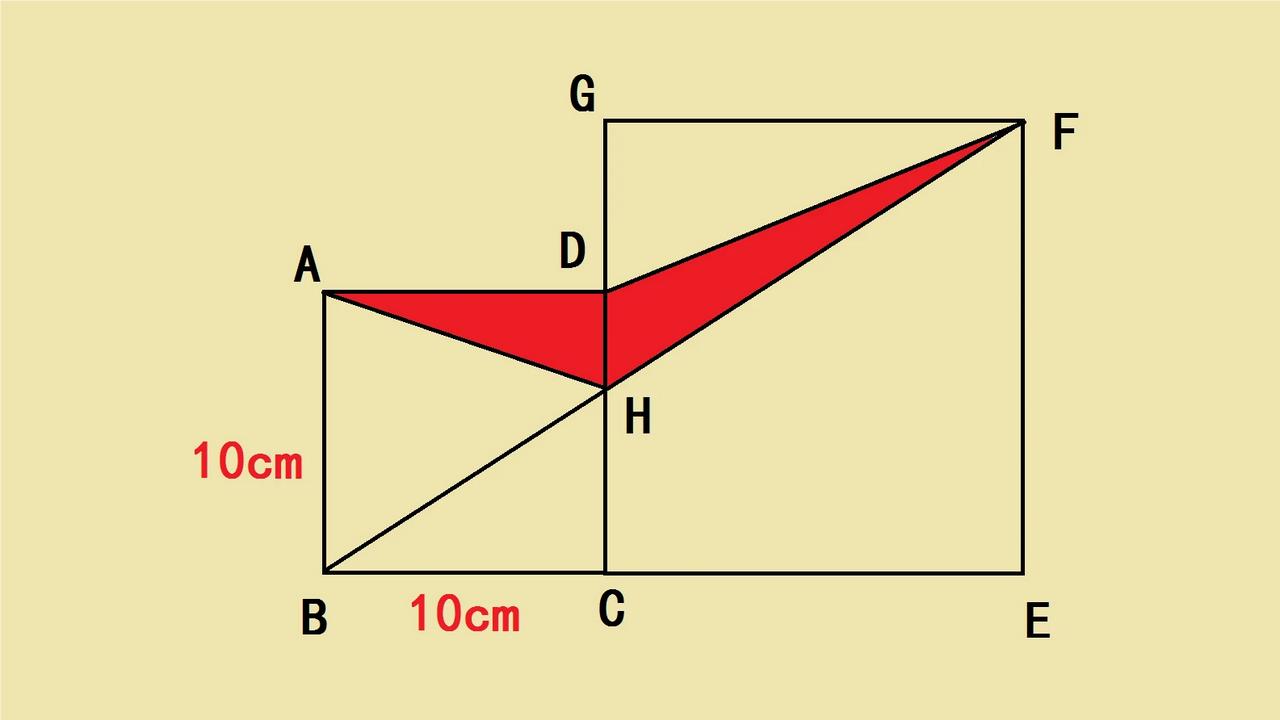
五年级闺女哭着说这道题自己算了20分钟了，就是算不出答案，题目是不是缺少条件？
大力小学数学吖
2024-09-29 12:20:06
0
阅读：4222
油腻大叔
设大正方形边长为a，阴影部分面积=小正方形面积+大正方形面积-GDF-BEF-ABH。所以S阴=10²+a²-（a-10）a/2-（a+10）a/2-10²/2，计算中可以发现a可以完全去掉，最终答案为50。
东方红日 回复 10-02 06:58
你太牛了！👍👍👍
喂，是你 回复 09-30 17:51
当大正方形CGFE无限大时，△DHF的面积也是一成不变的吗？
傻得有水平
连BD，CF。同底等高易知S△ADH=S△BDH 因BD∥CF，故以BD为底来看C、F均在BD平行线CF上 S△BDF=S△BDC=110×10/2=50
闲着没事随意说 回复 12-15 21:50
[点赞]
石头
判断有没有解从几个奇异点开始，大正方形可变，如果D.H同点即面积为0
帅老师 回复 12-21 09:44
DH不可能重合
用户55xxx54 回复 10-04 18:41
审题没有，题目都写了如图所示，大正方形还变啥变
追风的中年人
直接拉窗帘，连接BD，CF，则有△ADH=△BDH，△BDF=△BCD=50
喂，是你
假设大正方形边长为20cm，△BCH≌△FGH，BC/FG=CH/GH,10/20=CH/(20-CH),DH=10/3cm, S△DFH=1/2*10/3*20=100/3cm² , 再假设大正方形边长为40cm,10/40=CH/(40-CH),DH=2cm,S△DFH=1/2*2*40=40cm² 综上：本题缺少条件，大正方形是个变量，△DFH随着■CEFG的改变而改变，五年级做强人所难，十年级勉为其难,十五年级毫无困难！
用户10xxx48 回复 10-02 02:04
看点赞最多解法，那是正确的。
摩客小志
连接BD，CF，因为两个都是正方形，BD//CF，然后先这样再那样，可以得出阴影面积等于小正方形的一半，得50
油腻大叔 回复 10-03 12:52
看错了，不好意思
傻得有水平 回复 油腻大叔 10-03 13:05
我用质问的口气说话才真不好，抱歉，不应该带情绪的。
仙家奇缘6
10＊10/2=50
傻得有水平 回复 10-19 14:11
要证A、H、E共线很麻烦
用户16xxx48
所有的“正确解法”，都建立在一个关键条件上——B、H、F三点共线。
飞往财务自由
当H上移至D时，面积为0，当两个面积相同时面积为50。答案应该是0-50
飞天男孩979 回复 10-04 23:34
当h上移至d时，小正方形正好是对角线，也就是大直角三角形在小正方形的底角是45°，那么另一个底角也是45°，也就是说这条线也是大正方形的对角线，也就是小正方形右边的一条10厘米的边两个顶点是重合的，你觉得你的假设还能成立吗？
Hjnhw 回复 12-15 22:36
H只能无限接近D，不会重合，假设HD重合的话，BEF就形成了一个45度的等腰直角三角形，BC+CE=EF，这与大正形矛盾。
尾生
令EF=a，三角形BCH与三角形BEF相似，则BC/CH=BE/EF，CH=BC*EF/BE=10a/(10+a)，DH=CD-CH=100/(10+a)，S红=DH*(10+a)/2=50
芯大
好奇怪啊，H在D下面是50，H在D上面也是50，DH重合为0。只要不重合50。变成0或50，而不是0到50，好奇怪。只是动一下，变量这么大。
Hjnhw 回复 12-15 23:38
奇怪的是你吧，EF<BE那么∠FBE小于45度，H点只能在D点下面，怎么跑到上面的？
用户10xxx48
小学做法如图，答案50c㎡
说我就来
考察的是蝴蝶模型。不过可以利用极限思维，让H点和D点或者C重合，即可轻松得出为50。
godyear 回复 12-21 00:17
小学
帅老师
拉两次窗帘，第一次A拉到B（AB∥CD，左边三角形变成BDH，跟右边三角形合成一个三角形BDF。第二次，F拉到C（FC∥DB），三角形变成了BCD，所以面积是50
嗄呗
连接BD和CF，易证：BD∥CF，易得：S△DHF=S△BCH，S红=10²/2=50。
嗄呗 回复 10-02 16:53
另外一个正方形不管怎么变， H都会在CD上。(平行线判定定理：同位角相等(45⁰)。)
油腻大叔 回复 嗄呗 10-03 12:52
实在不好意思，看错了[笑着哭]
韩雪松
补全，延长BA、FG交于O，设右侧正方形边长为A，然后用BFO-BGD-ADGO-ABH，即可得。
1100032
小编，这题一点都不严谨，有点丢数学老师的脸。
用户10xxx48 回复 10-02 02:04
重新学小学数学即可。
1100032 回复 用户10xxx48 10-02 07:32
你读过小学吗？
花靓Kan
讲一大堆搞到咁复杂，哎，，， 连接DE,HE，DHF=DHE，，， ADE=10*10/2=50
望远镜 回复 11-09 16:06
厉害
等酒香醇 回复 10-19 13:56
怎么证明AEH三点共线？
司辰
小学有点难。梯形两腰三角形面积相等
用户10xxx48
小学解法如图所示，答案50
用户17xxx54
大正方形无限大时，结果也无限大啊！
九天
连接bd和cf，在梯形bdfc中，S△bhc＝S△dhf，所以S阴影面积为小正方形的一半即50。
用户10xxx20
这些小学5年级的题目，直接将大正方形的边设成20就好，这样小学生才可以做。关键要理解无论大正方形是多大，都不影响结果，那么仁义代入一个最容易算的大正方形边长就好。
用户10xxx77
猜一个，50
流水哥哥
应该是延长BA和FG到点O,或者延长AD到EF于点Z,再按照比例和未知数运算，反正这题目我看了都不想算，更别提小孩了。
人的价值绝不在于名望身份和地位
你看DHF和BHC什么关系，就知道咋回事了
007
拉窗帘原理
失落的秋天
50
成林十八木
画两个正方形面积一样的就能发现问题，对角线相连，切分两边面积一样。 这样右边的正方形增大，右侧阴影面积变细长，直到对角线完全切左侧正方形右顶点，完成左侧正方形对分。 由此对角线切割阴影面积是一个常数，半个小正方形面积。
成林十八木 回复 喂，是你 12-16 07:46
你可以画下看看，这个就是可以放大缩小看到规律
喂，是你 回复 12-16 06:52
当大正方面积是小正方形10倍的时候呢？
独往独来
不会
FEI
假设该题有唯一解，那么，大正方形的大小不会影响阴影面积大小。再假设大正方形和小正方形一样大，即DG=0，大正方形边长为10，可知，阴影部分是底边20高5的三角形，得面积50。同理，假设大正方形面积为0，则阴影为小正方形一半，50。
FEI 回复 12-16 07:30
小学五年级的题目，何必搞那么复杂，不用算都知道结果一样。
喂，是你 回复 FEI 12-16 15:33
大胆假设，小心求证。怎能自欺欺人！
路漫漫
连接BD和AC，根据同底等高面积相等，可以得出S△ADH＝S△BDH,S△BDF＝S△BDC＝½×10×10＝50
用户14xxx91
50，用相似的方法不难算，不过超纲了
用户13xxx77
五年级的题10*10/2=50，把右三角形顶点挪至下方，则与原来组成一个大三角形
亚楼
利用蝴蝶原理，把大正方形那个阴影面积折腾到小正方形里，面积为小正方形一半，为50cm²。
godyear 回复 12-21 00:17
小学
用户11xxx92
等积模型，50
用户12xxx34
用bch和bef相似，就能得到阴影面积底乘高的2倍，
Locky
五年级[笑着哭][笑着哭][笑着哭]
明月照人
拉窗帘，50
用户17xxx19
蝴蝶模型，50
godyear 回复 12-21 00:17
小学
zhangzhu
如果是填空/选择题，可以设右边正方形边长为0，瞬间可得结果。
风清
每次遇到这种题，我都着急忙慌的点进来找答案，先看题研究半天，然后看评论区解答，然后意犹未尽的退出去。因为我看不懂。。。打小数学就没及格过，尤其是几何[捂脸哭]
Sagittarius
dhf=bch,bch+adh=50
用户10xxx48
小学做法如图，答案50c㎡
godyear 回复 12-21 00:16
超纲了
用户12xxx66
题目得加个条件BHF在同一条直线上，不然只能解出0到无限大。
Hjnhw
设大正方形边长为a，CH/EF=BC/BE，代入a得CH=10a/(10+a)，DH=10-CH=100/(10+a)，阴影面积为三角形ADH+FDH=0.5*10*DH+0.5*a*DH=0.5*10*100/(10+a)+0.5*a*100/(10+a)=50
点
链接BD得到同底（DH）等高三角形。既BDF面积为阴影面积。然后同底（BD）三角形BDC面积为阴影面积既50。因为BD平行于CF,垂直于平行线内的线段相等，所以BDF与BDC同底等高。
不知不知
50