分子动力学模拟计算热导率优缺点

相比其他常用计算热导率方法（常用计算方法的简介请参见），分子动力学计算方法能够计算更大的体系，计算原子数通常在数百到数十万个范围，尺度在纳米到微米区间。分子动力学模拟包含了声子与声子之间的各阶散射，能够更加真实地模拟声子间的相互作用。但是该方法需要用到经典作用势，计算热导率的准确程度与所用的势函数类型及参数密切相关。该方法也不适合用于低温，通常要求体系的温度要高于模拟物质的德拜温度，如果温度过低，需要考虑对温度进行量子修正。

平衡态分子动力学

分子动力学计算热导率的常用方法有平衡态分子动力学（EquilibriumMolecularDynamics,EMD）和非平衡态分子动力学(NonequilibriumMolecularDynamics,NEMD)。两种体系在计算过程中都处于稳态（体系的温度分布不随时间发生变化），其中，前者不存在温度梯度，通过原子间的微热流来实现热量交换，继而由统计力学原理来得到热导率。后者存在一个稳定的温度梯度，类似于实验中直观的热导率测量方法，所以又被称为直接法（Direct method）,我们在后面的文章会详细介绍采用NEMD计算热导率的方法，在这里略去不表。

EMD的优势&劣势：尺寸效应相对较小，理论上采用周期性边界条件可以实现计算无限大的体系。但是该方法要得到收敛的热流需要较长的弛豫时间，需要比较大的计算量。

具体地，EMD方法计算热导率由如下的Green-Kubo公式得到：

其中，是热导率张量，别代表三个方向，V是模拟体系的体积，是玻尔兹曼常数，T表示模拟体系温度，表示热流自相关函数，尖括号表示对热流自相关函数进行系综平均，t表示热流自相关函数的积分上限，τ表示相关时间。对于三维各项同性材料，热导率张量的非对角张量一定为零，我们通常会计算三个方向的热导率数值，然后取平均得到最终的热导率数值。对于一维结构（单链、纳米线等）只需要对某一个方向的热流自相关函数进行积分，对二维结构，可以分别计算两个面内两个方向的热导率然后取平均。

我们通常在微正则系综（NVE）下记录热流，此时，系统相当于是一个孤立体系，没有外界干扰。在正式记录热流之前，需要对结构进行充分弛豫以得到优化好的结构。前期优化不充分可能会导致能量、温度、压强等物理量在热流记录阶段出现异常，所以在记录热流的过程中可以输出这些物理量帮助自己做出判断。最终得到的热流自相关应该在0附近做很小的震荡变化，因为相关时间越长，初始的热流信号与该时刻的热流信号的差异会越大。热流自相关积分得到的热导率也应该是随着积分时间的增加而达到收敛。

计算时需要对时间步长、热流取样间隔、相关时间步、总的记录热流时间步等参数做收敛性测试。通常最终的热导率计算结果需要使用不同的初始速度计算多次，然后取平均值。

以下给出LAMMPS采用EMD方法计算固体氩晶格热导率实例

1# sample LAMMPS input script for thermal conductivity of liquid LJ` 2# Green-Kubo method via compute heat/flux and fix ave/correlate` 3# settings` 4variable x equal 10 `#模拟体系X方向长度` 5variable y equal 10 `#模拟体系Y方向长度` 6variable z equal 10 `#模拟体系Z方向长度` 7variable rho equal 0.6 `#固体氩晶格常数` 8variable t equal 1.35 `#模拟体系温度` 9variable rc equal 2.5 `#截断半径` 10variable p equal 200 `# 热流相关长度` 11variable s equal 10 `# 热流取样间隔` 12variable d equal $p*$s `# 输出热流自相关函数间隔` 13`# setup problem` 14units lj `#模拟体系采用的` **单位**`（具体各个物理量的单位查LAMMPS手册）` 15timestep 0.005 `#时间步长0.005tau` 16atom_style atomic `#定义模拟体系原子所具有的属性` 17lattice fcc ${rho} `#定义晶格类型和晶格常数` 18region box block 0 $x 0 $y 0 $z `#模拟体系大小` 19create_box 1 box `#创建模拟体系box` 20create_atoms 1 box `#创建模拟体系原子` 21mass 1 1.0 `#给定原子质量` 22velocity all create $t 87287 `#给定特定温度下的初始速度，其中87287是随机数，可以任意取值` 23pair_style lj/cut ${rc} `#定义原子间作用势和截断半径` 24pair_coeff 1 1 1.0 1.0 `#势函数参数值` 25neighbor 0.3 bin `#定义近邻原子` 26neigh_modify delay 0 every 1 `#创建近邻原子列表` 27# 1st equilibration run 28fix 1 all nvt temp $t $t 0.5 `#NVT系综弛豫` 29thermo 100 `#每100步输出一次默认参数` 30run 1000 `#跑1000步` 31velocity all scale $t `#调整体系温度以达到给定值` 32unfix 1 33# thermal conductivity calculation 34reset_timestep 0 `#重新设置时间步为0` 35compute myKE all ke/atom `#计算每个原子的动能` 36compute myPE all pe/atom `#计算每个原子的势能` 37compute myStress all stress/atom NULL virial `#计算每个原子的应力张量` 38compute flux all heat/flux myKE myPE myStress `#计算热流` 39fix 1 all nve `#NVE系综下记录热流` 40fix JJ all ave/correlate $s $p $d & `#计算热流自相关函数并输出到指定文件` 41 c_flux[1] c_flux[2] c_flux[3] type auto & 42 file profile.heatflux ave running 43variable scale equal $s*dt/$t/$t/vol 44variable k11 equal trap(f_JJ[3])*${scale} `#对热流自相关函数做积分` 45variable k22 equal trap(f_JJ[4])*${scale} 46variable k33 equal trap(f_JJ[5])*${scale} 47thermo $d `#输出变量间隔` 48thermo_style custom step temp v_Jx v_Jy v_Jz v_k11 v_k22 v_k33 `#自定义输出物理量类型` 49run 100000 `#跑100000步，可以得到10组热流数据以及热导率数据，采用最后一组数据` 50variable kappa equal (v_k11+v_k22+v_k33)/3.0 `#对三个方向热导率做平均` 51print "running average conductivity: ${kappa}" `#在屏幕上输出热导率数值`

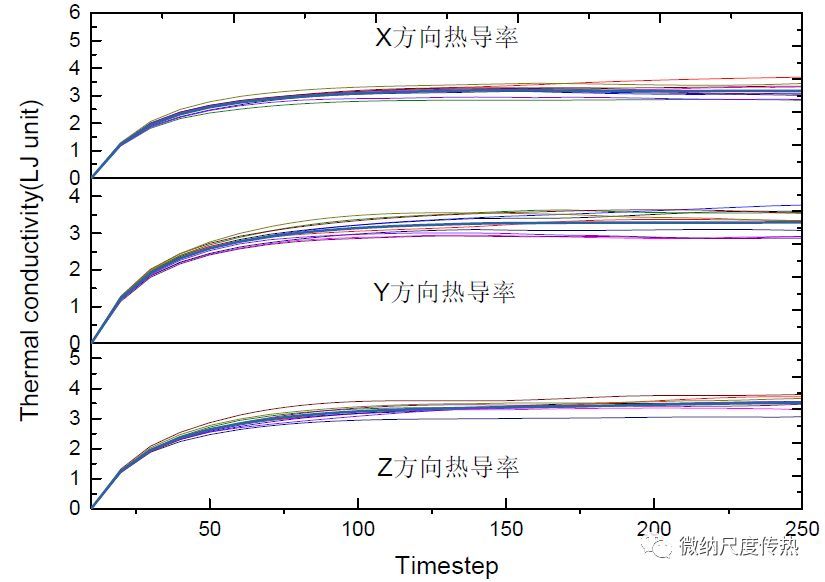
下图为笔者采用上述LAMMPS脚本计算得到的10组热流自相关函数和热导率结果：

本文由邵成和鲍华编辑