
在数学的世界里,某些符号具有超乎寻常的力量。π,这个表示圆周率的符号,不仅广为人知,还常常成为数学趣闻的主角。
而另一个不容忽视的符号则是e,一个看似简单的字母,却承载着深远的意义。
e不仅出现在自然对数中,还深刻影响着微积分、复数、金融等众多领域的计算和推理。
它如同数学的“幽灵”,无处不在。那么,这个神秘的e是如何诞生的?
又是为了解决什么问题?
让我们走进它的历史与本质,揭开e背后的谜团。
01 e的起源:一次追求“增长”的旅程
要了解e的诞生,我们必须回到17世纪的欧洲。
那时,数学家们正试图解决一个重要的实际问题:复利增长。
复利这一概念如今在金融领域耳熟能详,但在当时,这还是一个复杂且充满挑战的课题。
假设我们将一定量的钱存入银行,每年按照固定的利率计算利息。
利息会加入本金,下一年利息就会基于新的本金继续增加,这就是复利的原理。
而关键问题在于,如果利息是逐年结算的,我们可以轻松计算增长的金额,但如果利息不断加速增长呢?
也就是说,如果利息是“连续”地计算,增长的速度会变成什么样子?
这时候,一个重要的问题出现了:当计算周期趋向无穷小(即几乎是连续)的情况下,最终的增长是多少?
这正是数学家们尝试解答的问题,而答案便指向了一个常数,这个常数就是后来的e。
02 逐步逼近:e的发现之路
为了更直观地解释,我们来看一个简单的例子。
如果我们有1元钱,年利率是100%,假设银行按以下方式计算利息:
- 如果每年只结算一次,最终你会有2元。
- 如果每半年结算一次,每次增长50%,那么年末你会有(1+0.5)²=2.25元。
- 如果每季度结算一次,每次增长25%,你将有(1+0.25)⁴=2.441元。
- 如果我们继续增加计算频率,每月一次,每天一次,甚至每秒一次,你会发现最终的结果在慢慢逼近一个固定的数字。
这就是数学常数e的最初发现,它代表着当增长变为连续时,复利的极限值。
03 e的数学定义
在数学上,e可以用一个极限公式精确定义:

这意味着,当n变得越来越大,公式右边的表达式会趋向一个常数,而这个常数就是e。
它的近似值为2.718281828459,这个数值无理数,无限不循环小数,像π一样,e也具有无穷尽的特性。
虽然e最初是为了解释复利增长而提出的,但它的影响远不止金融领域。让我们看看这个常数在其他方面的广泛应用。
当然,微积分是理解变化和动态过程的强大工具,而e在其中扮演了至关重要的角色。
特别是在微积分的分支——微分和积分中,e的自然对数函数ln(x)具有令人惊奇的特性。
例如,函数f(x)=e^x是唯一一个其导数与自身相等的函数,这使得它在解微分方程和处理变化率问题时尤为重要。
04 概率与统计中的出现
在统计学中,正态分布被认为是最常见的概率分布之一,而它的公式中也包含了e。正态分布的概率密度函数为:
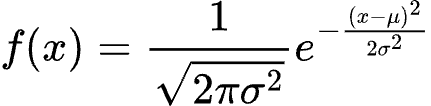
e的存在确保了正态分布的对称性和特定的曲线形状,它帮助我们理解随机事件的分布方式。
另外,e的另一个神奇之处在于它与复数的结合产生了欧拉公式,这被广泛认为是数学中最美的公式之一:
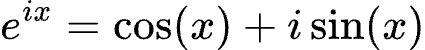
这个公式不仅将指数函数与三角函数联系起来,还将数学中的四大重要常数:e、π、i(虚数单位)和1,神奇地结合在了一起。
欧拉公式在物理学、工程学等领域有着深远的应用,尤其在波动和振动的研究中。
05 为什么选择“e”作为符号?
既然e如此重要,那为什么会选择“e”作为它的符号呢?
这个问题没有明确的答案,但有几种可能的解释流传下来。
首先,“e”可能是为了纪念莱昂哈德·欧拉,这位瑞士数学家在18世纪对e进行了深入研究,并将其广泛应用于各个数学领域。
欧拉不仅发现了e的众多性质,还在数学史上留下了无数伟大的贡献。尽管e这个符号的使用早于欧拉,但正是在他的推动下,e的广泛应用得以普及。
另一种解释是,“e”可能代表exponent(指数),因为e最常与指数函数结合使用。在指数函数中,变量的增长遵循一种指数律,而e正是这种增长的基础。
数学常数e的诞生看似源于金融中的实际问题,但它的魅力远超出简单的利息计算。
它跨越了金融、统计、物理等多个领域,为我们提供了理解变化和增长的工具。
当我们凝视这神秘的2.71828时,它仿佛告诉我们:数学不仅仅是数字和符号的堆积,更是一种理解世界的方式。正如π是理解圆的钥匙,e则是开启增长、变化与平衡的门。
总结
无论是计算复利增长,还是解答微积分中的复杂问题,e始终展现出它无穷的力量与魅力。
如今,e依旧在科学前沿发挥作用,特别是在现代金融、工程和数据科学中。
下次当你听到有人提到e这个符号时,希望你能想起它背后蕴含的深厚历史,以及它所承载的数学之美。
