群论（Group theory）是代数学的一个分支，研究抽象代数系统（群）的性质和结构。群论的发展历史可以追溯到19世纪初，不过关于群的一些雏形思想在此之前已经出现。以下是群论发展的一些重要历史节点：

1770年代：法国数学家拉格朗日（Joseph-Louis Lagrange）研究置换在解多项式方程过程中的作用，为群论的产生铺垫了基础。

1800年代初：意大利数学家鲁菲尼（Paolo Ruffini）和挪威数学家阿贝尔（Niels Henrik Abel）证明了五次及以上的一般多项式方程无法用根式求解（阿贝尔-鲁菲尼定理）。这一成果暗示了群论在解决此类问题中的潜在价值。

1830年代：法国数学家伽罗瓦（Évariste Galois）引入了伽罗瓦群的概念，并创立了伽罗瓦理论。伽罗瓦理论研究多项式方程的根的对称性，以及如何利用群的性质来判断多项式方程是否可以用根式求解。伽罗瓦的工作奠定了群论的基础。

1850年代：英国数学家凯莱（Arthur Cayley）和德国数学家雅可比（Carl Gustav Jacob Jacobi）分别研究了置换群的性质，进一步推动了群论的发展。

1870年代-1880年代：德国数学家费尔班克斯（Ferdinand Frobenius）和李群（Sophus Lie）分别对有限群和连续群进行了系统性的研究，为群论的分类和结构理论奠定了基础。

20世纪初：德国数学家朗兰兹（Emmy Noether）和瑞典数学家维尔纳（Hermann Weyl）等人将群论应用到抽象代数、数论和物理学等领域，进一步拓展了群论的应用范围。

在群论中，伽罗瓦群和辫群是两个独特且具有丰富应用的群，它们为我们揭示了许多自然界和数学之间深刻的联系。本文将重点介绍伽罗瓦群和辫群的基本概念、性质以及在数学和物理学中的应用。

伽罗瓦群是群论（Group theory）在数学中的一个重要应用，特别是在解决多项式方程的领域。

给定一个具有有理系数的多项式函数f它的分裂域（splitting feld）就是包含所有有理数和f的所有的根的最小域。f的伽罗瓦群则是分域的所有自同构的群。每一个这种自同构都会把的根加以排列，所以伽罗瓦群可以看作所有这些根的置换群的子群。伽罗瓦群的结构和性质与多项式的可解性密切相关。特别是伽罗瓦群可以用来证明并非所有多项式都可以用根式来解出。这个定理，虽然看起来已经是一大奇观，却并不是伽罗瓦群的仅有的应用，它们在现代的代数数论中起了中心的作用。

上面提到几个概念，我们分别看下：

分裂域

域（Field）是数学中的一个基本概念，特别是在代数学领域。域是一个集合，这个集合中的元素可以进行加法、减法、乘法和除法（除数不为零）四种运算，并且满足一定的代数性质。一个域F必须满足以下性质：

封闭性：对于任意的a和b属于F，它们的和（a+b）、差（a-b）、积（a×b）也都属于F。如果b≠0，它们的商（a/b）也属于F。

结合律：对于任意的a, b, c属于F，加法和乘法运算满足结合律。即 (a+b)+c = a+(b+c) 和 (a×b)×c = a×(b×c)。

交换律：对于任意的a, b属于F，加法和乘法运算满足交换律。即 a+b = b+a 和 a×b = b×a。

存在逆元：对于任意的a属于F，存在加法逆元（相反数）-a 和乘法逆元（倒数）1/a（当a≠0时），使得 a+(-a)=0 和 a×(1/a)=1。

满足这些性质的集合称为域。常见的域包括有理数域Q（所有分数的集合）、实数域R（实数的集合）和复数域C（复数的集合）。此外，还有有限域（有限个元素的域）和函数域（函数的集合）等。

分裂域与多项式方程的解有密切关系，它提供了一个环境，使得多项式方程可以完全分解为线性因子。

给定一个多项式方程f(x) ∈ F[x]（表示多项式f(x)的系数都在F中），其中F是一个域，分裂域是F的一个代数扩张K，满足以下两个条件：

f(x)在K[x]中可以完全分解为线性因子的乘积，即f(x)可以表示为f(x)=(x - a1)(x - a2)...(x - an)，其中a1，a2，...，an属于K。

K是满足条件1的最小扩张，也就是说，任何包含F的并且使得f(x)分解为线性因子的域都包含K。

换句话说，分裂域是一个包含了多项式方程所有根的最小代数扩张。分裂域的概念在伽罗瓦理论中非常重要，因为它与伽罗瓦群有密切联系。

代数扩张（algebraic extension）是代数学中的一个概念，用于描述从一个域扩大到包含更多元素的另一个域的过程。给定一个域F，代数扩张是指一个包含F的更大域K，使得K中的每个元素都是F上的一个代数元。

自同构

自同构（automorphism）是代数学中的一个概念，主要用于描述一个数学结构到其自身的同构映射。在不同的数学结构中，自同构可能有不同的定义，但通常来说，它是一种保持结构性质的双射映射（一一对应）。对于域F，域自同构是指一个从F到其自身的双射映射φ：F→F，它满足以下性质：

加法和乘法保持性：对于F中的任意元素a和b，有φ(a+b) = φ(a) + φ(b)以及φ(a×b) = φ(a)×φ(b)。

单位元和零元保持性：φ(1_F) = 1_F 和 φ(0_F) = 0_F，其中1_F和0_F分别是F的乘法单位元和加法零元。

类似地，在其他代数结构（如群、环、向量空间等）中，自同构也是保持相应结构性质的映射。自同构在研究数学结构的内在对称性和性质方面起着关键作用。

置换群

置换群（Permutation group）是一个关于集合上置换的群。置换是一个集合上的双射映射，将集合的元素重新排列。置换群是这些置换按照函数复合运算形成的群。在置换群中，群运算是函数复合，即两个置换按照顺序执行。置换群满足群的所有性质，包括：

封闭性：两个置换的复合仍然是一个置换。

结合律：对于任意的置换a, b和c，有(a ∘ b) ∘ c = a ∘ (b ∘ c)。

单位元：存在一个恒等置换，记作id，它不改变任何元素的位置，即对于A中的任意元素x，有id(x) = x。对于任意的置换a，有a ∘ id = id ∘ a = a。

逆元：对于每个置换a，存在一个逆置换a^(-1)，使得a ∘ a^(-1) = a^(-1) ∘ a = id。

我们来说明一个简单的置换群的例子。考虑一个有3个元素的集合A = {1, 2, 3}。我们可以列出A上所有可能的置换：

恒等置换（Identity permutation）：id = (1, 2, 3)。这是一个不改变元素位置的置换，即id(1) = 1, id(2) = 2, id(3) = 3。

置换σ1：(1, 2, 3) → (2, 1, 3)。这个置换交换了1和2的位置，即σ1(1) = 2, σ1(2) = 1, σ1(3) = 3。

置换σ2：(1, 2, 3) → (1, 3, 2)。这个置换交换了2和3的位置，即σ2(1) = 1, σ2(2) = 3, σ2(3) = 2。

置换σ3：(1, 2, 3) → (2, 3, 1)。这个置换是一个循环置换，即σ3(1) = 2, σ3(2) = 3, σ3(3) = 1。

置换σ4：(1, 2, 3) → (3, 2, 1)。这个置换交换了1和3的位置，即σ4(1) = 3, σ4(2) = 2, σ4(3) = 1。

置换σ5：(1, 2, 3) → (3, 1, 2)。这个置换是一个循环置换，即σ5(1) = 3, σ5(2) = 1, σ5(3) = 2。

现在，我们可以构造一个对称群S_3，包含这6个置换。群运算是函数复合，即按顺序执行两个置换。例如，σ1 ∘ σ2 表示首先应用σ1，然后应用σ2。具体计算如下：

σ1 ∘ σ2 = (2, 1, 3) ∘ (1, 3, 2) = (1, 3, 2)

这是因为σ1(σ2(1)) = σ1(1) = 2，σ1(σ2(2)) = σ1(3) = 3，σ1(σ2(3)) = σ1(2) = 1。

对称群S_3满足群的所有性质，包括封闭性、结合律、存在单位元和逆元。例如，σ1的逆元是它自身，因为σ1 ∘ σ1 = id。对称群S_3在这种情况下有6个元素，即3! = 6。

举例说明伽罗瓦群

让我们通过一个简单的例子来说明伽罗瓦群的概念。考虑一个三次多项式方程：f(x) = x^3 - 2。我们可以找到这个方程的三个根：

其中ω是单位圆上的一个立方根，ω = e^(2πi/3)，ω^3 = 1。

我们注意到，这三个根之间存在一个置换关系，即将ω替换为ω^2（或者ω^4）时，我们可以得到一个新的根。例如，将ω替换为ω^2得到：

这种关系产生了一个伽罗瓦群，我们可以将其视为对称群S_3的一个子群。为了构造伽罗瓦群，我们需要考虑所有可能的置换，它们在有理数域Q上保持多项式系数不变。在这个例子中，我们有以下两个置换：

恒等置换：id = (α, β, γ)。这个置换保持所有根不变。

置换σ：(α, β, γ) → (α, γ, β)。这个置换交换了根β和γ，即σ(α) = α, σ(β) = γ, σ(γ) = β。

这两个置换构成了伽罗瓦群G，G = {id, σ}。可以验证这个群满足封闭性、结合律、存在单位元和逆元等群的性质。在这个例子中，伽罗瓦群是一个很小的群，只包含两个元素。然而，在其他更复杂的代数方程中，伽罗瓦群可能包含更多的置换，甚至可能是无限的。

辫群，顾名思义，是与辫子结构相关的群。它描述了一种特殊的交换和置换关系，具有丰富的拓扑性质。

取两个平行的平面，每一个各钻 n 个孔，依次将它们编号为 1到n。然后牵根绳子，从一个平面上的一个孔牵到另一平面的一个孔，但不能让两根绳子穿过同一个孔，这样就得到一个 n辫。把这两个平面立起来从侧面看过去，就得到它们的2维投影，而两个3辫的2维投影就与纽结图示相似，可见下图，

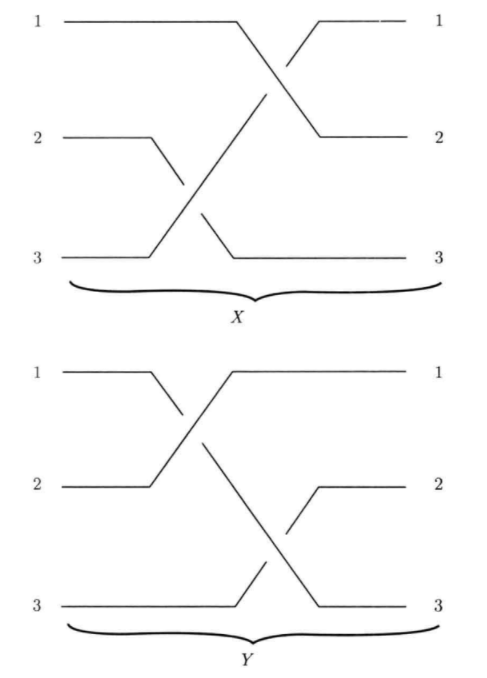
两个3辫

这个图示暗示了我们坚持把绳子从左穿到右，而且不许“折转”，所以，打结的绳子是不许可的。

在此，在辨的描述上有一定的自由：只要把绳子的端点固定，不能拉断绳子，也不准它们互相穿过，除此以外，可以拉伸、压缩、弯曲或者在3 维空间里移动得到的

都算是同样的辫。这种“相同性”是一个等价关系，称为辫的同痕（isotopy）。辫可以组合如下：把两个放在一起使同编号的孔毗邻地位于一个公共（居中）的平面上，把 穿过居中平面的同一个孔的两根绳子连接起来，再把居中的平面抽走。下图画的就是上图的两个辨X与Y的复合，记为 XY

在这样的复合之下，n辫构成一个群，称为辫群，记作B_n。在我们的例子中，

把连起来的绳子“拉紧”，立刻可以看出 XY 同痕于下图上的平凡辨，其作用就是恒等元.

作为一个群，B_n是由（σ_i），1≤i≤n-1生成的，σ_i是由平凡辫把第i根绳子穿到第i＋1个洞,同时把第i＋1根绳子穿到第i个洞而生成的。读者可以看到，σ_i与生成{1，…，n}的置换群S_n的相邻元的对换（transposition）（即将第i个元与第i＋1个元交换位置）的相似性。事实上，任意的辫必定按照以下的规则决定一个置换：

生成元σ_i

如果只关注绳子端点的变化，而忽略其他一切，就会得到一个满射B_n→S_n，把σ_i映为对换（i，i＋1）。但是，这不是一个同构，因为B_n是一个无限群，事实上，σ_i的阶数就是无穷，而对换（i，i＋1）平方以后就给出恒等元。阿廷在1925年的著名论文《辫的理论》（Theorieder Zopfe）中就证明了，B_n中的乘法完全由以下关系决定：

这些关系后来发现在统计物理中很重要，称为Yang-Baxter方程式。

在由生成元和关系所定义的群中，要决定生成元的任意的字（word）是否为恒等元一般是很困难的事。没有一个在各个情况下都一致可用的方法。对于B_n，阿廷用"梳辫子"的方法几何地解决了这个问题。另一种由Garside提出的代数方法决定了 B_n的两个元何时为共轭的问题。

关于这些问题是否可判定，以及在许多其他方面，辫群都展现了和线性群有密切的亲和关系。虽然这种相似性暗示了应该可以证明辫群其实就是线性群。但是这个问题多年一直没有解决，直到2001年才由Bigelow给出了证明，Krammer也独立地得到了证明。

这里描述的群，严格地说只是平面上的辫群，打孔的对象是平面。其他的辫群还出现在别的地方，而且时常令人大吃一惊。它与统计物理的联系上面已经提到了，它们也在代数几何里出现：代数曲线去掉例外点，就是打了孔。这样、虽然辫的来源在拓扑学，却在其他领域里也引人注目，例如在初看起来纯粹是代数问题的“构造伽罗瓦理论”中。

最后

在本次讨论中，我们了解了伽罗瓦群和辫群这两个重要的代数结构。伽罗瓦群在解析代数方程根之间的关系方面发挥着关键作用，特别是在判断代数方程是否可以通过根式求解。伽罗瓦理论是现代数学中的一个重要支柱，其影响力远超数学领域本身。

辫群则描述了拓扑学中一类具有丰富结构和对称性的对象——辫子。辫群在拓扑学、代数和数学物理中都有广泛的应用，提供了一种强大的工具来理解各种数学和物理系统中的对称和不变性。

尽管伽罗瓦群和辫群之间没有直接的联系，但它们都在各自的领域展示了数学中对称性和结构的巧妙组织。这两个概念都是数学家们在理解现实世界中的复杂结构和现象时的关键工具。通过研究伽罗瓦群和辫群等概念，数学家们可以不断地发现新的数学结构和定理，从而拓展我们对数学和现实世界的认识。