行列式是线性代数中的一个重要概念，它为我们提供了一种理解矩阵性质和求解线性方程组的方法。

行列式的概念最早可以追溯到18世纪的法国数学家克莱姆特（Gabriel Cramer）的工作。现今，行列式在科学和工程领域都扮演着举足轻重的角色。了解行列式的基本性质和计算方法，对于研究线性代数和解决实际问题具有重要意义。

考虑一个2×2矩阵

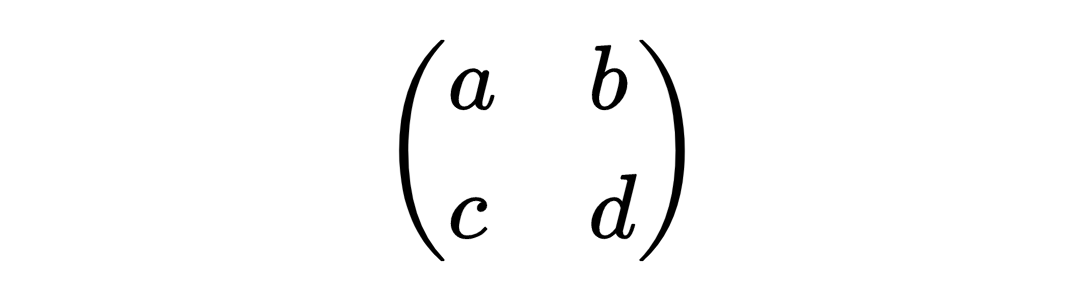
的行列式定义为 ad-bc。一个3×3的矩阵

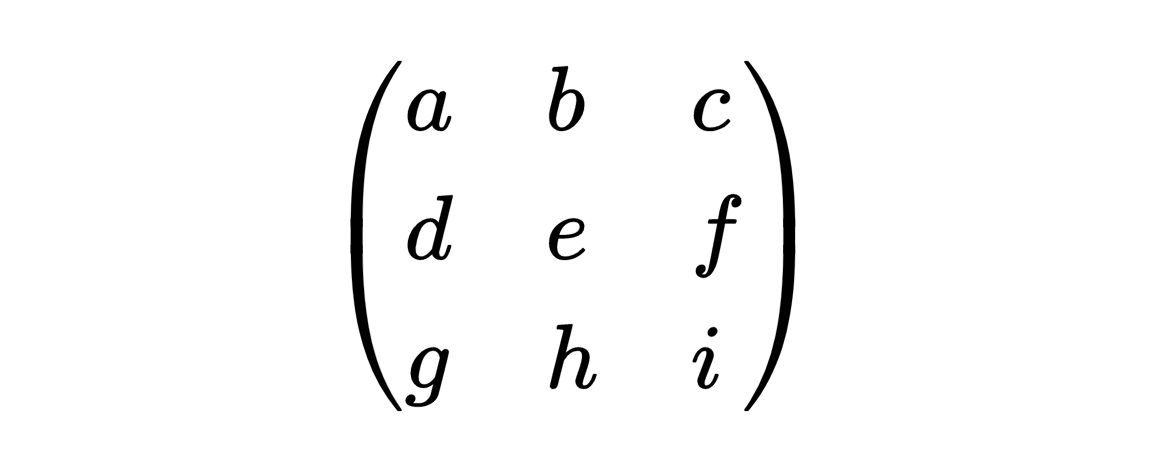
的行列式定义为

这些表达式有什么共同之点，怎样推广，为什么这种推广有意义？

我们从第一个问题开始，先作一些简单的观察。这两个式子都是矩阵的元的乘积之和与差，每一项都包含了矩阵的每一行和每一列的恰好一个元。

把这个定义推广到n×n的矩阵上也是容易的。我们只要取所有的由矩阵的n个元所成的乘积，但这n个元，必须每一行都有一个元，每一列也都有一个元，然后把它们求和或者求差。难就难在哪些乘积要加起来，哪些乘积要减去。为了做这件事，取一个乘积，然后用它来定义集合{1，2，……，n}的一个排列σ如下：对于每一个i≤n，乘积中恰好含有来自第i行的一个元，如果此元属于第j列，就定义σ（i）=j。如果这个排列是偶排列，对这个乘积就附上加号，而把它加上；如果是奇排列，就附上负号，而把它减去。这样，作为一个例子，我们来看上面的3×3行列式中的afh这一项。相应的排列是把1变到1，把2变到3，又把3变到2，这是一个奇排列。所以，这一项得到的是一个负号。

我们还要解释一下，为什么乘积的这种特殊的选择和上面定义的负号的取法很重要。理由在于它多少告诉了我们，如果把矩阵看成一个线性变换会有什么效果。 令A为一个n×n矩阵。则A确定了一个由R^n到R^n的线性映射α。A 的行列式则告诉我们这个映射对于体积做了些什么事。更精确地说，若X为R^n的一个子集合，其体积为V，则αX即用α对X作变换的结果，其体积应该是用A的行列式去乘V。把这个结果用符号写成

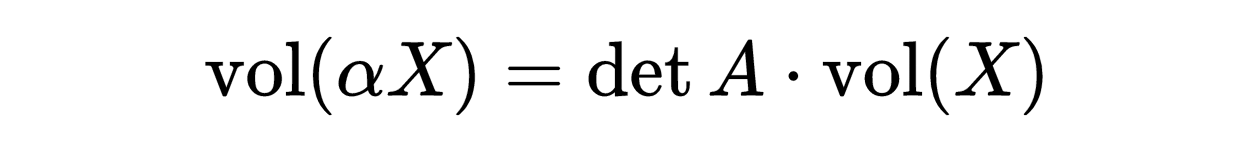
例如考虑2×2矩阵

相应的线性变换是R^2中旋转一个角θ。因为把一个图形作旋转，不会改变其体积，我们会期望其行列式等于1，所以肯定sinθ·（-sinθ）这一项一定加负号，这样会得到

这就是毕达哥拉斯定理。

以上的解释在一个方面有点过分简单化：行列式可以取负值，而体积不会。如果一个矩阵的行列式为-2，就表示这个线性变换既把体积大小增加2倍，又把"里面翻到外面"作了一次反射。

当知道了行列式用体积的解释以后，行列式的许多有用的性质就变得很显然了（然而，这个体积解释本身的正确性却不那么明显了；要建立行列式的理论，需要在别处下功夫）。下面给出三个这样的性质。

令V为一个向量空间，而a：V→V为一线性映射。令v1，…，vn为V的一个基底，而A为α关于这个基底的矩阵。现在再令w1，……，wn为V的另一个基底，而 B为α 关于这另一个基底的矩阵。于是A和B将是不同的矩阵，但是因为它们代表同一个线性映射α，它们对于体积将产生同样的效果。由此可知，det（A）=det（B）。换一个方法来说，行列式是线性映射的性质，而不说它是矩阵的性质。

两个代表同样线性映射的矩阵称为是相似的。可以证明，当且仅当存在一个可逆矩阵P使得

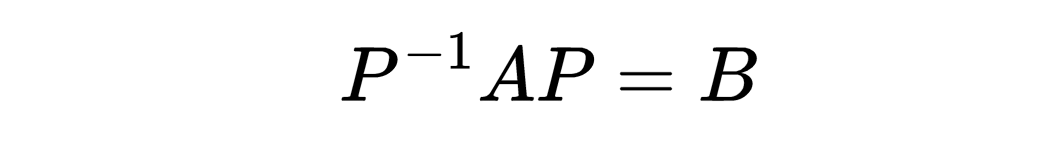
时，A和B为相似。对于一个n×n矩阵P，如果存在一个矩阵Q使得PQ等于n×n恒等矩阵I_n，就有P为可逆，由此还可以得到QP也等于I_n。如果这一点成立，则称Q为P的逆矩阵，并记为P^-1。我们刚才所证明的就是相似矩阵有相同行列式。

若A和B为两个n×n矩阵，并分别代表R^n的线性映射α和β。乘积AB就代表线性映射aβ，就是作了β再继之以α的线性映射。因为作β已经对体积乘上了 det B，再作α又乘上 det A，所以，作线性映射aβ就会把体积乘上了det A·det B。由此可得det（AB）=det A·det B（即乘积的行列式等于行列式的乘积）。

若A是一个行列式为0的矩阵，而B是另一矩阵，则由上面讨论的行列式的乘积性质，AB的行列式也为0。由此AB不可能等于I_n，因为I_n的行列式等于1。所以，一个行列式为0的矩阵不会是可逆矩阵。这个命题的逆也是成立的：一个行列式不为0的矩阵一定是可逆的。所以，行列式给了我们一个矩阵是否可逆的判据。