17世纪最伟大的数学家，皮埃尔·德·费马（Pierre Fermat，1601？-1665），过着繁忙的生活。尽管数学对他而言只是一个爱好，他却在该领域取得了巨大的成就。费马的研究涉及多个方面，包括积分、深奥的物理原理、解析几何、算术和逻辑。

在算术领域，费马占据着举足轻重的地位。他提出了一些关于素数的未解决问题，这些问题至今仍然困扰着数学家。费马认为，有些定理之所以被认为是“重要的”，是因为它们具有深刻的智力价值，并能推动科学发展。

作为纯粹的数学家，费马至少与牛顿不相上下。并且，牛顿的一生有近三分之一时间活在了18世纪，但费马却完全生活在17世纪。再者，牛顿把他的数学主要当做科学探索的工具。而费马则不然，他虽然在将数学应用于科学，但纯数学对他而言具有更强的吸引力。随着笛卡儿在1637年公布了解析几何，数学开始进入现代阶段，而且在其后的很多年里仍然处在这样的初级阶段。

发明微积分使牛顿作为一个纯数学家的声望达到顶点。而费马在牛顿出生前13年，就想出并应用了微分的主要概念。

至于笛卡儿和费马，他们各自完全独立地发明了解析几何，在这个问题上他们旗鼓相当。笛卡儿的主要努力在于各种各样的科学研究，对他的哲学的苦心经营。费马从未像笛卡尔和帕斯卡那样被关于上帝、人类和宇宙整体的哲学探讨所吸引。在解决了他感兴趣的微积分和解析几何问题之后，费马依然能够将剩余的精力投入到他最热爱的消遣——纯数学。正是在这方面，他完成了他最伟大的成就，奠定了数论的基础，并因此赢得了无可争议的声誉。

很快我们将看到，费马与帕斯卡共同创立了概率论的数学理论。如果所有这些一流的成就还不足以让费马在纯数学领域成为他那个时代的王者，那么我们不禁要问，还有谁能做得更多？费马是一个天生的创造者。严格意义上说，他在科学和数学领域属于业余爱好者。然而毫无疑问，他在科学史上成为了最重要的业余爱好者之一。

费马于1601年8月出生在法国博蒙-德洛马涅。他在数论和数学方面的杰出成就，并非源于他所受的教育，因为当时他所取得突破的领域还未被开发，他所学的内容几乎不可能启发他。在他的实际生活中，值得一提的几个事件包括：他30岁时在图卢兹担任晋见接待官；1648年，他成为图卢兹地方议会的议员，并在这个职位上工作了17年；最后，于1665年1月去世，享年65岁。

我们现在扼要叙述一下费马在微积分的发展中所起的作用。在微分学中，与几何学等价的一个基本问题是在给定点上求曲线的切线。这里所说的“连续曲线”是指一条光滑且无间断或突跃的曲线。简单来说，这个问题关注的是如何找到一条直线，它仅在给定的点上与这样一条连续曲线相接触，形成相切的关系。

费马和其他微积分创始人使用几何和物理的直观思考来解决曲线上某点的切线问题。他们的方法是：

在曲线上选择两个点P和Q。

画一条连接P和Q的直线PQ。

在想象中让点Q沿着曲线向点P滑动，直至Q与P重合。

当点Q靠近点P时，连接P和Q的直线PQ会逐渐接近曲线在点P处的切线。当Q与P完全重合时，直线PQ就变成了曲线在点P的切线。这种方法利用了几何直观来解决微积分中的问题。

下一步就是 将几何语言翻译成代数和分析的过程，以求解曲线上某点的切线问题。

首先，设定点P的坐标为(x, y)，点Q的坐标为(x+a, y+b)。

观察图形，可以看出弦PQ的斜率等于b/a。这个斜率可以理解为弦PQ相对于x轴的倾斜程度。

要找到点P处的切线斜率，需要计算当点Q接近点P（即a和b趋近于0）时，b/a的极限值。这个极限值就是切线的斜率。

知道了切线的斜率和点P的坐标，就可以画出切线。

这个过程将几何问题转换成代数问题，从而更容易地求解曲线在某点处的切线。这并不一定就是费马画切线的过程，但是他的过程大体上与上面描述的过程相同。

为什么求解曲线上某点的切线值得关注。动力学中一个基本概念是移动质点的速度。我们可以绘制一个描述质点运动的线（直线或曲线），它展示了质点在单位时间内通过的距离。在这条线上任意给定点处的切线实际上表示质点在该点的瞬时速度。质点运动得越快，切线斜率越陡。实际上，这个斜率衡量了质点在运动路径上任何点的速度。

当将运动问题转换为几何问题时，它实际上变成了在曲线上找到给定点的斜率的问题。还有类似的问题，如求解曲面上的切平面（在力学和数理物理中也具有重要意义）。这些问题都需要用微分学来解决，而我们已经尝试描述了微分学的基本问题，就是在费马和他的继承者面前所呈现的样子。

在中学教育中，学生们通常会学习到这些知识。在绘制函数y=f(x)的图形时，如果图形上有极大或极小点，我们会发现在这些极值点处，切线将平行于x轴，即切线斜率为零。因此，当我们寻找给定函数f(x)的极值时，我们需要解决曲线y=f(x)斜率问题。在找到一般点(x, y)处的斜率后，令斜率的代数表达式等于零，便可找到该极值点的x值。这就是费马在1628-1629年发现的极大极小方法，10年后才把这个方法给了笛卡儿。

费马极值方法在科学中有广泛的应用。例如，在力学中，拉格朗日发现了当某个关于物体位置和速度的函数取极值时，它提供了系统的运动方程，反过来又可以确定给定时刻的运动。在物理学中，有许多类似的函数，每个函数都概括了数理物理学的一个广泛分支。希尔伯特在1916年为广义相对论发现了一个这样的函数。费马将他的极值方法成功应用于光学。值得注意的是，这一特殊发现被证明是从1926年开始发展的新量子理论的基础，特别是在数学方面的波动方程。

费马还发现了通常称为“最小时间原理”的原理。根据这个原理，光线在从点A传播到点B的过程中，会自动选择一条使传播时间最短（极小）的路径。在这个过程中，光线可能会经历反射和折射。折射是指光线在经过不同介质（如从空气进入水中）时发生弯曲。这个原理表明，尽管光线在传播过程中可能经历各种扭曲、转向和反射，但它总会选择一条让从A到B所需时间最短的路径。

费马将解析几何从二维扩展到了三维，这一扩展对于当时的数学家并不显而易见。他还在一个关于曲线分类的基本论点上修正了笛卡儿的理论。虽然两人在费马的切线方法上发生争论，但最终费马获得了胜利，因为他是正确的。有趣的是，尽管长时间没有明确证据表明牛顿了解费马的微积分成果，但在1934年，L·T·莫尔在其关于牛顿的传记中提到了一封信。在这封信中，牛顿明确表示，他从费马的切线方法中获得了微分法的启示。

我们现在转向费马最伟大的工作——数论。希腊人把我们通常认为的“算术”分成了两个单独的部分，即逻辑学和算术。逻辑学是关于计算在一般商业和日常生活中的实际应用；算术就是在费马和高斯意义下的算术，他们力图去发现关于数的一些性质。

算术研究整数之间的相互关系，这在数学中可能是最复杂的问题。为了解决这些问题，数学家不得不发明代数和分析中的深奥的定理。这些看似无用的研究在其他数学领域产生了丰富的应用，与物理世界产生了直接联系。专业代数学家开发了新方法来解决代数方程理论，这些方法直接源于解决费马大定理。

下面要讨论的，在费马的一生中是非常重要的，在数学史上也是如此。考虑一组数3，5，17，257，65537，它们都属于一个特殊类型的“序列”，因为它们都是用同一个简单的过程生成的，

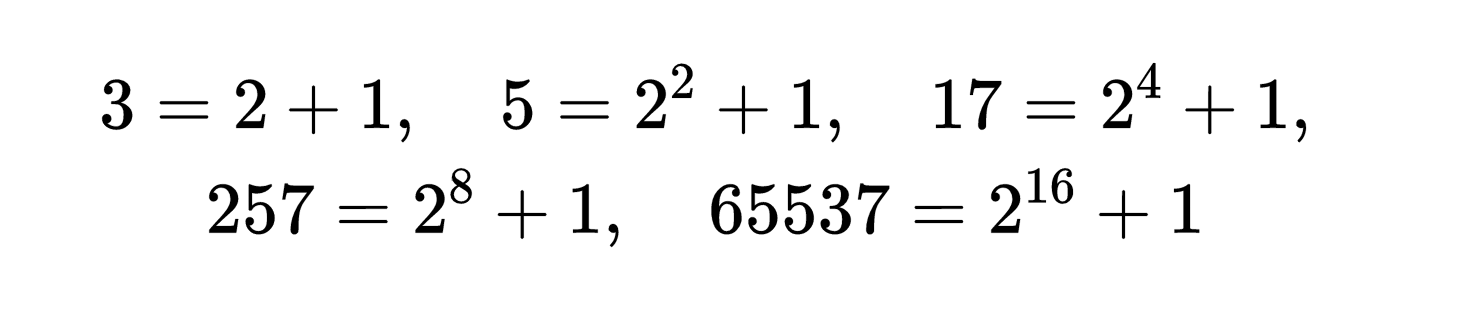
不难发现，这个序列是用下面的公式构成的，

其中n取0,1,2,3……

费马宣称，序列中所有的数都是素数（被称为费马素数）。然而，当n大于4时，费马素数的素数性质就不再成立。例如，F_5 = 2^(2^5) + 1 = 2^32 + 1 = 4294967297，它可以被641整除，因此不是素数。费马素数的研究在数学领域具有重要意义，并为后来的研究提供了基础。

在18世纪末的十年里，数学史上的几个最重要事件之一发生了，这在某种程度上归因于费马素数。其中一件是构造正多边形。古希腊人已经发现如何仅使用直尺和圆规构造正3，4，5，6，8，10和15边形。

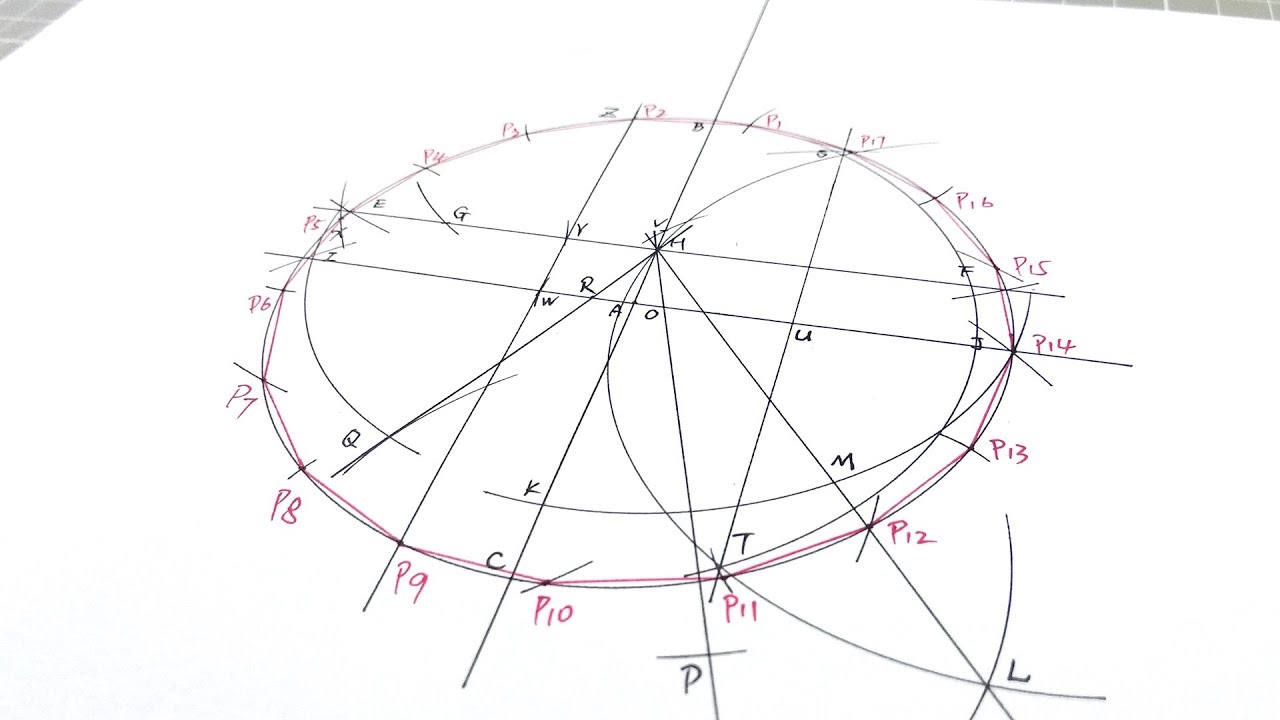
接下来的挑战是用尺规构造正7，9，11，13等边形。许多人尝试过，但没有成功，因为这样的方法是不存在的，只是他们并不知道这是不可能的。在2200多年后，那个在数学和语言学天才迈出了重要的一步。

这位年轻人证明了用直尺和圆规构造奇数边的正多边形是可能的，但只有在边数是费马素数或由不同费马素数相乘得到的数时才可能。因此，正如古希腊人所知，可以构造正3，5和15边形，但不能构造正7，9，11或13边形。正是这个发现，使得这位年轻人选择了数学而非语言学作为他的毕生事业。他的名字叫高斯。

如果n是任意整数，p是任意素数，那么n^p-n可以被p 整除。例如取p=3，n=5，我们得到5^3-5是120；对于n=2，p=11，我们得到2^11-2是2046=11×186。

在数学中，有些定理被认为是“重要的”，而其他一些却被认为是相对不重要的。有几个标准可以用来评估定理的重要性：首先，这个定理应该能应用于数学的其他领域；其次，它应该激发算术或广义数学的研究；第三，它应该在某种程度上具有普遍性。费马定理满足了这些要求：它在数学的许多领域中具有不可或缺的作用，包括群论，群论又是代数方程论的基础；它具有普遍性，因为它描述了所有素数的一个性质，这种普遍性陈述是非常难以发现的。

费马以他的一贯方式陈述了关于n^p-n的定理，但没有给出证明。第一个证明是莱布尼茨给出的。

高斯曾说，

高等算术为我们提供了丰富的有趣事实和真理，这些事实和真理并非孤立存在，它们之间存在着紧密的内在联系。随着我们知识的积累，我们不断在这些事实和真理之间发现新的、有时出人意料的联系。高等算术中的很多定理因为具有以下特性而更具吸引力：具有简单特征的重要命题往往容易通过归纳法发现，但这些特征却很深奥，我们往往需要经过许多徒劳的努力才能找到它们的证明。即使我们确实找到证明，通常也是通过一些复杂且繁琐的过程，而更简单的方法可能需要很长时间才能找到。

高斯提到的这些有趣的事实之一是费马发现的关于数的最美妙的东西：每一个形式为4n＋1的素数是两个数的平方和，并且这种和的形式是唯一的。例如，37被4除有余数1，所以37一定是两个整数的平方和。通过试验，我们发现确实37=1＋36=1²＋6²，并且没有其他两个数x，y能满足37=x²＋y²。

费马也没有留下这个定理的证明。伟大的欧拉在1749年首次证明了这个定理，花了7年时间。

任何玩数字游戏的人很可能会注意到27=25＋2这个奇妙的事实，因为27和25都是某个的数的幂，即

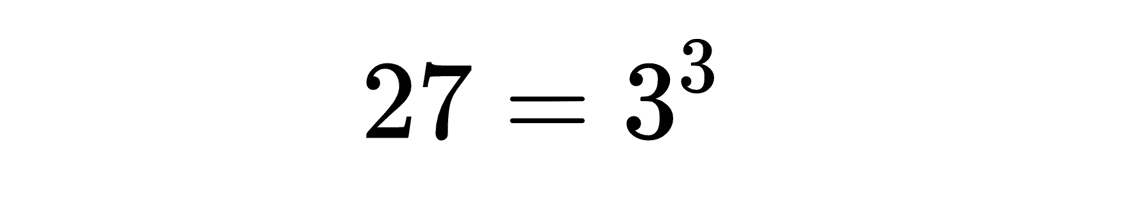
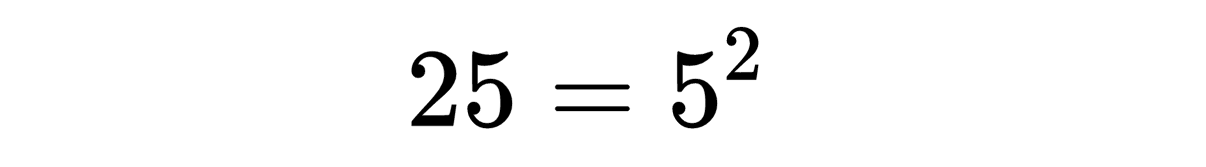
这样我们就观察到，y^2=x^2＋2有一个整数x，y的解；这个解是x=5，y=3。读者现在可以证明y=3，x=5是满足这个方程的唯一整数。这个证明并不容易。事实上，对付这件表面上幼稚的事，比掌握相对论需要更多的天赋。

方程y^2=x^2+2是一个丢番图方程，指一类只寻求整数解的代数方程。与普通代数方程不同，丢番图方程的特点是，我们对这类方程只关心整数解，而不关心实数解或复数解。y=3，x=5这个解是"由检查"看出的；问题的困难在于证明没有其他的整数y，x能满足这个方程。费马证明了没有其他的解，但像通常那样没有发表他的证明。直到他死后好多年，才找到了一个证明。

费马有一个习惯，在读巴歇的《丢番图》时，他把思考的结果简略地记在书页的空白处。空白处不适宜写下证明。这样，费马在评论丢番图的算术的第2卷上第8个问题时，该问题要求方程x^2＋y^2=a^2的有理数解，他写下了如下的话：

反之，不可能把一个数的立方分解成两个数的立方和，把一个数的四次方分解成两个数的四次方的和，或者更一般地说，把大于2的任意次幂的数分解成两个同次幂数的和：我已经发现了（这个一般定理的）一个真正奇妙的证明，但是这个空白太窄了，写不下。

这就是他在大约1637年发现的他的著名的费马大定理。

把这段话用现代语言叙述出来就是：如果n是大于2的整数，则不存在这样的整数x，y，a，使得

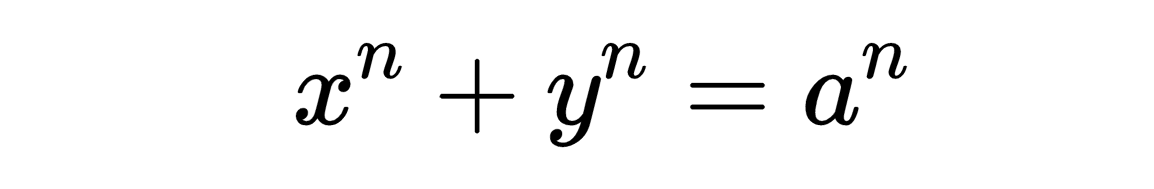
费马本人用他的无穷下降法给出了x^4+y^4=d^4不可解的一个证明。费马有没有弄错的可能呢？

在1994年，英国数学家安德鲁·怀尔斯（Andrew Wiles）成功证明了费马大定理。怀尔斯的证明是通过将费马大定理与其他复杂的数学概念联系起来，如椭圆曲线和模形式。这一证明是一个巨大的成就，不仅解决了一个长期未解的问题，而且还为数学的其他领域带来了深远的影响。

费马大定理在历史上的著名性和证明过程的复杂性使其成为数学领域的一个重要里程碑。