我们通常将π与圆联系在一起。它被定义为圆的周长与其直径的比率。这个定义是相当准确的，数学家们已经知道π好几千年了。古巴比伦、埃及、希腊、印度和中国的数学家们知道如何计算π，并且能够相当精确地得出它的值。公元前200年左右，阿基米德使用几何技术计算出π约为3.14。中国数学家祖冲之在公元500年左右计算出π的七位小数。

π与圆如此紧密的联系并不奇怪，因为这就是人类最初了解到它的方式，也是我们大多数人在学校里首次了解π的方式。但是π有一个更基本的定义，这就是为什么它在更高级的数学中经常出现，而这些数学看起来与圆形几乎没有什么关系。在本文中，我们将看到π的另一面。

手推车和弹簧

假设有一个手推车，它在轨道上运行，通过弹簧连接到一个固定点子：

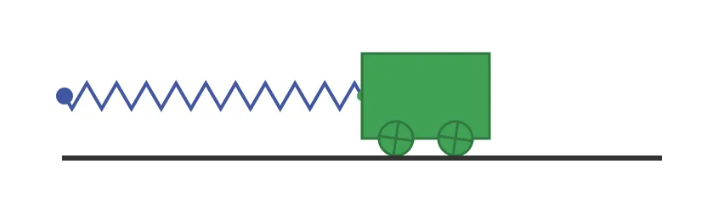
假设手推车重1千克，弹簧每伸展一米就产生1牛顿的力。我们还假设可以忽略摩擦、空气阻力或任何其他效应（如相对论）。

现在弹簧处于张力状态。它以1牛顿的力拉着手推车，如果放开手推车，弹簧会将它拉回固定点：

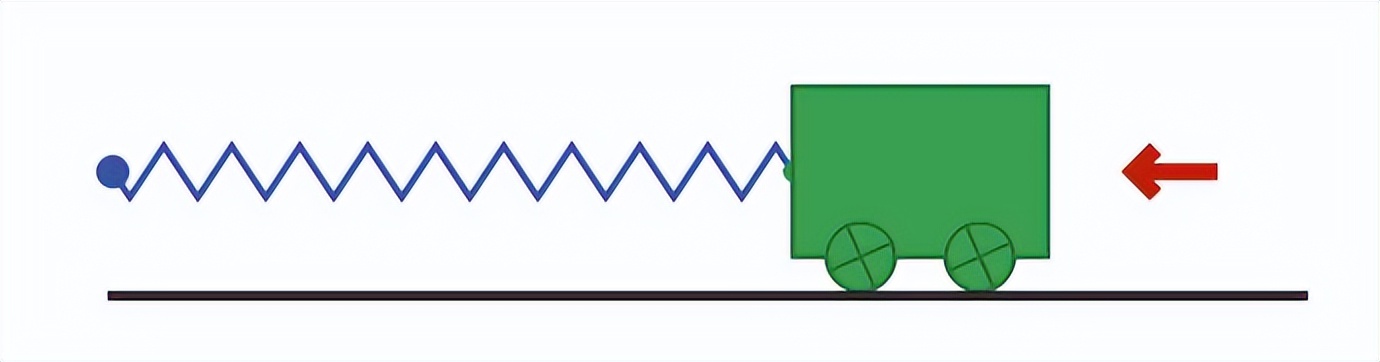
弹簧的力使手推车加速。当手推车到达中点时，弹簧不再处于张力状态，所以它不再拉手推车。然而，手推车现在获得了动量。它继续移动，压缩弹簧，减慢手推车的速度。最终，手推车停下来，但现在弹簧被压缩，导致手推车开始朝相反方向加速。这个运动是循环的，如下所示：

如果我们假设一个完美的系统，手推车将永远持续这种运动。

手推车完成一个周期需要多长时间

系统的所有重要变量都是1。手推车的重量是1千克，弹簧的力是1牛顿每米，弹簧最初伸展的长度是1米。

那么手推车完成一个周期需要多长时间呢？你可能会猜测它需要1秒。或者也许每个方向1秒，所以总共2秒。你可能不会猜测这个时间取决于一些你在学校几何课上学到的奇怪的无理数。

手推车的运动方程

现在让我们推导描述手推车运动的方程。

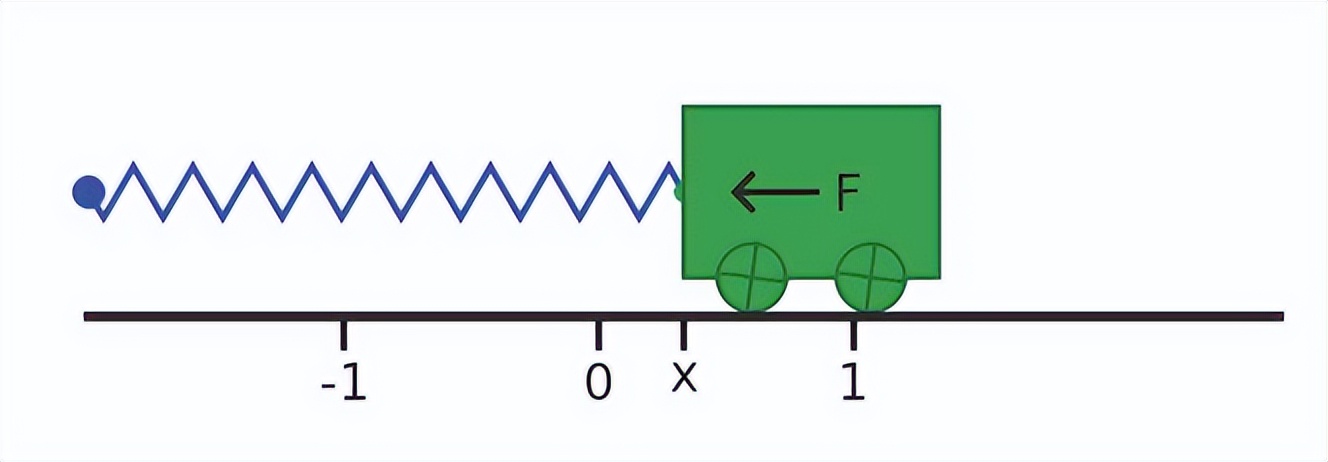
轨道上标有点0，是手推车的静止点；以及点1，是释放手推车之前的起始点。图中显示了手推车在x位置，还显示了弹簧施加的力F。

被拉伸的弹簧所施加的力由胡克定律给出：

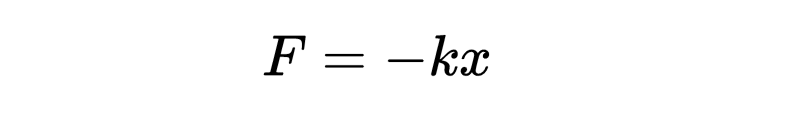
这意味着弹簧所施加的力F等于伸展长度x乘以弹簧常数k的负数。引入负号是因为力总是与伸展方向相反。

弹簧常数k是衡量弹簧刚度的一个度量，在这个例子中k = 1。所以力是：

那么手推车在这种力的作用下是如何移动的呢？根据牛顿第二定律，力使物体加速，力等于质量乘以加速度：

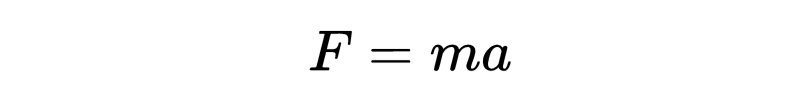
由于手推车的质量是1千克，所以这个方程简化为：

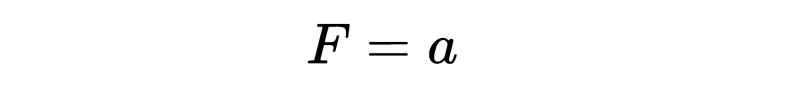
我们可以用x表示加速度。我们知道速度是x变化的速率，加速度是速度变化的速率。这意味着加速度是x变化速率的变化速率。这可以写成x的二阶导数（x的两次微分）：

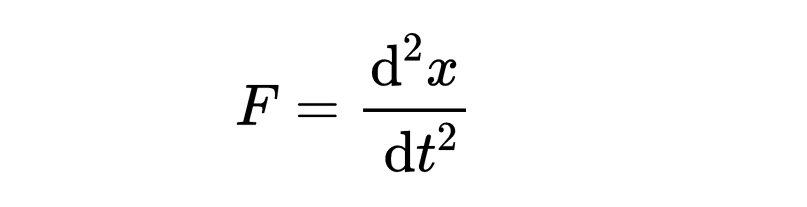
现在有了两个关于F的表达式，我们可以将它们等同起来，给出一个描述x随时间变化的方程：

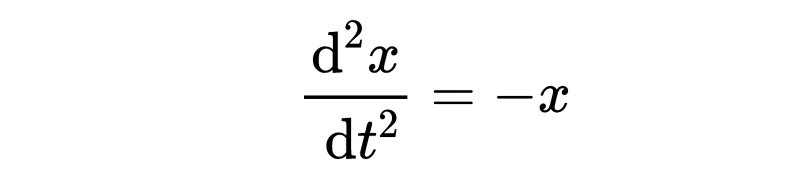
这种类型的方程称为微分方程。这个方程告诉我们x作为时间t的函数变化：

它还告诉我们这个函数有一个特殊的性质，即如果对函数进行两次微分，结果等于原函数的负数：

结合初始条件（例如，当t为0时的位置和速度），我们可以求解方程。

解方程

有多种方法可以解这个方程。我们将使用麦克劳林级数来解它。对于这个求解方法，我们假设方程以无限多项式的形式表示：

麦克劳林方法允许我们数值上评估这个表达式，以找到一个近似解。方法如下：

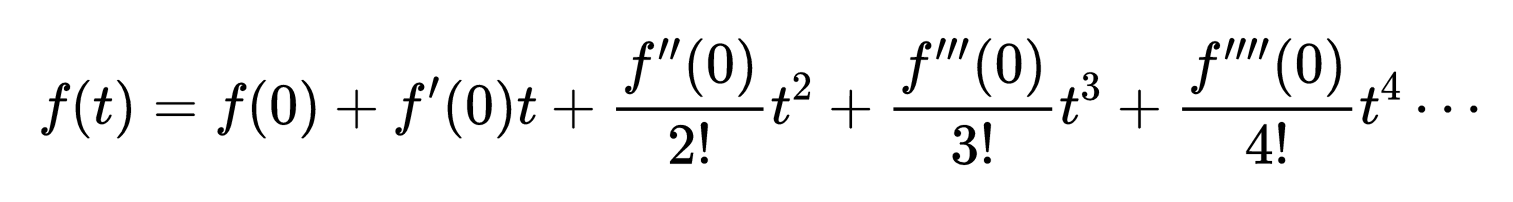
这是什么意思？它告诉我们手推车的运动被描述为时间的多项式函数，其中每个系数可以通过对某个函数f在时间t=0这一特定点的评估来确定。具体来说，这通常涉及到计算函数f在t=0时的值、导数、二阶导数、三阶导数等等。

计算a0

第一项，a0，等于f(0)，即当t为0时f的值。但我们不知道函数f是什么，这正是整个问题所在。那么我们如何计算它在0处的值呢？

幸运的是，我们不需要知道任何关于函数f的信息就可以计算它在时间0处的值。f=x，我们知道x的初始值（当t = 0时）是1，因为这是我们放开手推车之前的起始位置。所以a0=1。

计算a1

第二项，a1等于f’(0)。即函数f的一阶导数，在0处评估。但既然我们不知道函数是什么，我们如何对它进行微分呢？

同样，我们不需要知道任何关于f的信息就可以在t = 0时计算它的导数。f的一阶导数代表手推车的速度。我们知道在时间0时手推车是静止的，所以速度是0。所以a1=0。

计算其他项

显然，要完全解方程，我们需要找到f’’(0)，f’’’(0)等。我们可以求出f’’(0)，因为原始微分方程是：

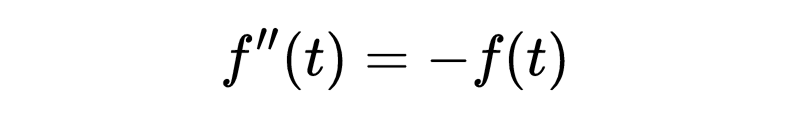
因此可以推断出：

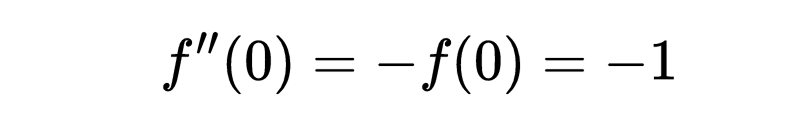
我们可以通过对二阶导数微分来求出第三阶导数f’’’(t)：

再次使用了f’’(t)=-f(t)的事实。在0处评估得出：

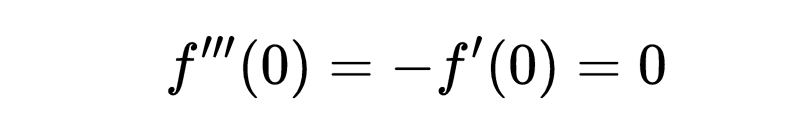
我们可以通过对二阶导数两次微分来求出第四阶导数f’’’’(t)：

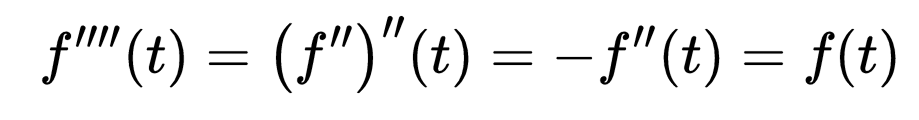
这次两次使用了f’’(t)等于-f(t)的事实。在0处评估得出：

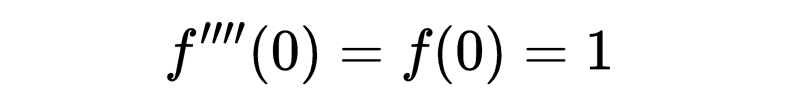
f(x)的最终公式

f(0), f’(0), f’’(0)等的值形成一个重复循环 1, 0, -1, 0, 1, 0, -1, 0…

我们可以将这些值代入麦克劳林公式得出：

去掉0项，并整理得出：

这是描述手推车运动的方程。

绘制手推车的运动

手推车的实际行为是怎样的？我们可以通过绘制上述方程的图形来发现。

这是计算到包括t的8次方项的函数：

请注意这是一个有限的级数，它不包含超过t的8次方的项。这是这个函数的图形：

在这个图形中，x轴代表时间，y轴代表手推车的位置。

图形一开始看起来相当合理。手推车从x = 1开始，当接近中点x = 0时加速，然后当弹簧压缩时再次减速，向着x = -1移动，然后减速到速度为0，然后改变方向。如果我们在现实生活中做这个实验，我们会看到它从+1到-1需要稍微超过3秒，正如图形预测的。

然而，图形然后飞速升至无穷。这当然是不正确的。问题在于我们在近似中只保留了5项，当t大于大约4时，缺失的项变得重要，因此忽略它们会得到一个糟糕的结果。

现在让我们再试一次，包括直到t的18次方的项：

这个更好：

图形显示手推车从1到-1再回到1，相当准确。但大约8秒后，情况开始变得糟糕。这是出于之前相同的原因，即没有足够的项来准确地模拟较大t值的函数。

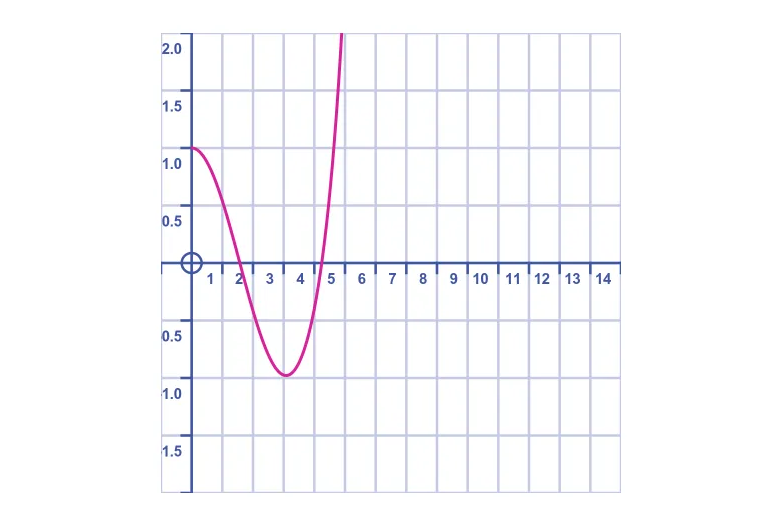
最后，我们将尝试使用直到t的38次方的项：

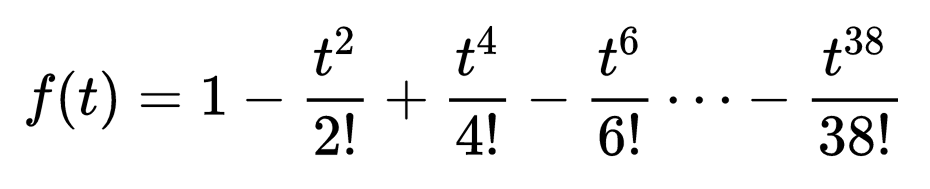
正如我们预期的那样，手推车来回弹跳。在一个没有摩擦或其他损失的理想系统中，它将永远持续：

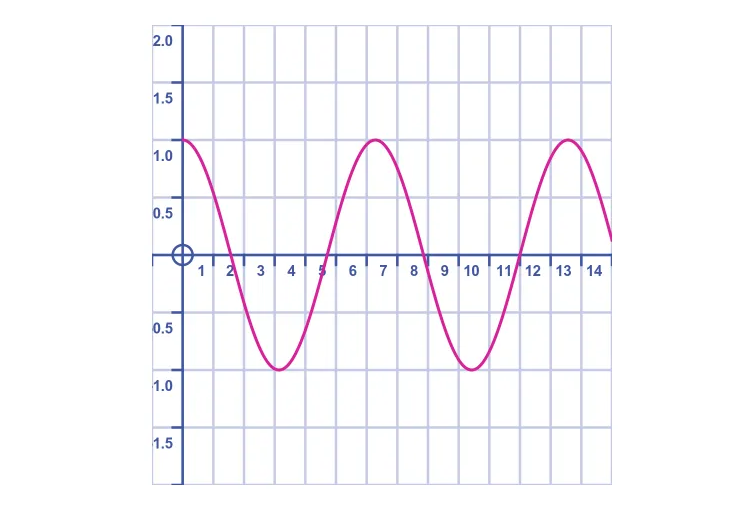
即使方程中有所有额外的项，它最终也会像其他情况一样偏离轨道。但是运动是循环的，所以如果我们能准确地模拟第一个循环，我们就可以简单地重复其他的循环。

手推车完成一个周期需要多长时间？

回到最初的问题，手推车完成一个周期需要多长时间？

当手推车的位置回到1时，它完成了第一个周期。在这张图中，它位于红色圆圈所指示的峰值处：

从视觉上可以看到，这发生在6秒多一点的时间后。我们可以通过计算上面的公式的几个不同值并找出最接近1的值来获得更好的近似值。

一系列尝试得出，这个值在6.2830和6.2835之间的某个地方。下面这个表计算函数在这两个极限之间的各种值

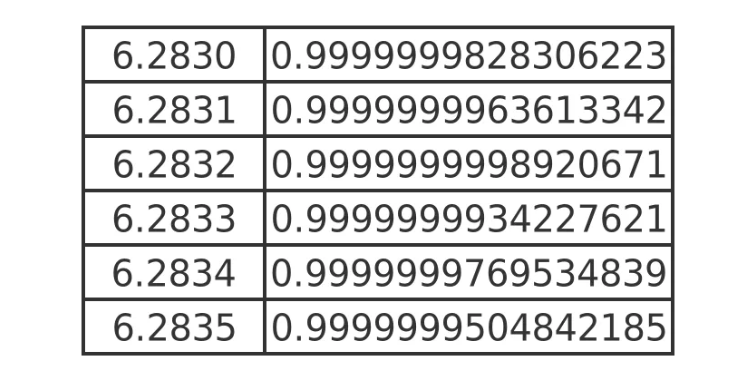
这告诉我们，最接近手推车周期的近似值是6.2832。考虑到所有系统参数都等于1，这似乎是一个相当奇怪的数字。

你可能知道2π大约等于6.283185307。我们得到的值非常接近π。

如果使用更多项（例如使用直到t的100次方的项）来进行更好的近似，会发现结果更接近2π。事实上，如果在方程中使用足够多的项，我们可以得到任意接近2π的结果。基于此，我们可以说确切的周期是2π。

你可能还注意到这个函数看起来像余弦函数。这是因为我们一直在使用的麦克劳林级数是余弦函数的级数。余弦函数的周期是2π，这进一步验证了之前的结果。

π并不是完全关于圆的。它实际上还与一个简单微分方程的解有关：

那么为什么π会出现在圆的公式中呢？这是巧合吗？当涉及到无理数时，没有所谓的巧合。圆的周长和面积受与我们上面使用的相同微分方程的控制，因此解涉及π。只是在这种背景下，π被发现的时间远远早于微分方程。