解析数论是数论的一个分支，它使用数学分析的方法研究整数的性质。这个领域起源于18世纪和19世纪，当时数学家们开始使用微积分和复分析中的工具来解决数论中的问题。解析数论的主要特点是它利用了连续函数、级数、积分等分析学的概念和方法，以研究本质上是离散的数论问题。

1859年，黎曼在他的一篇论文，即关于一个给定大小下的素数的数量（On the Number of Prime Numbers less than a Given Quantity）中考察了欧拉函数，

但有一点关键性的区别，即他考虑了复的s值。准确地说，定义了我们今天所说的黎曼ζ函数：

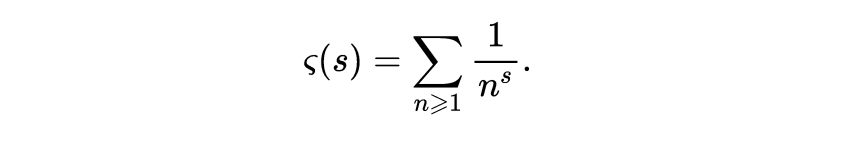
很容易证明，这个级数当s的实部大于1时收敛，而这一点我们已经对于实的s看到了。然而，允许s取复值的一个重大好处是，这样得到的是一个全纯函数，而我们可以利用解析延拓（Analytic continuation）的过程使得ζ(s)对所有的复数s≠1都有意义。

全纯函数是复分析中的一个核心概念，它指的是在复平面上定义的、处处可微的复变函数。全纯函数也被称为解析函数（analytic function）。这些函数的主要特点是它们在其定义域内不仅连续，而且可以无限次微分。

解析延拓是数学中的一个重要概念，特别是在复分析领域。它是指将一个在某个区域内定义的解析函数（全纯函数）扩展到更大的区域，同时保持函数的解析性（即可微性和局部由其泰勒级数表示的性质）的过程。

简单来说，解析延拓就是在不改变原有函数定义的情况下，将其定义域拓展到更广的区域。

黎曼证明了一个很值得注意的事实，这件事实确定了高斯关于直到x为止的素数的数目的猜测等价于对黎曼ζ函数ς(s)的零点（即使得ζ(s)=0的s之值）深刻理解。

黎曼的深刻的工作催生了这个学科分支，因此值得把这个联系了两个表面上不相干的主题的论证，至少是把它的关键之点，在这里说一个大概。

黎曼从欧拉公式开始。不难证明这个公式对于复的s也是有效的，只要s的实部大于1即可。所以有

取两边的对数再作微分，就得到

我们需要有一个办法把适合p≤x的的素数与适合p>x的素数区别开来，就是说，我们要计数的只是适合x/p≥1的素数p，而不需要适合x/p<1的那些素数p。只要使用阶梯函数就可以做到这一点，

在y=1处，令这个函数取平均值1/2是方便的。Perron公式是一个在解析数论中的一个强大的工具，把这个函数表示为一个积分如下：

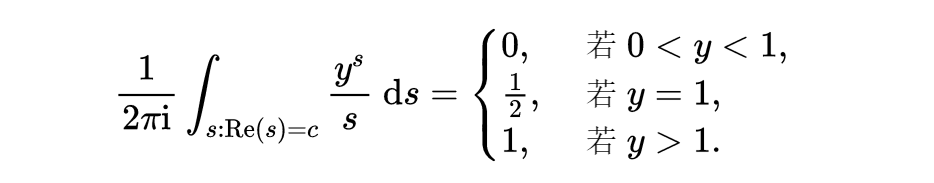
这个积分是在复平面的一条铅直直线上的道路积分，这条直线上的点就是所有的c+it，t∈R。把Perron公式用于y=x/p^m，这样就只保留了相应于p^m<x的项，而抛弃了相应于p^m>x的项。为了避免因子“1/2”，假设x不是一个素数的幂，[从而不可能有p^m =x]。这样就得到了

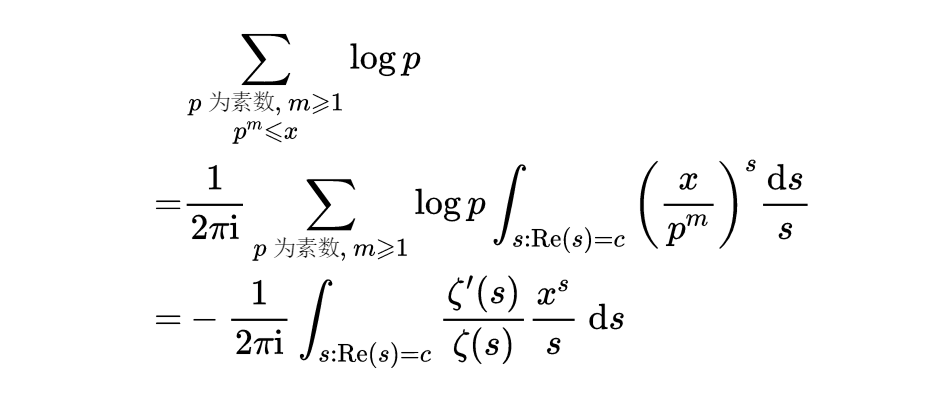
式（1）

如果c充分大，则可以论证在上式中交换积分和求和的顺序是合法的，因为这时出现的积分和级数都是绝对收敛的。上式左方并不是直到x为止的素数的个数，而对于每一个素数p都赋予了一个权重log p。然而，只要能够证明当x很大时，x是这个加权计数的好的估计，就可以得出高斯的预测。注意，上式中的和是小于和等于x的整数的最小公倍数的对数，这或许可以解释为什么素数个数的加权计数函数是一个自然要考虑的函数。另一个解释是，如果p附近的素数的密度是1/log p，则在乘上权重log p以后，素数的密度就变成处处为1了，

用一点复分析知识就会知道，利用柯西的留数定理（（Cauchy's Residue Theorem）），就可以用被积函数：

的“留数”来估计(1)式右方的积分。

柯西的留数定理是复分析中的一个重要结果，它提供了计算围绕奇点的闭合路径上复函数积分的强大工具。这个定理是解析函数理论中的核心部分，尤其是在计算复平面上的围道积分时。

进一步还会知道，对于每一个除（有限多个极点外）处处解析的函数f(s)，f'(s)/f(s)的极点就是f(s)的极点和零点。f’(s)/f(s)的极点阶数均为1，而留数就是相应零点的阶数或者相应极点的阶数反号。利用这些事实，就可以得到显式公式

式（2）

这里ζ(s)的零点都要按重数计数，就是说，如果p是ζ(s)的一个k阶零点，则在(2)式右方的和式中就会出现k个p。有这样一个公式把直到x为止的素数的个数用一个含有很复杂的函数的零点的准确的公式表示出来，这是很惊人的事，这样就可以看到为什么黎曼的工作拉动了人们的想象力，而且有那么大的影响。

黎曼作了另一个惊人观察，使我们很容易在复平面的左半平面（函数ζ(s)本来在那里并没有自然的定义）决定ζ(s)的值。他的思想是：用一个简单的函数来乘ζ(s)，使得其乘积ξ(s)满足一个函数方程式：

只要取

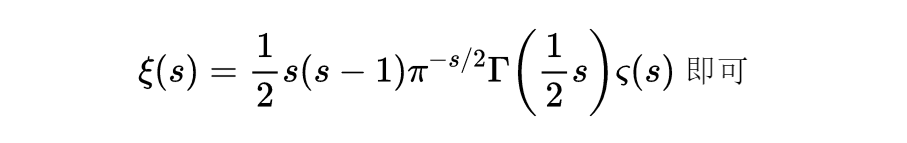
式（3）

这里的

就是著名的Camm函数，它在正整数点上就是阶乘函数，而对所有其他的s都是连续的。

仔细地分析欧拉函数就会得出，ζ(s)在Re(s)>1时没有零点；再用(3)式又可以导出，在Re(s)<0时，ζ(s)的仅有的零点只是负偶数（称为ς(s)的“平凡零点”），所以，为了利用(2)式，只需要在临界带形，即适合0≤Re(s)≤1的s的集合中决定ς(s)的零点就行了。黎曼在这里又给出了一个非凡的观察，而如果它是真的，就会给予我们对几乎所有有关素数分布的问题以巨大的洞察力。

黎曼假设如果0≤Re(s)≤1，而且ζ（s）=0，则Re(s)=1/2。

已经知道，在直线Re(s)=1/2上有无限多个s(s)的零点，而且当沿此直线上行时零点越来越密集。已经用计算来验证黎曼ζ函数的前几十亿个最低的（就是Im(s)最小的）零点，而结果都是与黎曼假设相符的，可以证明ς(s)的零点中至少有40%是符合黎曼假设的，同时有许多不同的关于素数分布及其推论的有启发性的断言，也都与黎曼假设符合得很好。尽管如此，黎曼假设仍然是一个未证明的假设，也是整个数学里最著名也最诱人的假设。

黎曼是怎样想出他的“假设”的呢？黎曼的论文完全没有暗示，他是怎样碰上这个非凡的假设的。后来很长的时间里，这个假设就成了人类单纯凭着纯粹的思维就能达到何等的高度的一个例子。然而到了1920年代，西格尔和韦伊得到了黎曼的未发表的手稿，从那里就可以看得很清楚，黎曼硬是用手工计算了ζ(s)的最低（即虚部绝对值最小）的一些零点到小数几十位——这就是“单纯凭着纯粹的思维”！尽管如此，黎曼假设仍然是想象力的巨大飞跃，而同时还找到计算ζ(s)的零点的算法更是一个了不起的成就。

如果黎曼假设为真，不难证明下面的估计：

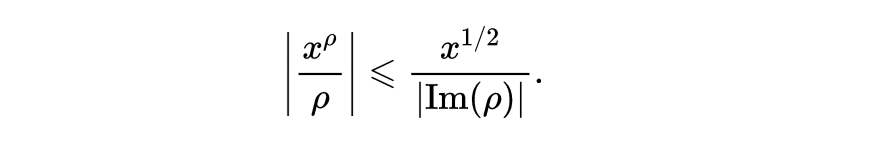
把这个式子代入(7)，可以导出

式（4）

这个式子又可以进一步“翻译”为，

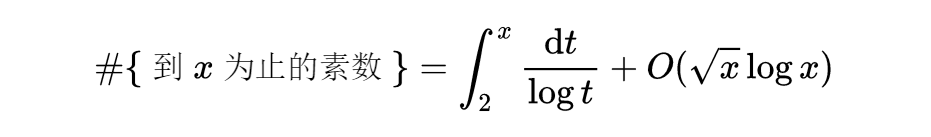
式（5）

事实上，这些估计当且仅当黎曼假设为真时成立。

黎曼假设不是一个容易懂、容易完全理解的东西。与它等价的(5)式可能要容易一些。另一个版本也是我比较喜欢的一个版本是：对于每一个N≥100，

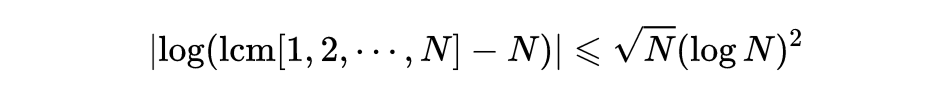
现在集中考察高斯关于直到x为止的素数的个数的猜测的超出的量，可以用下面的近似，它当且仅当黎曼假设为真时可以从(2)式导出：

式（6）

此式左方就是高斯关于直到x为止的素数的个数的猜测的超出的量除以某个增长性与√x相近的函数。如果看一下下表，

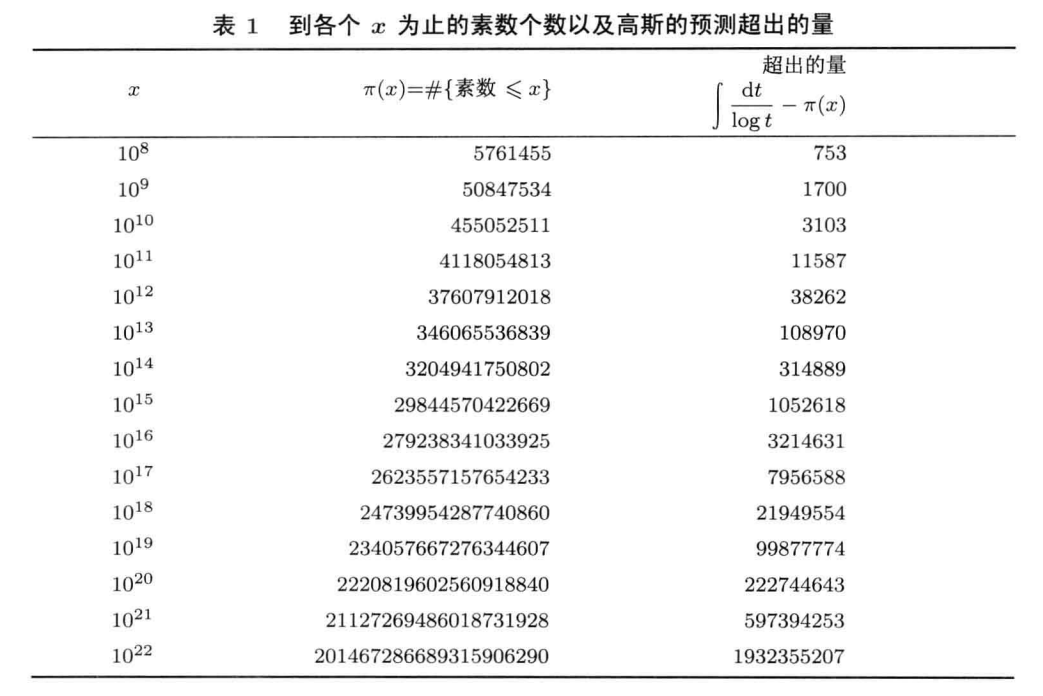
这个分式似乎就应该近于一个常数。但是，如果再看一下此式右方，这一点似乎又不太对。右方的第一项“1”，相应于(2)式中素数的平方的贡献，其余各项相应于(2)中涉及ζ(s)的零点的各项。这些项都有一个分母γ，所以这些项中最重要的是相应于最小的γ的项。此外，这些项都是正弦波，所以它们是震荡的，有一半时间为正，另一半时间为负。其中出现的“log x”表示这些震荡来得很慢（这就是为什么在表中很难看到这些震荡），但是震荡确实是发生了的，而且(6)中的量最终会变成负的。迄今谁也没有找到过使它为负的x，而最好的猜测是：这个情况将在

时发生。但是表1中的x最大也只到达10^22，我们又怎么会猜到x接近于10^316时的事情呢?我们从用(6)式右方的前1000项来逼近左方开始。只要感到右方还有可能为负，就多用一些项，例如用100万项做下去，直到相当肯定结果可能为负时结束。

为了更好地理解一个给定的函数，把它表示成像这样的正弦和余弦的和并不是少见的。事实上，研究音乐中的谐音时，人们就是这样做的，从这个观点看来，(6)这样的式子是不可抗拒的。有些专家声称：“素数中自有乐音在”，这样就使得黎曼假设不仅是可信的而且是很合人心意的。

要想不附加条件地证明所谓素数定理

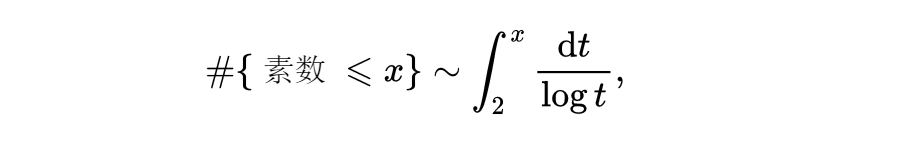
也可以采取和上面同样的途径。因为我们并不想得到关于直到x为止的素数的个数的很强的近似，所以只需要证明直线Re(s)=1附近的零点个数对于(2)式的贡献不大即可。到19世纪末，这个工作归结为证明在直线Re(s)=1上实际上没有零点存在，最后是瓦菜·布散和阿达玛在1896年完成了这件事。

其后的研究给出了临界带形0≤Re(s)≤1的越来越宽的子区域，在其中也没有ζ(s)的零点（这样也就改进了关于直到x为止的素数的个数的近似），但是怎么也没有接近于证明黎曼假设，而使得黎曼假设仍旧是整个数学中十分突出的未解决的问题。

像“直到x为止的素数有多少？”这样形式简洁的问题，当然值得有一个形式简洁的回答，值得有一个只使用初等方法而不是用上复分析中的全武行的解答。

然而，(2)式告诉我们，素数定理当且仅当在直线Re(s)=1上没有ζ(s)的零点时成立，这样就使人们以为复分析会出现在其证明中是不可避免的事情。

1949年，Atle Selberg和Paul Erdös给出了素数定理的初等证明而震惊了整个数学界。这里“初等”并不意味着“容易”，只是说这个证明并没有用复分析这样的高深工具——事实上，他们的证明是很复杂的。他们的证明必定是以某种方式证明了直线Re(s)=1上没有ζ(s)的零点，而且，他们所用的组合方法狡黠地把一个微妙的复分析证明掩盖起来了。