有一个数学谜题非常违反直觉，即使你知道答案，你也会觉得很不可思议。这篇文章，我将深入挖掘这个数学谜题并完全解释它。

假设有100名囚犯，编号为1到100。

在100个纸条上写着他们每个人的号码，即1-100，

把这些号码随机放在一个房间的100个盒子里，盒子也从1-100编号。每个囚犯一个接一个地进入房间，打开100个盒子中的任意50个，寻找他们的号码。之后，他们必须离开房间，离开房间后，不能以任何方式与其他囚犯沟通。

如果所有100名囚犯都能找到自己的号码，他们都将被释放。但如果有人没有找到他的号码（即使只有一个没找到），他们都将被处决。

囚犯们可以在他们进入房间前制定策略。那么他们最好的策略是什么？

如果他们每个人随机寻找自己的号码，那么每个囚犯找到自己号码的概率是50%。因此，100名囚犯都找到他们的号码的概率是

这个结果等于，

但如果我告诉你，用正确的策略，可以将他们的生存机会提高到近三分之一，也就是提高了近30个数量级。你一定会感到惊讶。我来告诉你这个策略。

这个方法（策略）涉及数学的一个令人难以置信的特征。如果你想不到也很正常，毕竟提出这个谜题的人——计算机科学家彼得·布罗·米尔特森，也没有独立想到。后来，（在别人指点下）米尔特森在一篇论文中公布了答案。

下面是囚犯们的逃生策略：

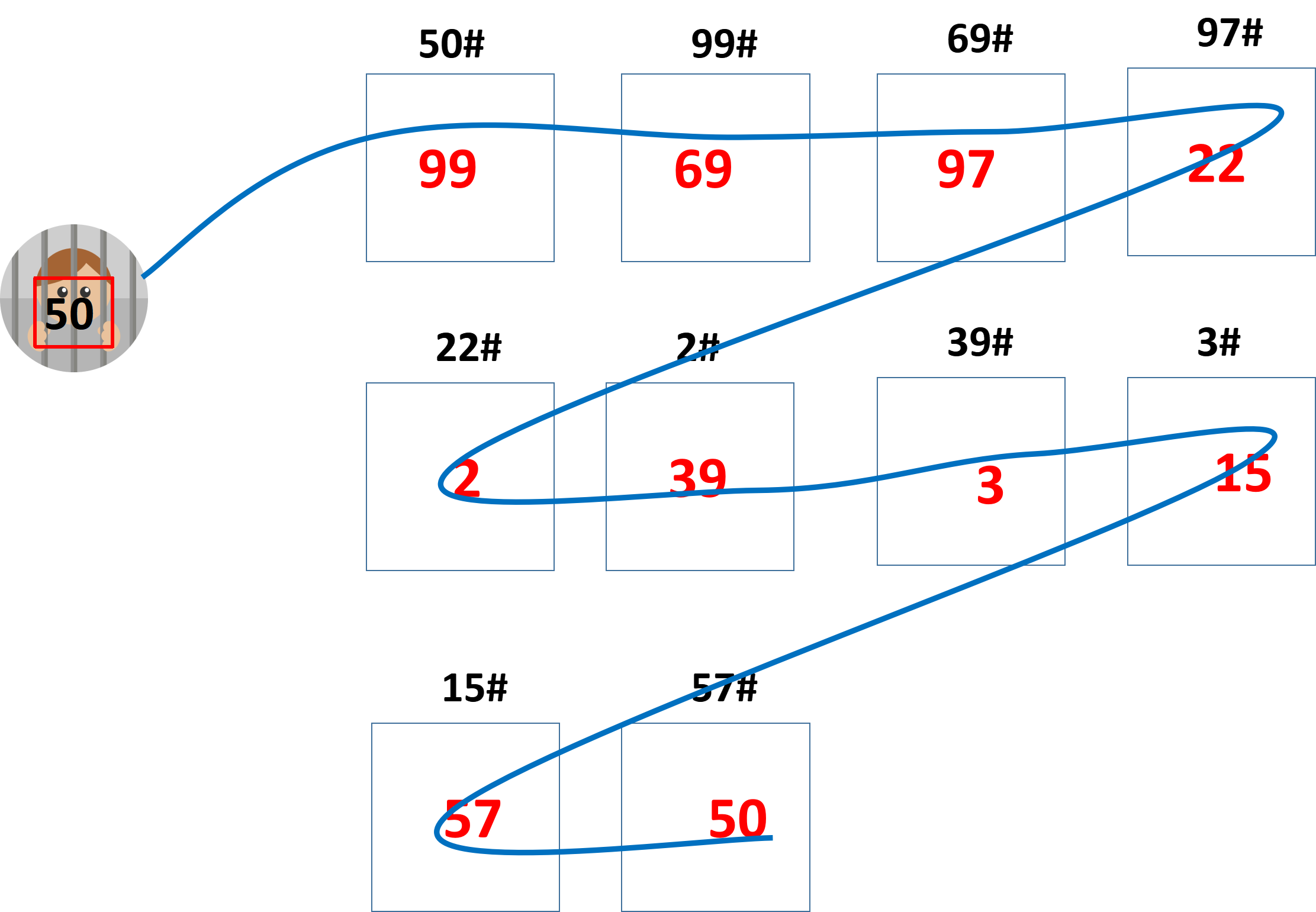
假设你是其中一名囚犯（假设编号是50），当你进入房间时，打开编号是你号码的盒子（即50号盒子），里面的纸条上的号码可能不是你的（假设是99），但这没关系，转到99号盒子，看看里面的号码（69），然后转到69号盒子，依此类推。一直这样做，直到找到带有你号码的纸条。

如果你找到了你的号码，那么，根据盒子里的内容（50），你要回到开始时的盒子（50号），这样就形成了一个循环。

这个简单的策略使得所有囚犯找到他们的号码的概率超过30%。但是这里的数学原理是什么？

首先要注意的是所有的盒子都会成为一个封闭的循环。最简单的循环是，一个盒子的编号与这个盒子里纸条的号码是一样的，比如50号盒子里纸条上的号码是50。

如果你是1号囚犯，那么你就去1号盒子，它里面有1号纸条，那你就成功了。你的号码是一个长度为1的循环；

但也可能是一个长度为2的循环，比如说1号盒子指向7号盒子，而7号盒子又指回1号盒子。

或者可能是一个长度为3的循环，或者4，或者5，或者任意长度，一直到100。最长的循环会将所有数字连接成一个单一的循环。但更一般地说，任意随机排列这些盒子里的纸条将产生一些较短和较长循环的混合。

当你从一个贴有你号码的盒子开始时，你一定会在一个循环上。

所以决定你能否找到你的号码的关键是循环的长度。如果你的号码在一个长度小于50的循环上，那么你肯定会找到你的号码。但是，如果你的号码是一个长度为51或更长的循环的一部分，那么，你搜索50个盒子，是找不到你的号码的。

当你打开贴有你号码的盒子时，你实际上是从离你号码最远的循环点开始的。你想知道指向这个盒子的纸条在哪里，你必须沿着数字循环，一直走到尽头。

这意味着，如果囚犯们遵循这个策略，并且最长的循环是51，那么不仅仅是一两个囚犯无法找到他们的号码，而是这个循环上的所有51个人都无法找到。

所以，所有囚犯成功的概率，是随机排列的一百个数字不包含长度超过50的循环的概率。这个概率为三分之一左右，但是我们如何计算呢？

想象一下把所有不同的情况写下来，可以是100个盒子以形成一个长度为100的循环，这样的情况是：盒子1指向盒子2，盒子2指向盒子3，盒子3指向盒子4，依此类推，一直到100，然后盒子100会指回盒子1；

或者可以是随机的，盒子5指向盒子99再指向盒子17等等，最后一个是63，盒子63指回盒子5。

那么这一百个盒子的不同排列组合有多少种？

对于第一个盒子，有100个不同的盒子可以选择（指向）；第二个盒子，因为已经用了一个，所以只能从99个盒子中挑选；接下来的一个，可以从98个盒子中挑选，依此类推，直到最后一个盒子。

所以不同排列组合的总数将是100乘以99，乘以98，乘以97，一直乘到1。这是100的阶乘。有100阶乘种不同的方法创建一个长度为100的盒子循环。

但是我们不能忘记这些不是数字线，而是循环。所以下面这些看起来不同的情况，实际上是相同的循环。

所以长度为100的循环的总数是100阶乘除以100。

那么任何随机排列的100个盒子，包含长度为100的循环的概率是多少？显然，答案是1/100。这是一个普遍的结果，长度为99的循环的概率是1/99。长度为98的循环的概率是1/98。因此，长度超过50的循环的概率是，

囚犯有69%的失败概率，这意味着成功的概率为31%。难以置信吧！使用循环策略，100个囚犯找到他们的号码的可能性，比仅仅是两个囚犯随机选择的概率还要大。

那么使用循环策略，每个囚犯单独找到他们的号码的概率是多少？每个囚犯仍然只能打开一半的盒子，所以他们个人的机会仍然是1/2，但这些概率，不再彼此独立。

想象一下，这个实验重复了一千次。如果每个人都是随机猜测，你会期望在大多数情况下约有50个囚犯会找到他们的号码。但使用循环策略，所有囚犯有31%的概率会找到他们的号码。而69%的概率，少于50人找到他们的号码。囚犯们要么一起赢，要么大多数人一起输。

但是，如果有一个恶意的狱警，知道了囚犯们的这个循环策略怎么办？那么，他们可以把数字放在盒子里，以确保它们形成一个长度超过50的循环。在这种情况下，囚犯们注定要失败吗？

令人惊讶的是，答案是否定的。他们可以通过重新编号盒子来反击。例如，他们可以给每个盒子的编号加上5。循环是由纸条的位置和盒子编号共同决定的。重新编号盒子基本上等同于重新分配纸条。因此，问题又回到了随机循环的排列组合上，这意味着囚犯们仍然有31%的生存机会。

现在，如果增加囚犯的数量会发生什么呢？

当有1000名囚犯，每人允许打开500个盒子时，你可能会认为他们成功的机会会大幅下降，但是通过计算，结果是30.74%，

比100名囚犯只低了半个百分点。对于100万名囚犯，成功的概率是30.685%，

这比10亿人的概率只高一点。所以，成功的概率的确会接近一个极限。那么这个极限是什么呢？

我们一直在使用的公式是1减去失败的概率，即

我们可以将这个级数表示为矩形的面积和，

并且有一条曲线，

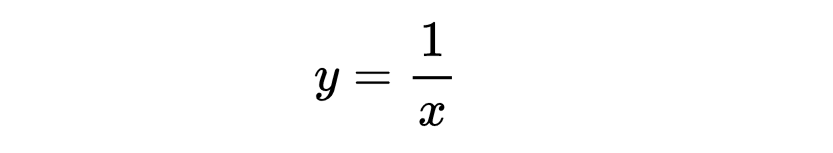
所以要求得失败的概率，我们只需取1/X的积分，从n到2n，

这个积分的结果是ln2。那么成功的概率就是1-ln2，约为30.7%。无论有多少囚犯，使用这种策略，成功的概率都超过30%，

循环策略的美妙之处在于将每个人的结果联系在一起，而不是让每个囚犯走进去各自为战。