之前的一篇文章“证明黎曼猜想的新几何，把数学之美展现得淋漓尽致，成就数学之梦”提到，黎曼ζ函数是L函数的最简单示例：

那么，L函数是什么呢？数学的核心中有一个非常深刻的主题，叫做对偶性（duality）。在线性代数中，有向量和它们的对偶对象，叫做泛函（functional）。在量子力学中，有bra和ket。在群论中，有共轭类（conjugacye）和不可约表示（irreducible representation）。在数论中，有素数和L函数。

下面是一个非常非形式化的解释：L函数是与素数对偶的对象。我们将会得到一个更精确的关于L函数的定义，看两个简单的例子。

L函数的两个例子

黎曼ζ函数可以被写为：

这里，分子都是1。一般的L函数可以被写为：

其中这些分子是一些数的序列：

这些数在这个序列中被称为L函数的狄利克雷系数（Dirichlet coefficients）。

这是一个L函数的例子：

1,1,0,1,2,0,0,1,1,2,0,0,2,0,0,1,2,1,0,2,0,0,0,0,3,2,0,...

这是非常非常特殊，几乎是神奇的序列之一，恰好是一个L函数或者是一个L函数的系数。你能看出这个序列中的规律吗？能预测出下一个数字或者接下来的10个数字吗？

下面是一个更复杂的L函数的例子：

1,-1,-2,1,0,2,1,-1,1,0,0,-2,-4,-1,0,1,6,-1,2,0,-2,0,0,2,-5,4,…

这里的规律是什么？

上面两个序列是Motivic L函数的例子，这是从多项式方程构造的L函数。第一个例子是从方程x平方加1等于0构造的L函数。我们用字母K标记这个方程。

第二个例子是从以下方程构造的L函数，我们用字母E标记这个方程。

当我说“从……构造”，是指一种机器，它以一个方程作为输入，生成一个序列作为输出。

如果你想先把这个机器当作一个黑盒子来对待，可以借助Sage软件。对于第一个方程，只需要键入这一行代码：

这里的变量是x。这个特定的方程定义了所谓的数域（NumberField），我们要求这个数域的前20个L函数系数。

对于第二个方程，你可以输入这个代码：

在这里我们看不到实际的方程，而是简写成"14. a5"。这个方程定义了一个叫做椭圆曲线（elliptic curve）的东西，然后求前20个系数。

这篇文章的主要目标是研究这两个L函数，解释这些序列如何从方程中出现，找到其中的基础模式（规律）。这些模式将是数学家所称的朗兰兹计划（langlands program）的实例。

LMFDB

在我们深入这两个序列的具体情况之前，我想先给你们看一下LMFDB，即L函数和模型形式数据库（L-functions and modular forms database）。

在LMFDB中，你会找到L函数以及产生L函数的对象。

你可以看到椭圆曲线，数域。在名人堂里，有黎曼zeta函数，拉马努金delta函数等等。现在，点击网页左上角的“Universe” ，你会看到：

在这里，我们看到了这个著名的图片，展示了朗兰兹计划中不同数学世界之间的联系。最上面是L函数。L函数可以被视为独立的实体，但我们通常认为L函数是由某个其他对象构造的。而这些其他对象，我喜欢称之为原始对象。在这张图片中，我们可以看到三大类的原始对象。Motivic world在右边，Automorphic world在左边，伽罗瓦表示在下面。所以每个原始对象都会产生自己的L函数。

在数学中，Motive是一种抽象对象，用于统一和理解代数几何中各种不同的同态类。它们被认为是数学中的粒子”，是一种用于研究和理解更复杂数学结构的工具。Motive的概念来自于亚历山大·格罗滕迪克（Alexander Grothendieck）在1960年代的一些想法，这些想法目标是为了解决一些基础问题，包括一些来自数论和代数几何的问题

现在，已经有两个Motive了，因为任何多项式方程都可以被视为一个Motive。所以K是一个Motive，E也是一个Motive。

Motivic K有它的L函数“L下标K” ，

对于E也是类似的，

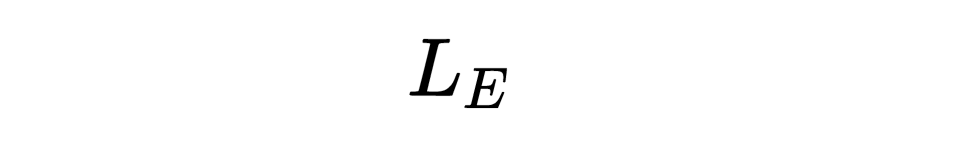
这就是我们刚刚看到的那两个数字序列。现在，被称为“朗兰兹互换（langlands reciprocity）”的猜想说，当有一个Motivic L函数，也就是从右边（Motivic world）过来的L函数，可以从左边（Automorphic world）找到一个Automorphic对象，能给出同样的L函数。

如果有一个Motivic L函数，并且你成功地证明了一个对应的Automorphic对象存在，那么L函数就具有所谓的解析延拓和函数方程。这反过来意味着，可以讨论特定的L函数的黎曼假设。到目前为止有以下的主要观点：

这里存在着质数和L函数之间的对偶性，可以这样理解：每个L函数可以被视为某个希尔伯特空间中的一个向量。然后，每个质数可以被视为对偶希尔伯特空间中的一个向量。

存在一种机器，它以多项式方程作为输入，产生L函数作为输出。

回到这两个例子，K和E，以及它们的L函数。

K的神秘性

让我们看一下第一个L函数。这个L函数的序列是：

1,1,0,1,2,0,0,1，……

让我们把这些数字放入一个表格，

第一个2是在a_5这里。在a_25这里有一个3。初始的项是1,1,0,1,2。我想给出一个如何从等式x^2+1=0构造这个序列的简化解释。我们知道，x^2+1=0用于从实数过渡到复数。我们要做的是从实数开始，引入一个新的数字，称之为i，其性质是i^2+1=0。使用加法和乘法这两个运算，可以生成更多的数字，所有这些数字加在一起，称之为R与i的并集，或者用一个特殊的符号C表示，就是复数。

现在，我们可以再做一次同样的事情，但这次从整数开始，而不是实数。所以，像以前一样引入新的数字i，考虑所有可以通过乘法和加法产生的数字。这些数字的集合被写作Z与i的并集，

没有特殊的符号表示它们，它们被称为高斯整数（Gaussian integers）。复数可以被视为一个二维平面。然后高斯整数就是具有整数系数的点的子集。例如3+2i或2-i，所以所有网格的交点都是高斯整数。

定义：一个高斯整数a加bi的范数（Norm）就是a平方加b平方。例如，3+2i的范数是

现在让我们计算几个小的高斯整数的范数。0的范数是0，1的范数是1，i的范数也是1。1+i的范数是2，2的范数是4，2+i的范数是5。就这样继续下去。

现在让我们数一数，有多少点的范数是1，总共有四个点，

但是有一个规则，那就是当一个点可以通过90度旋转变成另一个点时，他们就被认为是同一个点。所以这四个点，它们只算作一个，这个规则来自于乘以i等同于旋转90度的事实。

所以，范数为1的点有一个。范数为2的也只有一个点。范数为3的点则没有。范数为4的点在图片上有两个，但它们被算作同一个。范数为5的点有两个。范数为6和7的点都没有，现在你可能已经认出了这个序列：1101200。

让我们看下25，它有三个点，

这在一定程度上解释了方程x^2+1=0如何产生序列1101200……，这就是K的L函数。

所以我们已经从方程过渡到了L函数。现在有两个主要的挑战。

首先，还不容易看出如何在不实际计算高斯整数的情况下计算序列的下一项或接下来的10项。有没有递归或某种规则可以根据前面的项生成下一个项呢？

第二，我们以某种方式从方程x^2+1=0得到了L函数。有没有一种方法可以直接得到L函数，而不使用方程呢？

看看这个：

我所做的是将这个序列写在顶部，然后遵循一个程序。这个程序是一个循环，先减去，然后复制结果。

取第一个顶部元素1，减去下面写的所有内容，下面没有东西，所以1减去没有东西就是1，然后将1的副本分布在第一行：

在第二列，取顶部元素1，减去下面所有内容。1-1就是0，然后将0的副本分布在第2行，以2为间距。

第三列，取顶部元素0，减去下面所有内容。0-1=-1，然后将-1的副本分布在第3行，以3为间距，依此类推。

第四列，有1-1-0=0，

第五列，得到的是2-1，也就是1。

然后0减这些数字，就是0，依此类推。

让我们继续：

你看到规律了吗？看看对角线：

1、0、-1、0、

1、0、-1、0、

1、0、-1、0。

这就是规律。我们现在可以用这个简单的周期性对角线重构L函数，只需按相反的方向操作。所以我首先填写对角线，然后像之前一样在行中分填写副本，减法的反操作是加法，所以我只需要将每一列向上求和就可以得到顶部的元素。1的和是1，1和0的和是1，1加-1是0，1加0加0是1，1加1是2，依此类推。

这样，我们根本没有使用方程K，我们用一个更简单的对象，即对角线，重构了L函数。

现在这个对角线实际上是一个automorphic L函数。它是自然界中最简单的自守L函数之一，我们使用这个automorphic对象，以某种意义上与黎曼zeta函数一起，重构了原始的Motivic L函数，其中系数是1、1、1、1、1、1、1、1、1、1。

E的神秘之处

朗兰兹计划。我们需要再给出一个例子。回想一下从方程E得出的序列。方程是：

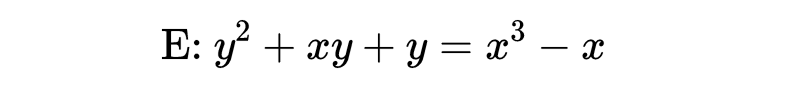
L函数是：

这台机器接受一个方程，给出一个序列，这在前面的例子中使用高斯整数的计数描述。在这个例子中，我将用不同的语言描述同样的机器。

现在我们将对不同的质数p进行模p解方程的计数。

对于任何正整数m，每当有一个带有整数系数的多项式方程时，就可以计算模m的解的数量，我们从模2开始。

在这个例子中，先对方程的两边进行因式分解会更快。

模2意味着x和y只能是0和1。所有的计算都是在模2下完成的，所以例如1+1=0。

右边总是零，因为x或者x加1都是0。

因此左边也必须是零，那么可能是当y为0时，然后x可以是任何值，0或1。

或者，如果y是1，那么括号里的值必须为零，这只有在x为0时才会发生。

总的来说，模2下有三个解：

当y为0时，x可以是任何值，当y为1时，x为0。而解的数量，3，正是我们想要找的。

现在让我们计算模3下的解的数量。

x和y将是0，1或2。

所有的计算都是在模3下完成的。右边是三个连续整数的乘积，其中一个会是0。因此整个乘积都是0，所以左边也必须是0。现在，要么y是0，x可以是任何值，要么y是1，那么括号里的必须为0，这意味着x是1。最后，y可以是2，那么x必须是0。

总的来说，有五个不同的解符合模3的方程。

下一个质数是5，解的计数类似，只是更多的分类工作。模5下会有5个解。

把这些情况做成一个大的表格：

第一行是n：1、2、3、4、5、6、7、8、9等等。第二行是质数p：2、3、5、7、11、13。在这些质数下面是解的数量。模2有3个解。模3有3个解等等。

我们的目标是从这些解的数量中构造出L函数，将这个过程分为三步。首先对于质数，只需用质数本身减去解的数量。2减3等于-1，3减5等于-2，5减5等于0等等。最后一个是13减17，等于-4。

对于任何方程，可能会有某些质数不同。我们称它们为坏质数，对于这个方程E，可以计算出，坏质数是2和7。我在这里没有展示计算过程。

第二步，对于质数的幂。对于2的幂（1、2、4、8），2是一个坏质数，对于坏质数的规则是，质数的幂对应的值应该是一个几何序列，从1开始。所以有1、-1，然后再有1，然后-1，这会在2的所有幂之间交替出现1和-1。

对于3的幂，3是一个好的质数，规则稍微复杂一些，但是有一个递归公式可以求出3的幂对应的值，这在本例中为取-2（3对应的值）的平方，也就是4，然后减去质数3。这得到了9的值为1。

第三步，对于剩下的n的值，通过乘法性来计算。例如，对于数字6，6是2乘以3，所以为了计算我需要的数字，需要取-1（2对应的数字）乘以-2（3对应的数字），得到了2。对于10，10是2乘以5，需要取-1乘以0，得到的是0。最后，如果我将12分解为质数的乘幂，得到的是4乘以3，所以需要取-2乘以1，得到了-2。

最终的结果是：

现在，我们已经从不同质数模下的解计数中构造出了L函数。这个过程几乎适用于任何方程。首先是质数，然后是质数的幂，然后是所有其他的数字。

但是仍然面临着和前面的例子中一样的两个主要挑战。首先，有没有一种规则，可以计算出序列中的下一个元素，其次，有没有一种方法可以直接得到L函数，而不需要使用方程？

这里需要借助一些“硬币”来解释接下来的问题。

红色硬币的面额是1、2、3、4、5、6、7……

蓝色硬币的面额是2、4、6、8、10、12……

黄色硬币的面额是7、14、21、28……

绿色硬币的面额是14的倍数。

规则是每种类型的硬币都有无限多。

假设我要给你1块。有多少种方式？只有一种方式，给你一枚红色的一块钱硬币。

假设我要给你2块。有多少种方式？

可以给你两个红色1块钱，或者一个红色的2块钱，或者一个蓝色的2块钱，一共有3种不同的方式。

那3块钱呢？

有4种不同的方式。

将所有这些组合情况放入一个表格中。

从0块钱开始，只有一种方式，那就是不给你任何硬币。2块钱3种方式，3块钱4种方式，然后是9、12、23、32、55、76、122等等（这是一个斐波那契数）。

下面是一个通常的乘法表：

也许你会说这很无聊，但是看看对角线之和：

他们是1、4、10、20……。让我们用两个规则来构造一个新的、更令人兴奋的乘法表。

首先，一边是这些硬币组合计数，1、1、3、4、9、12、23。第二个规则，对角线之和应该是序列：1、0、0、0、0、0、0、0……

第一个对角线之和应该是1，所以我这里需要一个1。这意味着我必须把1放在顶部，因为1乘以1是1。然后是1乘以3是3，1乘以4是4，等等：

现在第二个对角线之和应该是0。

这意味着第一行第二列是-1，然后顶部应该是-1。这样可以填写出第二列：

最终的结果是：

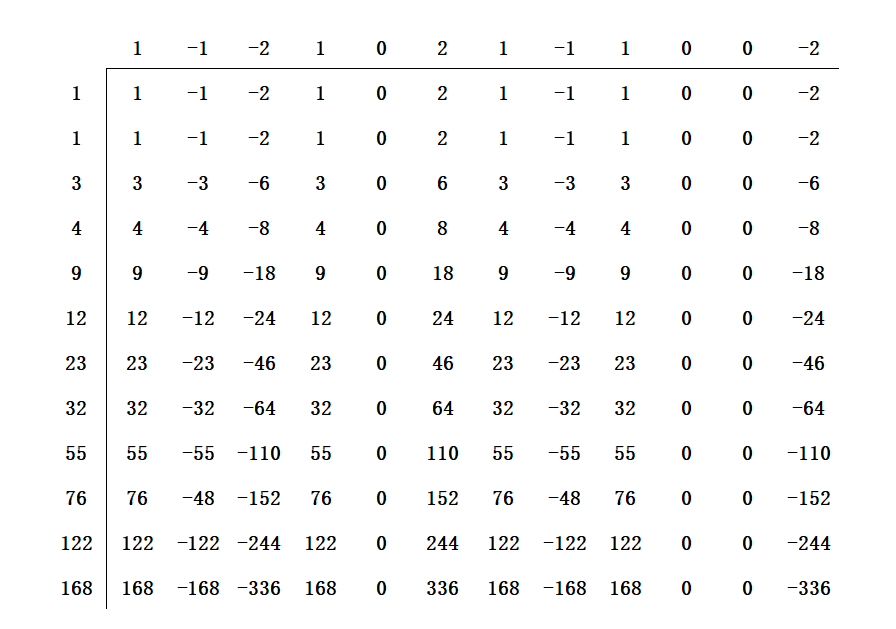
我们已经使用硬币构建了L函数，并且再次，这个过程的引人注目的地方在于，我们构建了E的L函数，却完全没有使用方程。

现在，你可能会说，对于更大的n，比如20块钱，组合的数量超过3000个，这种硬币计数变得非常耗时。

但是，我们可以用生成序列的语言来重新描述这个硬币问题，有了这个工具，就很容易计算很大的数。这个L函数的生成序列是：

总结一下，我们可以从方程E中得出L函数，也可以通过完全不同的方法构建它。

实际上，这个生成序列是一个automorphic 对象。更准确地说，它是一个模形式（modular form），它给你的L函数与方程相同，而方程是一个椭圆曲线（elliptic curve）的例子。

关于朗兰兹计划

我想谈谈更大的图景。

今天的朗兰兹计划，包括了令人眼花缭乱的许多不同的分支，但原始的主要分支，直接与L函数相关，可以被称为全局数域（Global number fields），而这个主要分支包括两个主题。

一个主题是函子性（Functoriality）；另一个主题是互惠性（Reciprocity）。互惠表达的想法是，任何motivic对象都有一个相应的automorphic 对象，具有相同的L函数。对应关系的两侧的对象都有一个维度，有时被称为秩。朗兰兹的互惠是关于任何维度的对象的声明，1、2、3、4、5等等。椭圆曲线和模型形式之间的对应关系，因为费马大定理而相当出名，是二维朗兰兹互惠的一部分。这就是我们想通过第二个例子，称为E，来表达的。

在一维，朗兰兹互惠包括了被称为阿廷互惠（Artin reciprocity）的东西，阿廷互惠的最简单情况是二次互惠，高斯发现的。他称之为黄金定理。我们今天的第一个例子，K，是二次互惠定律的一个特殊的案例，所以在某种意义上，它是一维朗兰兹互惠的最简单的案例。如果你想读一些关于朗兰兹计划非常易于理解的东西，我会推荐Edward Frenkel写的这本《Love and Math》，它是令人难以置信的美丽。