在你的中学物理课堂中可能遇到的所有系统中，最重要的无疑是简谐振荡器（the simple harmonic oscillator），它是一个质量方块连接到弹簧的基本装置。

从经典力学到量子力学再到量子场论，没有其他系统如此深入地渗透到物理学的各个角落。

但是为什么这个看似微不足道的问题在如此多的物理领域中无处不在呢？这就是我想在这篇文章中解释的。我们将从基本设置开始，然后讨论为什么它如此重要。

有一个质量为m的方块放在一个无摩擦的桌子上。它连接到一个弹簧，弹簧的另一端固定在墙上。如果你轻轻推一下这个方块，或者拉开一段距离然后放手，它会像正弦或余弦函数一样来回摆动。我们称这种振荡为简谐运动。

使用牛顿定律，可以这样理解：每当方块移动，它就会拉伸或压缩弹簧，因此，弹簧会试图将方块拉回或推回到其平衡位置。

平衡位置是弹簧既不受压也不拉伸的位置，因此不会对方块产生力。假设将弹簧拉离平衡位置x距离，弹簧将方块拉回平衡位置的力与x以及弹簧的刚度成正比，刚度由另一个参数称为弹簧常数k衡量。因此，力为F=-kx，而方块的F=ma方程可以写为ma=-kx。我们可以通过将m移到右侧使其看起来更整洁，并定义一个新符号表示k/m这个出现的分数，

同时，加速度a只是位置x(t)关于时间的二阶导数，因此我们可以将F=ma方程表示为

这意味着为了求解方块的轨迹，我们只需要求关于时间t的函数x(t)，连续两次取其变化率后，得到，

正弦和余弦正是具有这种性质的函数，因此这个方程的一般解是

其中A和B是取决于t=0时方块状态的数，即方块离平衡位置的距离。因此，方块以简谐运动的方式在其平衡位置附近正弦振荡。它振荡的速率由Ω决定，因此我们称之为系统的自然频率（naturalfrequency）。注意，Ω是由弹簧的刚度和方块的质量确定的，无论如何设置方块移动，它总是会以相同的速率振荡。

在我们了解为什么这个简单系统如此重要之前，还有一个需要知道的知识，那就是弹簧的势能。

当方块来回滑动时，它的速度不断加快或减慢，因此其动能一直在变化。但是，如果加上弹簧中存储的势能，那么总能量就是一个常数。

我们可以通过求E的变化率来检查这一点，

在第一个项中，我们将2的幂降下来得到m乘以v，然后由链式法则，需要将其乘以v的变化率，即加速度a，得到

同样，在第二项中，我们再次将2降下来得到kx，然后将其乘以x的变化率，即速度v，得到

所以，

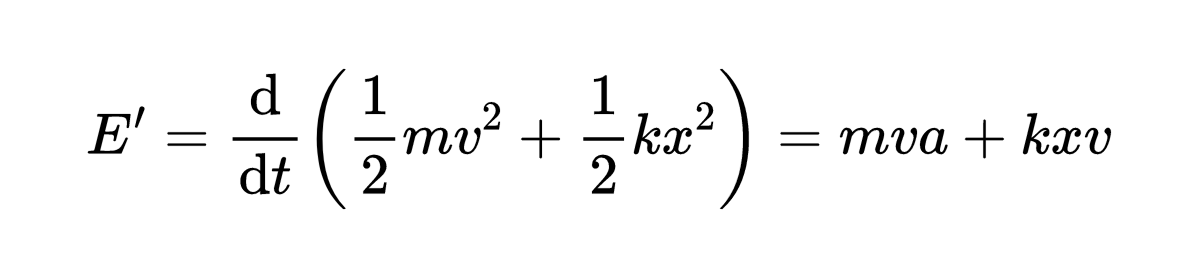
现在，我们将这个共同因子v提取出来，括号中的内容将因为F=ma=-kx而消失，

因此，总能量是一个常数。注意力F=-kx与势能U=1/2 kx²之间的关系是

换句话说，力等于势能曲线的负斜率，这是力和势能之间的一般关系。

这意味着在平衡状态下，当力等于零时，势能的斜率必须消失。实际上，你可以将势能曲线视为一座无摩擦的山，

一个粒子沿着它滑动。在简谐振子的情况下，山是一个抛物线形状，平衡点位于山谷底部。如果将粒子放在x等于零的地方静止，它将永远待在那里。然而，如果将粒子放在离平衡位置较远的地方，它将在山谷底部来回摇摆，就像方块在其平衡位置附近来回振荡一样。

将势能曲线视为这样一座山是一种非常强大的方法，可以迅速发展出对一个处于一般势能中的粒子行为的直观认识，而无需进行F=ma方程求解的繁琐工作。

面对一个非常复杂的势能，我们无法写出粒子轨迹的简单解，但我们仍然可以通过将势能想象成一座山来定性地理解粒子的行为。这就引出了为什么简谐振子如此重要和广泛的原因。

考虑一个在任意势能U(x)中运动的粒子，这是一个随机示例。我们希望再次决F=ma方程，以确定轨迹x(t)。

但对于这样复杂的势能，寻找一个简单的解几乎不可能。那么我们该怎么办呢？首先，当你有一个势能曲线时，你应该做的第一件事是确定其平衡点。平衡点是指粒子上的力为零，因此势能的斜率在那里为零。稳定的平衡点是位于谷底的一个点，而不是山顶。

当然，对于一个放置在平衡点上静止的粒子，我们可以写出F=ma方程的精确解。

另一方面，如果你推一下一个处于稳定平衡的粒子，它会在势能底部来回摆动。如果你留意的话，你会发现在日常生活中经常会看到这种现象。当你轻轻地摇晃椅子时，它就在稳定平衡点附近摆动。

挂在钩子上的外套也会在其平衡轴附近轻微摆动。基本原因是，在几乎任何势能的稳定平衡点附近，山底看起来就像简谐振荡器的抛物线。

这不仅仅是一个粗略的定性类比，我们可以使其在数学上精确，即使用泰勒级数在稳定平衡点附近将任意势能U(x)展开为x的幂次，

如何去理解（看待）这个级数展开？首先，如果你正坐在x=0的位置，那么当你计算势能时，显然会得到U(0)，

然后，如果你离开那里走一小步，使x成为一个小但非零的数字，势能仍然接近U(0)，但现在它会被斜率U'(0)乘以位移x稍微移开，

这已经是在给定点附近大多数函数的一个很好的近似值，但实际上，在这种特殊情况下，它对我们没什么用，因为我们已经将原点放在了U(0)和U'(0)都为零的平衡点上。

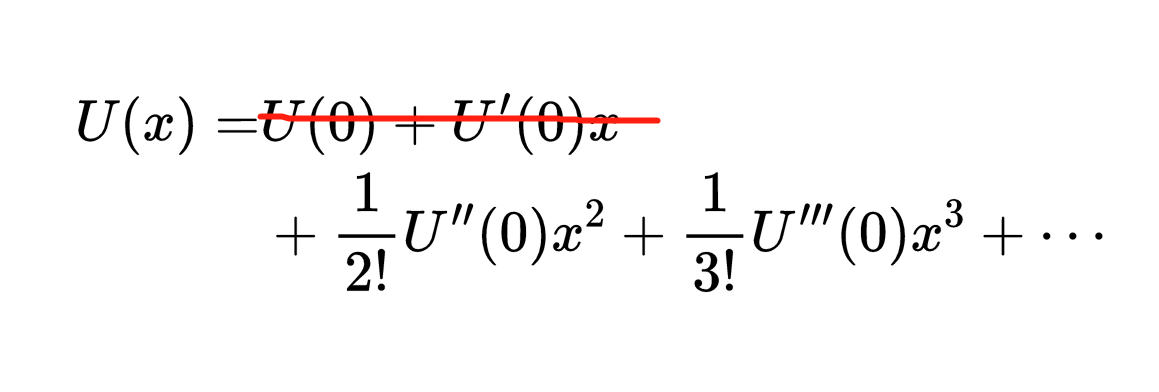
为了得到更好的近似，我们必须在泰勒级数中包含具有更高x次幂的项。通过包含越来越多的这些项，我们可以得到一个更好的近似函数。

当我们加上所有无穷多的项时，将重现精确的函数。但是，我们不需要无穷多的项来获得在稳定平衡点附近的势能的良好近似，只需要第一个非零项，即二次项

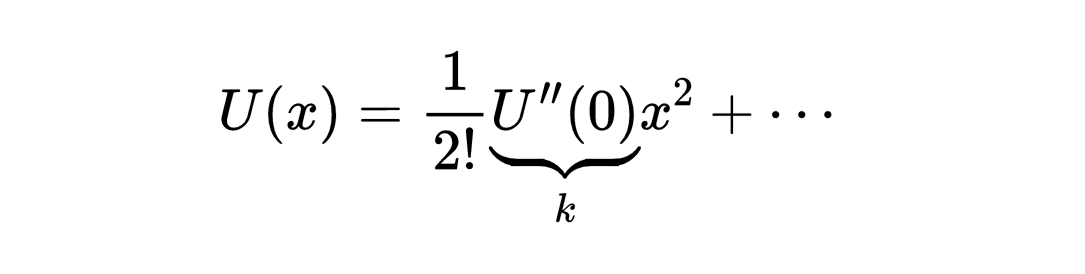
但这是具有弹簧常数k=U''(0)的弹簧的势能。这就是关键所在：几乎任何势能函数，无论多么复杂，在其稳定平衡点附近都会简化为简谐振荡器势能。

这就是为什么简谐振荡器如此普遍：系统倾向于趋向稳定的平衡，小的扰动会使它们在平衡附近摆动。因此，我们应该首先找到任何势能函数的稳定平衡点，然后询问当它稍微偏离平衡点时会发生什么。在平衡点附近的粒子将以自然频率围绕平衡点进行简谐振动，即

理解远离平衡点的物理现象通常要困难得多。x越大，泰勒级数中的高次修正项，如x^3和x^4，就越重要。但是，我们通常可以通过将这些修正项视为简谐振荡器解的扰动来获得近似解。所有这些内容可能听起来很熟悉，也可能听起来很陌生，但如果你之前研究过单摆，那么你已经看到过它们在实际中的应用。

如果一个摆在角度θ处倾斜，其中杆的长度为l。

其势能为U = mgh。将质点沿弧线轨迹的弧长坐标记为s，使得θ = s / l，那么我们可以将势能写为

它的图像是这样的，

稳定平衡点在中间，即s = 0，单摆直挂静止。我们可以通过对势能求导来进行检查：余弦的导数是负正弦，然后从链式法则得到1 / l，得到

如果代入s = 0，得到sin(0) = 0。同时，

如果代入s = 0，我们得到

注意它是正的，这说明它处于稳定平衡状态。所以围绕平衡点的泰勒展开是

如果将U'' = mg / l代入，我们得到一个具有该弹簧常数的简谐振荡器，

围绕平衡点振动的频率是根号(k / m)，你可能认为这是单摆频率的熟悉公式。在这种情境下，泰勒展开通常被称为小角度近似，因为它相当于在θ = 0附近展开单摆的F = ma方程。

在这个邻域内，系统简化为一个简谐振荡器，所以单摆在平衡位置附近正弦振荡。