
假设我掷一对骰子,然后你下注两个骰子的和是多少,你会选择什么?明智的选择是7,因为两个骰子加起来为7的组合最多。

其实,你可以将同样的逻辑应用到预测宇宙的行为上。让我们来看看物理学中最强大的工具如何真的就像一场宇宙级的赌博游戏。
在19世纪,科学家们忙着找出一系列的法则来将物质的性质相互联系起来。通过将温度、压力和流体体积等联系起来,他们发现了热力学定律。但这些定律的起源却让那些科学家们困惑不已。当他们意识到物质是由原子和分子组成的,以及热力学性质和定律是由这些粒子的运动和相互作用产生的,事情开始变得更有意义。
我们不能将运动定律应用到每一个空气分子上来计算一个房间中的气体行为,因为分子数量实在太多。但幸运的是,我们并不需要这样做。只需理解粒子运动的统计特性,就可以预测它们的行为,这正是统计力学领域所做的,但统计力学也做出了超越19世纪物理学家想象的惊人预测。


它预测了超流体(superfluids)和超导体(superconductors)等非常奇特的物态的存在,甚至预测了恒星在“死亡”时会塌缩成黑洞。
让我们开始一个实验:

有一个真空的房间,没有重力,在其中射出一百个弹球。每个球都很小并且具有完全的弹性,以某种随机的角度和速度射入。球足够小,以至于它们永远不会互相碰撞,但却可以在不失去任何能量的情况下在墙壁上反弹。它们也移动得足够快,以至于很快就充满了整个房间。

让我们只关注其中一个弹球。如果知道它的初始速度和方向,就可以确定它的路径。但是,如果我们不知道它的初始速度和方向,那么它的位置看起来将是随机的。实际上,如果允许无限的反弹,那么这个球可能出现在房间的任何地方,各个位置的可能性基本相等。所以,这100个球可能排列成一个完美的晶格,可能毫无规律地(随机)散落在房间的各个角落。
无规律地弥散在房间中看起来最有可能,但实际上,任何特定的球的排列方式的概率是相等的。我们更可能看到一个看起来随机的分布,只是因为随机分布的方式,比规律分布的方式多得多。

为了更容易理解这一点,让我们将房间划分成10个盒子。将球投入房间相当于随机将它们投入这些盒子中。我们更可能得到一个相对平均的分布,而不是它们全部落在同一个盒子里。

但是,如果给每个球贴上标签,并指定每个球属于特定的盒子,那么每个球随机落入其预分配的盒子的机会就和所有球落入同一个盒子的机会一样小。两者的概率都是1除以10的100次方。

我们可以用同样的思想来考虑房间中的气体分子的状态,但现在有10的27次方个粒子而不是100个,所以得到任何一个特定分布的概率都是极其微小的。同时,气体分子大致均匀分布在房间内的情况远远多于更有序的情况。
在统计力学中,我们将气体分子的每一个特定分布情况称为微观状态,而分布的大致形状(分散或聚集)称为宏观状态。宏观状态代表了可观察的性质,通常是热力学性质,如温度、压力和体积。微观状态代表了隐藏的性质,如每个粒子的位置,每个宏观状态都对应许多可能的微观状态。
我们几乎总是观察到世界处于与最大可能数目的微观状态接近的宏观状态。一个系统的每一个可能的微观状态(即给定的粒子配置或能级分布)都被赋予相等的概率。然而,一些特定的宏观状态对应的微观状态的数目远远超过其他的宏观状态。因此,系统在任何给定的时间点上都极有可能处于这些"最可能"的宏观状态。
例如,考虑一个简单的系统,如理想气体在容器中的分布。尽管理论上有可能所有的气体分子都偶然地聚集在容器的一角(这将是一个非常罕见的宏观状态),但我们几乎总是观察到气体分子均匀分布在整个容器中(这是一个非常常见的宏观状态),因为这个宏观状态对应的微观状态的数目非常多。
这就是为什么我们几乎总是观察到世界处于与最大可能数目的微观状态接近的宏观状态。这也是热力学第二定律中熵增加的原理:系统总是倾向于进入熵更高(即可能的微观状态更多)的宏观状态。
回到弹球,假设它们也可以相互反弹。当它们在房间内移动时,它们的位置改变,同时它们在碰撞时速度也改变,并且与其他球交换能量。我们可以像考虑位置分布一样来考虑它们的能量分布。
将球可以拥有的所有可能能量分成一系列能量箱,球的能量分布就是每个能量箱中的球的数量。就像位置一样,球在互相作用时会在能量箱之间移动,就像在位置空间一样,随着时间的推移...系统将探索这个能量空间的所有可能配置。
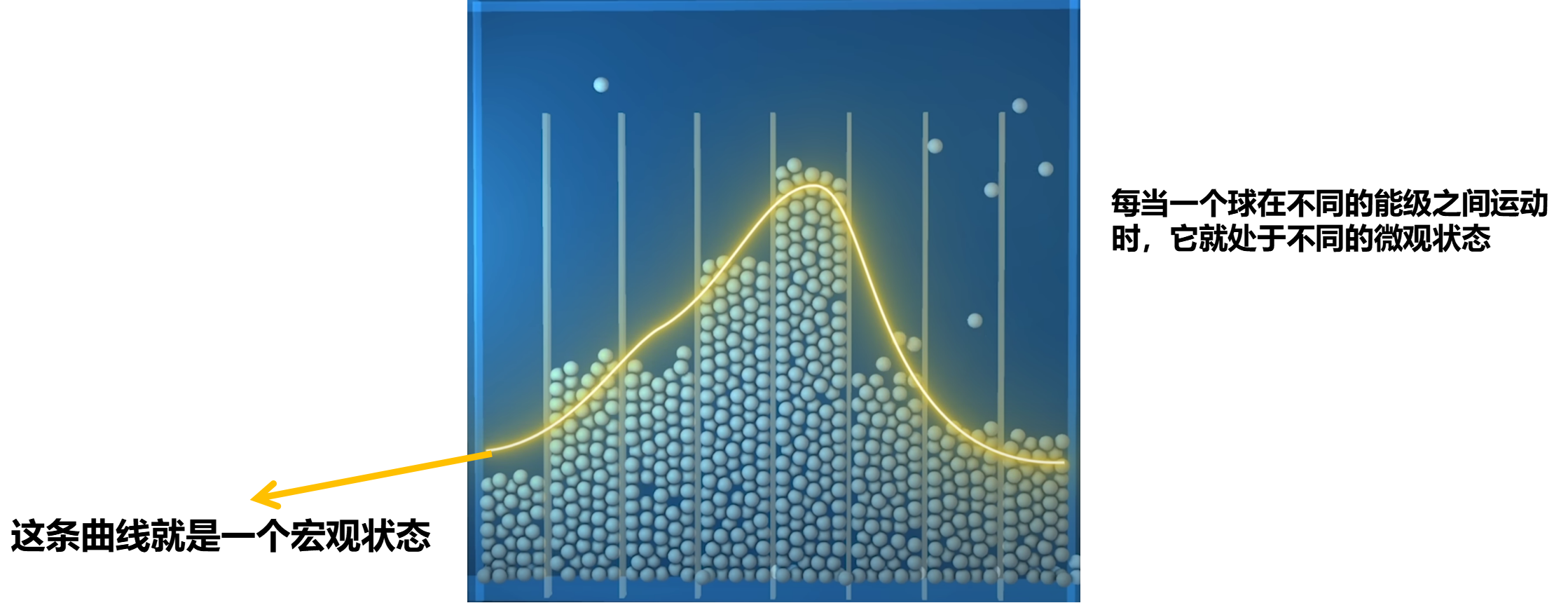
每个特定的能量分布再次是一个微观状态,而宏观状态是整体能量分布的特定形状。例如,这些是不同的宏观状态,

而且我们极有可能观察到的宏观状态和能量分布,是由最大数量的微观状态导致的。球的位置倾向于在房间内均匀分布,球的能量也受到约束,但方式不同,因此,能量分布并不是在所有可能的能量上都是平均的。
能量是守恒的,如果一个球失去能量,另一个球就会得到相同的能量。你可以以各种方式将粒子在其能量箱中排列,以得到相同的总能量,例如这样,

或者将它们全部堆积在对应平均能量的箱子中,

这些分布可以通过在基本扩散范围内交换球来建立多个不同的微观状态。但是有一个特定的能量分布,允许最多的交换,有最多的微观状态。就像这样,

这是麦克斯韦-玻尔兹曼统计结果的能量分布。在数学上,它看起来像这样,

它告诉我们每个能量箱中的粒子数量,它取决于物质的温度。从这里我们也得到了粒子速度的分布,

这被称为麦克斯韦-玻尔兹曼分布(Maxwell-Boltzmann Distribution),所有这些真的只是来自我们随机地将球放入不同能量箱的方式的数量。
麦克斯韦-玻尔兹曼分布代表了最大的混乱,或者说是能量分布的最高熵。就像高熵由粒子以随机的方式填满房间表示的一样。
为了给你一些关于为什么它看起来像这个歪曲的钟形曲线,而不是平均分布的直觉,考虑一下之前的骰子。最常见的数字是七,那只是因为你可以用最多的方式掷出它:1和6、2和5、3和4、4和3、5和2、6和1。每一个这样的数字组合都是一个微观状态,所有的微观状态都对应于掷出七这个宏观状态。下一个最常见的宏观状态是六和八,每个都有五种方法可以掷出。
目前为止,我确实忽略了一个非常重要的东西。当我在计算实体状态时,我假设将球放入其能量箱的顺序很重要。这没问题,如果球彼此互不相同。但是,如果球无法区分,那么简单地将两个粒子互换位置不应计算为两个不同的微观状态。这意味着我们在计算状态时过度计数了。
当我们正确计算状态时,得到的能量分布方程是这样的,

它是由玻色和爱因斯坦在1925年共同发现的,因此这种统计被称为玻色-爱因斯坦统计(Bose-Einsteinstatistics)。任何以这种方式行为的粒子类型都被称为玻色子,所有的玻色子都
彼此无法区分,
并且能够无限量地堆积在任何给定的能量箱中。

这减1在大多数情况下几乎没有任何差别,所以我们经常只是使用麦克斯韦-玻尔兹曼公式。
但是,当这个减1变得重要时,它也真的很重要。对于具有极低能量的系统,它导致每个能量箱中的粒子数量有巨大的不同,使得可以在最低能量状态中塞入更多的粒子。这产生了一种全新的物质状态——玻色-爱因斯坦凝聚态(Bose-Einstein condensate),它在超导、超流动和根据材料的不同表现出各种奇特行为。
最后,我们以一种导致玻色-爱因斯坦和麦克斯韦-玻尔兹曼统计行为截然不同的方式计数状态来结束。
每个能量箱中的粒子数量没有限制,但并非所有粒子类型都是这样。一些粒子拒绝分享他们的能量箱,所以每个能量状态只能被一个粒子占据。就好像在一个骰子上掷出1,意味着另一个骰,不能掷出1。

我们需要以非常不同的方式计算这种粒子的可能状态,结果是费米-狄拉克统计(Fermi Dirac statistics)。

遵守这些统计规则的粒子被称为费米子。费米子是无法区分的,并且他们每个能量箱只能有一个。
简而言之,具有半整数量子自旋值(如1/2、3/2、5/2等)的粒子由于量子力学原理禁止重叠。这些粒子是费米子,包括构成大部分物质的粒子,如电子、质子和中子。整数自旋(如0、1、2等)的粒子是玻色子,包括像光子这样的力携带粒子。但是,你也可以通过将自旋为1/2的费米子组合起来制造出玻色子,例如氦-4原子。
费米-狄拉克统计看起来与其他统计类型相似,但现在玻色-爱因斯坦的负号变成了正号。对于高温,这个变化很小,但在低温下,事情变得很奇怪。因为费米子不能全部落入单一的最低能量状态,它们反而填满了所有可用的低能量状态,每个状态一个粒子。这导致了像原子中的电子只能有一个电子在每个能量壳层这样的事情。实际上,由于电子的自旋允许最多两个电子彼此区分,且自旋方向相反,所以每个壳层有两个电子。
但结果是,如果电子是玻色子,原子会比现在大得多,这就是宇宙中有化学和结构的原因。费米-狄拉克统计的奇特行为也导致了宇宙中一些最奇特的物体,如白矮星和中子星,其中所有的最低能量状态都被填满,产生了我们所说的简并物质。这些物体只能通过他们的费米子不能再靠近来抵抗引力崩溃。
使用费米-狄拉克统计,我们计算出了一颗恒星需要多大的质量才能通过白矮星阶段和中子星阶段坍缩成为黑洞。关于统计力学,我现在要说的就这些。它全在于计数。我们感知到的是宇宙的粗略属性,其细节被隐藏在我们的视线之外。但只要我们数一数那些粗略的可观测性质可能产生的不同的隐藏方式,我们就能在预测这些可观测性质的行为方面获得巨大的力量。
通过掌握宇宙骰子游戏,我们对物理定律的起源有了新的理解,就像在空间时间表面之下掷骰子一样。