
在一个特定大小的网格上(最多)放置多少个点,使得没有三个点在同一直线上?这竟然是一个未解决的问题。但与一些看似简单实则困难的问题不同(比如Collatz猜想),这个问题上已取得了一些进展。看看这些进展,也许还可以深入了解如何处理数学中的开放问题。一起探索吧!
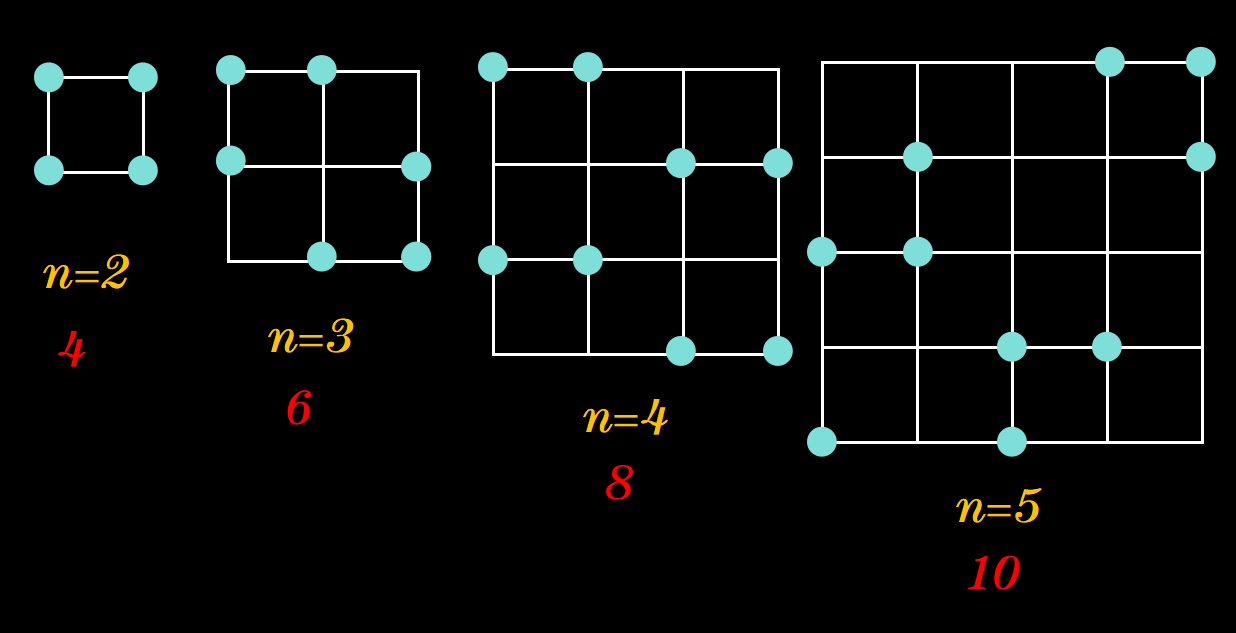
首先,从一个正方形网格开始,有n行n列。对于给定大小的网格,可以在网格线的交叉点放置多少个点,以确保没有三个点可以用直线连接?

这个“三点不同线(No three-in-line problem)”的问题最初由Henry Dudeney在1900年提出,当时是关于一个8x8的棋盘上的棋子。

解决这类数学问题的一个有效方法是先观察n较小的情况。可以从小的网格开始,你会注意到,当n增大时,问题逐渐变得困难。n为1和2的正方形可以完全填满,但从3开始,就需要一些技巧。当n=4时,开始有多种不同的方法可以达到最大值,

而在n=5时,必须开始考虑“象步”对角线:

对于n=5,这里有一个可能的解:

上界
当n较小时,可能遇到的第一个障碍是不知道什么时候停下来。我们如何知道已经放置了所有适合的点?如果能有一个上界就好了:即使不确定能达到那个数字,但确信不能超过那个数字。

是时候用一般的数学规则来求解问题了。当n较小时,能放置的最多的点的数量是网格的宽度乘以二。
事实证明,我们可以用称为鸽笼原理(pigeonhole principle)的规则来证明我们永远不会做得更好。
鸽笼原理说,如果有n个对象被放入k个空间中,那么至少存在一个空间,其中有n/k或更多的对象。

假设有5个鸽笼放16只鸽子。如果试图使每个鸽笼中有3只或更少的鸽子,那么只能容纳最多15只鸽子,所以有16只鸽子时,至少有一个鸽笼中必须有4只或更多的鸽子。

如果只关注正方形网格的行,并忽略列和对角线,那么可以把点当作鸽子,行当作鸽笼。每一行本身就是一条线,根据规则,每行最多只能有2个点,这意味着在一个n x n的网格上,最多只能放2n个点。
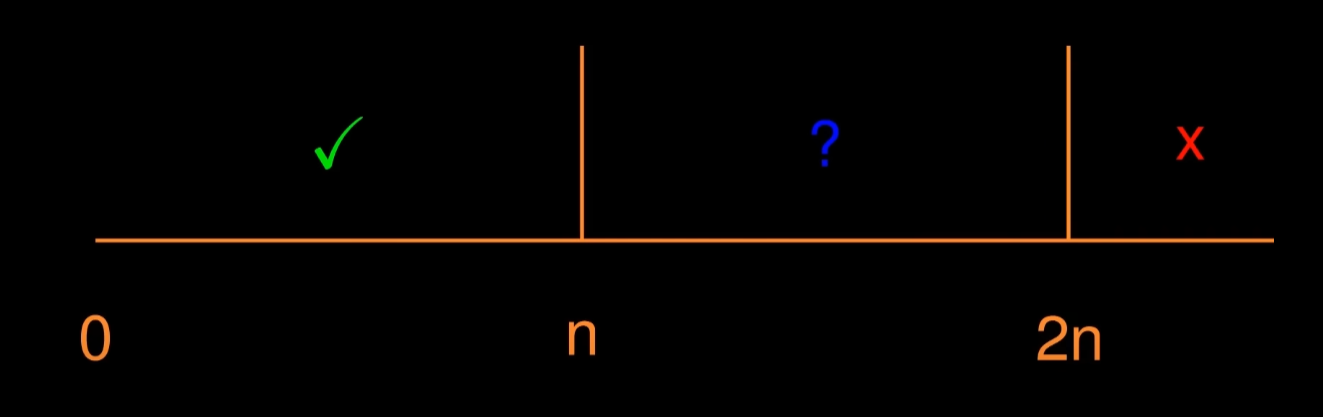
所以我们找到了一个上界,但我们现在还不知道当n取任意值时,是否总能达到这个上界。实际上,我能找到的最大网格是n=52,在上面最多放2n(104)个点,使得没有三个点在同一直线上。

下界
可以使用越来越强大的计算机搜索越来越大的网格,但在数学中,我们更喜欢一般的情况。那么,对于n非常大时应该怎么办?比如n=1000或者更大呢?我们已经有一个上界。也许我们可以找到一个下界。
文献中出现的第一个下界来自极其多产的数学家保罗·埃尔德什(Paul Erdős)。

埃尔德什发现,对于任何质数 p,总能在 p x p 的网格上放置至少 p 个点。埃尔德什证明这一点的方式揭示了另一个有用的解决问题的技巧:用数学的另一个分支重写问题。埃尔德什将这个几何问题转化为一个数字问题。我们现在来看证明:
首先在方格上放置 x 和 y 坐标,例如从0到 p-1的整数。埃尔德什说我们可以在每一列中选择一个点,以确保这些点中的任何三个都不在一条直线上。方法是:为了找到 y 值,取 x 值,然后求它的平方,并求除以 p 之后的余数。

所以我们找到的点是沿着函数 y=x^2 mod p 的点。
我们怎么知道这种方法总是有效的呢?在网格内取 y=x^2 mod p 上的任意三个不同点。我们称这些点的 x 坐标为 i、j 和 k,按递增顺序,所以这些点的完整坐标分别是(i, i^2 mod p)、(j, j^2 mod p)和(k, k^2 mod p)。

第一点和第二点之间的线的斜率就是:

同理,第一点和第三点之间的斜率是:

如果这三个点在同一条直线上,这些斜率必须相等:

如果可以从这些分数中消去 j-i 和 k-i 就太好了,但我们要小心,某些数字mod下除法可能会有奇怪的事情发生。比如:

消去(4-1)后的答案是5,但实际答案是0。但在某个数字m下的除法在某些特殊情况下确实可以消去。

特别地,如果被除数、除数和商都要求为整数,且b与m除了1之外没有公共因子,也就是,b和m是“互质”的。
在我们的网格中,因为p本身就是质数,所以p与所有不是p的倍数的整数互质。由于 j-i 和 k-i 小于 p,它们不能是p的倍数,而由于 j+i 和 k+i 是整数,这意味着我们可以放心地进行这些消去操作。 最终得到 j=k。但我们最初假设 i、j 和 k 都是不同的!所以,得到了一个矛盾,意味着这一组中没有三个不同的点位于同一条线上。所以,埃尔德什的方法对一个质数大小的网格总是有效的。
对于质数n找到这个结果更有帮助:我们知道至少可以在 nxn 网格中放入至少与小于n的最大质数一样多的点,其中没有三点共线。所以对于1000x 1000的网格,最多放入的点的数量至少是997。而且,正如 Joseph Bertrand 所提出的,Pafnuty Chebyshev 所证明的,对于 n>1,总是存在一个介于n和2n之间的质数。所以,我们至少总是可以在nxn网格中放入至少 n/2个点,没有三个点共线。

更好的下界
模数运算使得 Richard R Hall 和他的合著者在1974年进一步提高了下界。我们将从视觉上看这些结果,但我们不会完全证明它们。他们的论文比埃尔德什的证明难以理解,但如果你想了解,论文题目是“Some advances in the no-three-in-line problem”。
作者首先证明,无论n是否是素数,任何n x n网格上都可以放置至少 n 个不共线的三点。
使用贝尔特兰和切比雪夫的定理在 n/2和n之间选取一个素数p。方程 xy mod p = -1给出了一组 S 中的 p-1个不在一线的点,这些点位于 p x p 的网格中,而且没有两个点共享同一行。

我们可以通过将直线的方程 y=mx+b 代入方程来证明这一点。这产生了一个二次方程,


其最多有两个解,对应于 S 中的线上最多两个点,这些点在 mod p 下不等价。此描述隐藏了许多模运算法则,但 Hall 和他的朋友们证明了所有的细节。然后我们可以取 S 的两个副本,

再加上一个额外的((p-1, p+1),然后将那些 2p-1 个点的前 n 个放置在 n x n 网格上。其次,他们证明,对于任何素数 p,一个 2p x 2p 的网格可以容纳 3p-3 个点,或稍少于1.5n。
取这组S中的 p-1个点,将其分为四个四分之一网格,

并将这些四分之一网格分别复制3次,围绕 2p x 2p 的网格排列。

这个大集合 T 包含了 S 中每个点的三个副本,这些点在 mod p 下是等价的。按照之前的逻辑,T 中的三个点只有在至少两个点在 mod p 下等价的情况下才能在一条线上。这只能发生在一条水平的、垂直的或者斜率为±1的线上。

水平和垂直线不能包含3个点,因为它们只经过S的2个副本,而对角线也不能,因为它们经过的第三个点会在T的中心“空隙”中。
所以,我们已经得到了大约1.5n 的下界和 2n 的上界。

但是,我们还不确定在那个范围内可以找到任何特定的大 n 的最佳解。还有最后一个解决问题的技巧——猜想(conjecture),来自 Richard Guy 和 Patrick Kelley 在1968年,由 Gabor Ellmann 在2004年修正。
这个猜想使用了统计参数。首先,我们需要计算在 n x n 网格中3个随机点是共线的概率。Guy 和 Kelley 用组合数来做这个(也就是非常高级的计数),如果你想看所有的细节,你应该查看他们的论文(The No-Three-In-Line Problem)

诀窍是计算所有可能斜率的所有直线上的所有点。

得到的大致概率是
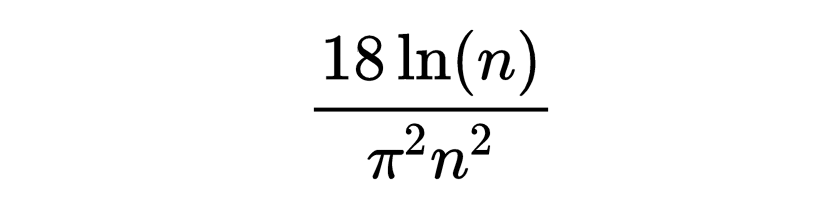
一旦有了这个概率,就可以计算,对于任何给定的常数 k 在1.5到2之间,一个 n x n 网格中随机选取的 kn 个点没有3个点共线的概率是多少。结果大约是

然后,乘以 kn 点的总组合数,
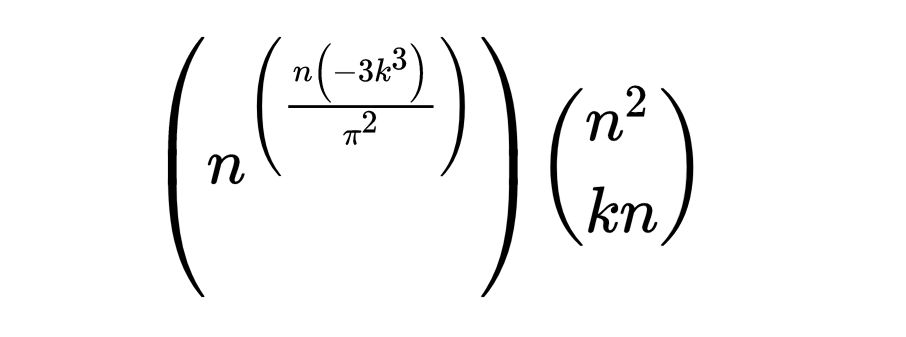
来看大约有多少没有三点共线的组合。这个等式是由一个 n^n 项支配的,或者更具体地说是

这实际上是 Ellmann 的修正所在:Guy 和 Kelley 错误地使用了 +2而不是 +k。当指数中的系数为负时,这个项变为零:换句话说,如果 k 太大,那么,我们预计基于随机性,可能没有任何三点共线的点集。这并不意味着不能有一个,只是统计上不太可能。一些代数揭示了当 k 超过 π 除以3的平方根时,这个系数为负。

所以,这个猜测是这是一个限制。对于一个 n x n 的网格,你不太可能能够放置比 n 乘以 π 除以3的平方根多的点而没有其中的三点共线。

结论
我们从一个关于国际象棋棋盘的有趣的小谜题开始,一直到人类知识的边缘——数学家只做了有根据的猜猜。希望你能看到,为什么在追求答案的过程中,每一步都是合理的。像这样的开放数学问题随处可见,只要你深入挖掘,就会发现,正如旧的问题得到了答案,新的问题也被提出。所以,快点出去探索吧!
