傅立叶变换，这个被广泛应用于科学、工程和数学的强大工具，通常被理解为一种从时域到频域的转换机制。但要真正掌握它，我们需要进一步剖析其背后的数学原理。

令f为一个由R到R的函数。在典型情况下对于f并没有什么可说的，但是有些函数具有有用的对称性质。例如，若对于每一个x都有f(-x)=f(x)，就说f是一个偶函数，而若对每一个x有f(-x)=-f(x)，就说f是一个奇函数。进一步说，每一个函数都可以写成一个偶函数f_e（称为f的偶部）和一个奇函数f_o（称为f的奇部）的叠加。例如，函数

既不是偶的，也不是奇的，但是，它可以写成

其中

对于一般的函数f，这种分解是唯一的，而由公式

和

给出。

偶函数和奇函数有什么样的对称性呢？下面是一个对待它们的有用的方法。有一个由实数轴上的两个变换构成的群：一个变换是恒等变换：

另一个是反射：

实轴上的任意变换Φ都会诱导出定义在实轴上的函数的变换如下：给定一个定义在实轴上的函数f，变换后的函数就是g(x)=f(Φ(z))。对于当前的情况，若

则变换后的函数是就是f(x)本身，而若Φ=p，则得到f(-x)。若f是偶函数或奇函数，则变换后的函数是原来函数f的标量倍数。特别是若Φ=p，则当f为偶函数时，变换后的函数仍为f(x)，而作为倍数的标量是1；当f为奇函数时，则变换后的函数是-f(x)而这个标量是-1。

上面描述的过程可以看作是傅里叶变换的一般概念的很简单的原型。非常广泛地讲，一个傅里叶变换就是一种把非常“一般”的函数分解为“对称”函数的叠加的系统方法。这些对称的函数通常都是显式定义的，例如，最重要的就是分解为三角函数 sin(nx)和cos(nx) 的线性组合，它们也时常与频率和能量这些物理概念相关。对称性一般是与一个群G相联系的，这个群又通常是阿贝尔群（在上面的例子中，它是一个含两个元素的群）。

阿贝尔群的特点在于，它满足交换律，也就是说，无论怎样调换元素的运算顺序，运算结果都是相同的。

说真的，傅里叶变换是研究群的理论，准确一些说是研究群表示理论的基本工具，这个理论关注的就是一个群可以怎样在不同方式下看成是对称群。傅里叶变换也与线性代数的一些主题有关，例如，向量之表示为规范正交基底的线性组合，或者表示为一个矩阵或线性算子的本征向量的线性组合。

现在来看一个比较复杂的例子。固定一个正整数n，我们要给出一个把由C到C的函数，即复平面上的复函数加以分解的系统方法。若f是这样一个函数，而j是介于0到n-1间的整数，我们说f是一个j阶谐振子，如果它有以下的性质：

即若ω是1的一个n阶本原单位根：

这时，对于任意的复数z∈C，有

注意，若n=2，则ω=-1，所以若j=0就会回到偶函数的定义，而若j=1，就回到奇函数的定义。事实上，受到这件事的启发，就会得到把f分解为谐振子的一般公式，而这种展开也是唯一的。其作法如下：若定义

则证明对于任意复数z∈C有

只是一个简单的习题，而且还有

这样，f可以分解为谐振子之和。这就是一个傅里叶变换，而与它相联系的群就是n阶单位原根：

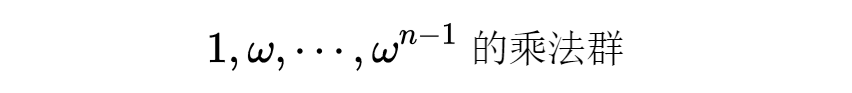
即n阶循环群。

现在考虑无限群。令f为定义在单位圆周T上的一个复函数。为了避免一些技术上的问题，假设f为光滑的，即无限可微的。如果f是一个形状简单的函数

n是一个整数，而c是一个常数，则f有n阶的旋转对称性。即是说，若再令

则对于任意复数z∈C，f(ωz)=f(z)。从前面的例子看到，并不惊奇，任意光滑函数f都可以表示为这种旋转对称函数的叠加。事实上，有

数

称为f在频率为n处的傅里叶系数，而由下式给出：

这个公式可以看作是上面fj(z)的公式，当z限制在单位圆周上且n趋于无穷时的极限。它也可以看作是全纯函数的泰勒级数的推广：若f在闭单位圆盘上是全纯的，则有

而泰勒系数an由下式给出

一般说来，傅里叶分析与复分析有很紧密的联系。

全纯函数（又称解析函数或正规函数）是复分析中的基本概念。它是在复数域上定义并满足某些特性的函数。

给定复变量 z，如果函数 f(z) 在其定义域内的每一点都存在复导数，那么这个函数就称为全纯函数。简单地说，全纯函数就是在其定义域内处处可微的复函数。

如果f是光滑的，则其傅里叶系数衰减于0非常快，而很容易证明其傅里叶级数

但是，如果f不是光滑的（例如只是连续的），问题就微妙多了，这时必须仔细确定这个级数收敛的确切的意义。实际上调和分析的相当一部分就是在讨论这一类问题，以及解决这类问题所需的工具。

与傅里叶分析的这种讲法相关的群是圆周的群T。注意，我们既把数

看成圆周上的一点，又把它看成旋转一个角θ。这样，这个圆周和它的旋转对称群可以等同起来。但是还有第二个群在这里也很重要，即所有整数所成的加法群Z。如果取两个基本的对称函数z^m和z^n并把它们乘起来，就会得到z^（m+n），所以映射

就是由Z到这些函数在乘法下所成的群的同构。群Z就称为T的庞特里亚金对偶。

在偏微分方程以及调和分析的相关领域里，最重要的傅里叶变换是定义在欧几里得空间R^d上的。在所有的函数

取平面波：

为“基本的”函数，这里ξ∈R^d是一个向量（称为平面波的频率），x·ξ是位置向量x和频率向量ξ的数量积，

注意，形如

是正交于向量ξ的（超）平面，在每一个这样的集合上，平面波f(x)取常数值，而f在H_λ上的值与在H_λ+2π上的值相同。平面波一词即由此而来。可以证明，若f相当“好”(例如是光滑的，而且当x变大时衰减到0相当快)，它就可以唯一地表示为平面波的叠加，不过这里的“叠加”要用一个积分而不是求和来表示。更确切地说，有

其中

而前一个公式则称为逆傅里叶变换公式。这两个公式告诉我们怎样从原来的函数求出其傅里叶变换，以及相反。我们可以把

可以证明，当f相当“好”的时候，论证这些积分的收敛性毫无困难，然而当f比较粗糙或者衰减得不太快的时候，这些问题又变得很微妙，在R^d上的傅里叶变换的情况下，相关的群是欧几里得群R^d

还要注意，现在位置x和频率ξ都含于R^d内，所以R^d在这个背景下，正是自己的庞特里亚金对偶。

傅里叶变换的一大用途是用它来理解作用在函数上的各种算子，例如，R^d上的拉普拉斯算子，给定一个函数f:R^d→C，拉普拉斯算子△f的定义是

这里把向量x写成分量形式，而把f看成d个实变量的函数：

为了避免技术细节，只考虑那些足够光滑使得上式有意义而不产生困难的情况。一般说来，一个函数f和它的拉普拉斯算子△f之间并无明显的关系。但是，若f是平面波

则二者有明显的关系：

就是说拉普拉斯算子作用在平面波上的效果就是把它乘以标量：

换句话说，

（一般说来，平面波将是任意与平行移动可交换的线性算子的本征函数）。所以，透过傅里叶变换的棱镜来看拉普拉斯算子是很简单的：傅里叶变换使我们能把任意的函数写成平面波的叠加，而拉普拉斯算子在每一个平面波上的效果又很简单，讲清楚一点，就是

此式给出了拉普拉斯算子作用在一般函数上的公式。在这里交换了拉普拉斯算子与积分的次序，对于适当好的函数，这是可以严格论证的，但是我们略去细节。

这个公式把△f表示为平面波的叠加。此外，逆傅里叶变换的公式又告诉我们

但是，一个函数表示为平面波的叠加的方法是唯一的，所以

这一个事实当然也可以由傅里叶变换的定义直接导出，这个恒等式说明，傅里叶变换把拉普拉斯算子对角化，就是说，从傅里叶变换看来，对某个函数施加拉普拉斯算子，无非就是把这个函数的傅里叶变换F(ξ)乘以乘子

换言之，拉普拉斯算子可以看成一个傅里叶乘子。这句话的意思是，如果想要计算拉普拉斯算子对于一个函数的作用，可以先取这个函数的傅里叶变换，乘上乘子，再取逆傅里叶变换。这个观点使得拉普拉斯算子的操作变得很容易。例如，可以迭次使用这个公式来计算拉普拉斯算子的各次幂：

事实上，现在已经可以定义拉普拉斯算子的更加一般的函数。例如，可以取拉普拉斯算子的平方根如下：

这就会引导到分数阶微分算子理论，还有更一般的函数演算理论，在其中，我们从某一个算子（如拉普拉斯算子）开始，然后研究这个算子的各种函数，例如平方根、指数、倒数，等等。

正如上面的讨论所表明的那样，傅里叶变换可以用来发展许多有趣的运算，而这对于微分方程理论有特别的重要性。为了有效地分析这些运算，需要傅里叶变换的种种估计。例如，了解一个函数f的用某种范数表示的大小，与其傅立叶变换的可能用其他范数来表示的大小的关系，这时常是重要的。关于这一点的进一步讨论可见条目函数空间。这种类型的估计中特别重要而又惊人的是普兰舍利公式

它表明，一个函数的傅里叶变换的L₂范数与原来函数的L₂范数恰好相等。所以，傅里叶变换是一个酉变换，因此可以把一个函数的频率空间表示看成是它的物理空间表示的某种意义的旋转。

在线性代数中，一个酉变换（Unitary Transformation）是一个保持向量内积不变的线性变换，也就是说，如果你有两个向量，在变换前后，它们的内积保持不变。

发展与傅里叶变换以及相关算子的进一步的估计是调和分析的很大一个部分。普兰舍利恒等式的一个变体的傅里叶变换的卷积公式

这个公式使我们能用两个函数f和g的傅里叶变换来分析它们的卷积

特别是，若f或g的傅里叶变换很小，则我们可以期望它们的卷积f*g也很小。这个关系意味着傅里叶变换控制了一个函数和它自己以及和其他函数的某些相关性，这就使得傅里叶变换成了研究随机性以及概率理论、调和分析和数论中的其他对象的均匀分布性质的重要工具。例如，我们可以追随这个思想来确立中心极限定理，这个定理表明许多独立随机变量的和最终会像是一个高斯分布；我们甚至可以用这个方法来证明维诺格拉多夫定：任意充分大的奇数都是三个素数之和。

以上这些思想可以在多个方向上推广。例如，可以用比较一般的算子代替拉普拉斯算子，用这个算子的（广义）本征函数代替平面波，这样就得到谱的理论和函数演算。也能抽象地研究傅里叶乘子的代数，这就引导到C'-代数。还可以越出线性算子理论来研究双线性、多线性甚至完全非线性算子，这特别会引导到仿积的理论。仿积是点态乘积运算(f(x)，g(x))→fg(x)的推广，它在微分方程中有重要性。

在另一个方向上，也能用更一般的群来代替R^d，这时，平面波的概念就会被群特征标概念（在阿贝尔群的情况）取代，或者被群的表示（在非阿贝尔群的情况）所取代。傅里叶变换还有其他变体，如拉普拉斯变换、梅林变换，它们在代数上很像傅里叶变换，而且作用也相似（例如，拉普拉斯变换在微分方程上所起的作用）。我们已经看到傅里叶变换与泰勒级数有关，它还与其他重要的级数展开式有联系，需要提到的有狄利克雷级数，以及函数按特殊多项式的级数展开，例如，按正交多项式或球面调和的展开式。

傅里叶变换是把函数分成许多成分，而每一个成分恰好有一个准确的频率。但在有些应用中，采取一种比较“模糊”的途径更为有用。这时，函数被分解成的成分数目要少一些，但是每一个成分所含的频率构成一个频段，而不是单个频率。这样一种分解有一个优势，就是受到不确定性原理的限制较少，因为按照不确定性原理，一个函数及其傅里叶变换不可能同时局限在R4的很小的区域里。这样会导致傅里叶变换的某些变体，如小波变换，它对许多应用数学和计算数学问题更为适合，也对某些调和分析和微分方程的问题更为适合。对于量子力学起基本作用的不确定性原理也把傅里叶变换与数学物理联系起来，特别是经典物理和量子物理的联系，可以通过几何量子化和微局部分析的方法作严格的研究。