
几何学的最基本的图形之一是环面,这是一个轮胎形的曲面。如果想要作一个环面,可以取一个正方形,并且先把它的一对对边,例如,上下对边粘起来,这样就得到了一个柱面,然后再把它的另外一对对边(即原来正方形的左右对边)粘起来,就得到了环面。

下面是环面的更加数学化的作法。我们从通常的(x,y)坐标平面开始,在其中作以四点(0,0),(1,0),(1,1),(0,1)为顶点的正方形,它是由坐标适合0≤x≤1,0≤y≤1的点构成的。可以在水平和铅直两个方向上移动这个正方形。如果在水平方向移动m个单位,在铅直方向上移动n个单位,这里m和n是整数,就会得到由坐标适合下面的不等式的点所成的正方形:m≤x≤m+1,n≤y≤n+1。当m和n遍取一切整数值时,这个正方形的复本就构成整个平面的一个铺砖结构(tessellation,或者说平面被铺上了砖),而在每一个坐标为整数的点,有4个正方形相会。如果把这些小正方形黑白相间地图上颜色,就会得到一个无限大的国际象棋棋盘。

要做一个环面,就需要把某些不同的点等同起来。我们说点(x,y)和(x',y')相应于某个新图形上的同一点,如果x-x',y-y'都是整数。要想看一下这个新图形究竟是什么样,就要注意,平面上的每个点都相应于原来的正方形的一个内点或边界上的点。此外,如果x和y都不是整数,则(x,y)相应于正方形的恰好一个内点。所以新图形看起来很像原来的正方形,但是(1/4,0)和(1/4,1)这两个点又如何?它们相应于新图形的同一点,原来的正方形的上下对边的相应点也都相应于新图形的同一点。所以,在新图形中,要把原来正方形的上下两边等同起来。用类似的论证知道左右两对边也要等同起来。因此当把各个点按上述规则等同以后,就得到了环面。
如果这样作出了环面,就可以这样来在环面上作图:只要在原来的正方形上作图,再把相应点等同起来就行了;正方形上的长度与环面上的长度相应,而且准确地相等。老式的滚筒印刷机就是这样工作的:滚筒上涂了油墨的图形滚过纸张,就印出了完全一样的图形。
这样,就小图形而言,环面上的几何学就是欧几里得几何学。用数学语言就说,环面上的几何学是由平面上的几何学诱导而来,所以环面是局部欧几里得的。当然,整体而言二者很不相同,例如在环面上,可以作出不能收缩为一点的封闭曲线,而在平面上就不会有这种事情。
还要注意,我们引进了一个群来为我们完成了大部分工作。在现在的情况,这个群就是整数对(m,n)所成的群,而定义

环面和球面只不过是无穷多种以下的曲面中的两个例子,这些曲面是封闭的(就是说,没有边缘),又是紧的(就是说它们在任何意义下也不会走向无穷)。其他的例子则有:两个孔的环面,以及更一般的具有n个孔的环面(即亏格为2,3,4,…的曲面)。要想类似地生成这些曲面,就要用到富克斯群(Fuchsian Groups)。
在数学中,特别是在复分析和代数几何中,"亏格"(genus)是一个用于描述曲面拓扑类型的重要参数。对于紧致的,连通的,定向的二维实曲面(或者等价的,复一维的Riemann曲面),它的亏格定义为它的"手柄"的个数。形象地说,亏格为0的曲面类似于球面,亏格为1的曲面类似于甜甜圈(或称之为圆环面),亏格为2的曲面类似于有两个洞的甜甜圈,等等。
亏格是一个拓扑不变量,也就是说,如果两个曲面可以通过连续的弯曲和拉伸,而无需撕裂或者粘贴,从一个变为另一个,那么这两个曲面的亏格就是相同的。
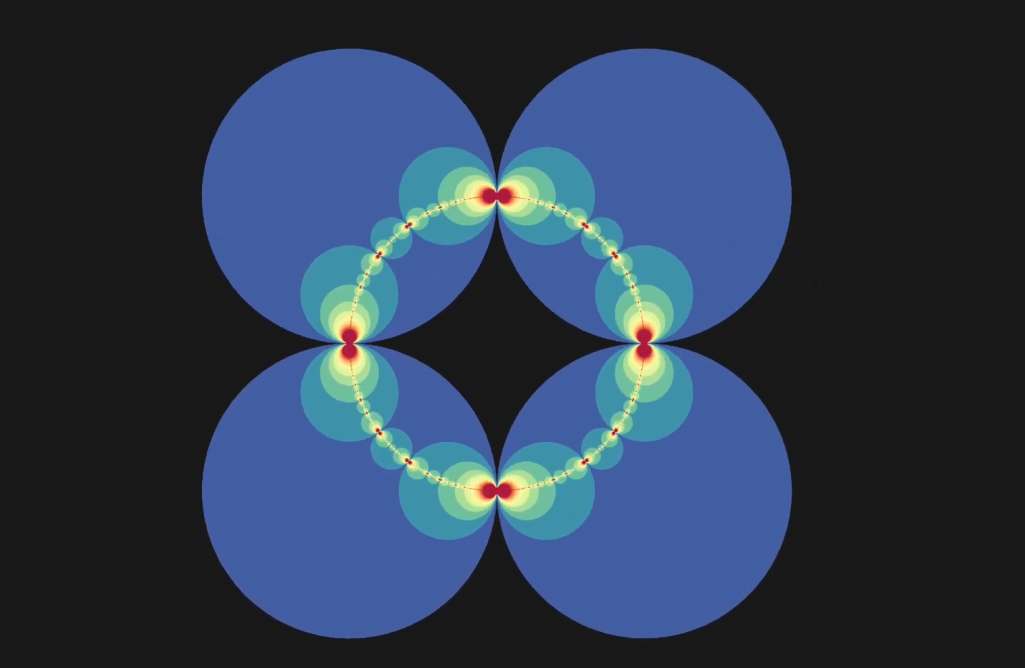
我们自然会期望,利用多于4边的多边形就能得出其他曲面。结果是,如果利用8边形,例如正8边形,并把边1和3粘在一起,2和4粘在一起,5和7粘在一起,6和8粘在一起,就会得到一个具有两个孔的环面。我们怎样用群来做这件事,就如刚才对于环面所做的那样?为此我们需要有一种方法,把许多8边形连到一起,使得它们只在边上相接。问题在于我们不能用8边形来作出平面的铺砖结构:正8边形的顶角为135°。这个角太大了,不可能把8个正8边形在一点粘到一起。
这里前进的道路是采用双曲几何学来代替欧几里得几何学。但是,我们可以徒手来做这件事。在复平面上取单位圆盘
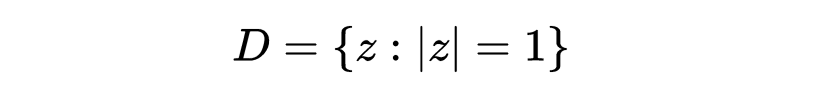
取所谓莫比乌斯变换的群,而莫比乌斯变换,就是形如

的映射,经过常规的计算就知道,这些变化把圆周和直线映为圆周和直线(这两种曲线要视为同一种,所以圆周也可以被映为直线,或者相反),它们把角映为大小相等,而且方向也相同的角。还有一些变换是把角映为大小相等但符号相反的角,好像平面上的反射那样,如果取把D映为自身的莫比乌斯变换,就得到一个群,记为G。事实上,我们已经很接近于富克斯群了。
我们要找一个图形,使它在这里起到正方形在欧几里得平面上所起的作用。正如我们在上面把圆周和直线视为相同曲线一样,现在视D的直径和垂直于D的边缘的圆弧为相同的曲线,则G中的元素映垂直于D的边缘的圆弧(包括直径)为垂直于D的边缘的圆弧(包括直径)。
我们以后就以垂直于D的边缘的圆弧(包括直径)为直线,其实是非欧几里得的直线,并以8条这样的非欧几里得直线为边作出(非欧几里得)八边形。这种八边形的作法有许多,我们要选择最具对称性的一种,使得以后事情更加容易。即要画一个以D的中心为心的“正八边形”。这里还有进一步选择的余地,因为按照双曲几何学中多边形的角的亏值正比于其面积的著名定理,八边形面积越大,其顶角就越小,我们要画的是顶角为π/4的正八边形,这样一来就可以让8个这样的正八边形汇聚在一个顶点处,这就是我们需要的正八边形。如果我们把不同的多边形在不同位置的相应的点等同起来,所得的图形就是一个亏格为2的黎曼曲面。
黎曼曲面(Riemann Surface)是复分析和微分几何中的一个基本概念。它是一种特殊的二维复流形,可以被看作是一系列复平面(或者称为“图表”)按照某种规则拼接而成的空间。
富克斯群就是群G(即变D为其自身的莫比乌斯变换所成的群)的这样的元所成的子群。这些元能把上面得到的正八边形“整块地”移动,使得我们就能做出D的一个铺砖结构。和在环面的情况一样,现在也有了等价点(即在不同“砖块”中占有相应位置上的点)的概念,当把等价的点等同起来以后,就会得到最前面说的把多边形的不同的边粘连起来得到的图形。这就是我们需要的图形。
所有这些都可以用双曲几何学的语言来描述。我们得到的将是双曲几何学的圆盘模型,它也可以用D上的一种黎曼度量来定义,这个度量就是

G的元素将把图形在D中移来移去,但保持双曲距离不变。由此可知,在新的曲面(即把不同的对应点等同起来得到的图形)上得到的几何学是局部双曲的几何学,正如在环面上得到的几何学是局部欧几里得几何学一样。
因此,如果从正4n(n>2)边形开始,并按上面的方法进行,就会得到亏格为n的黎曼曲面,但是数学家们能做的事情还更多,如果回到平面,但是不从正方形开始,而从矩形开始,或者更加一般地从平行四边形开始,想要看出上面的做法可以继续实行下去,这不算太难。事实上,如果从一个适当的角度来看平面,而不是从平面的铅直上方来看这个平面,则正方形也就会变成任意选择的平行四边形(可能会放大或缩小一点)。
如果用的是平行四边形,仍然会得到一个环面,不过与最早得到的环面不同,其区别正如正方形和平行四边形的区别一样:顶角的大小发生了变化。下面是一个不算是完全平凡不足道的习题:证明平行四边形的保持顶角大小不变的映射只能是相似变换(就是在两个独立的方向上缩放的比例相同,从而在一切方向上缩放比例相同的变换)。所以得出的环面在什么角度上有不同的意义,就是说,这样得出的环面与原来的环面有不同的共形结构。
在双曲圆盘上也会发生同样的事。如果取一个4n边多边形(它的边是一段测地线),而且其边长成对地相等,并能找到一个群,其元素能把这些多边形成块地移动,使得适当的边准确地相配,则又会得到一个黎曼曲面。但是,若这些多边形不是共形等价的,则所得黎曼曲面也会有不同的共形结构。甚至还可以向前再走一步,允许某些顶点位于圆盘的边缘上,这时,多边形的相应的边的长度在双曲度量下将会是无穷大。这样得到的图形是“挖掉一点”的黎曼曲面,而数学家们又可以改变它的共形结构。
富克斯群的基本重要性来自单值化定理,这个定理指出,除了最简单的以外,所有的黎曼曲面都是按照上述方式来自某个富克斯群,这里面包括了所有亏格大于1的黎曼曲面和所有亏格为1但挖掉了一点的黎曼曲面,并允许它们具有任意可能的共形结构。
富克斯群这个名词是庞加菜在1881年给出的,那时,他正在研究超几何方程和相关的微分方程,而这是受到了德国数学家富克斯(Immanuel Lazarus Fuchs)的工作的启发。克莱因提出了抗议,认为以施瓦兹命名更好,庞加莱在读了施瓦兹相关的文章以后,本来也准备同意这样做,但是那时,富克斯也已经赞成用这个名字。但是克莱因的抗议有点过分,于是庞加莱又把研究3维单位球体的共形映射所产生的一个类似的群公开称为克莱因群。这些名字一直沿用至今。但是克莱因群的研究要困难得多,而克莱因和庞加莱对此都没有能做多少事情。但是每一个黎曼曲面都来自球面或者欧几里得平面或者双曲平面,这是他们二人都具有的猜测。但是严格的证明,直到1907年才由庞加莱和寇贝独立地给出。
富克斯群的形式定义如下:所有莫比乌斯变换所成的群的一个子群H称为不连续作用的,如果对于圆盘D的每一个紧集合K,h(K)和K都是互相分离的,除了对于有限多个h∈H例外。富克斯群就是所有的不连续作用于D的莫比乌斯变换所成的群。

好文章
能聊聊自守函数码?