狄拉克δ函数，这是一个看似简单，但却充满深度和意义的数学工具，常常在物理学和工程学的许多领域中出现。虽然在一般的意义下，它并不是一个函数，但其独特的性质使得我们能够用它来描述和处理无穷小和无穷大的现象。狄拉克δ函数的美在于其优雅的定义和强大的应用：虽然它在每个点上几乎都为零（除了在原点），但是它的整体积分却等于一。这使得δ函数成为了描述和处理脉冲和点源等现象的理想工具。

让我们考虑一个电荷"Q"，它均匀地分布在一条薄线上。我们可以用一维电荷密度"rho"来描述这种分散的电荷。由于它是一维的，因此只依赖于一个空间坐标"x"。

一维电荷密度是每单位长度的电荷。也就是说：如果在电荷分散的线上积分电荷密度，可以计算出电荷 Q，

但是，如果没有一个分散的电荷 Q，而是一个集中在一个点的电荷呢？假设Q位于原点，即"x 等于零"的位置。电荷密度必须具有哪些性质才能描述一个点电荷呢？

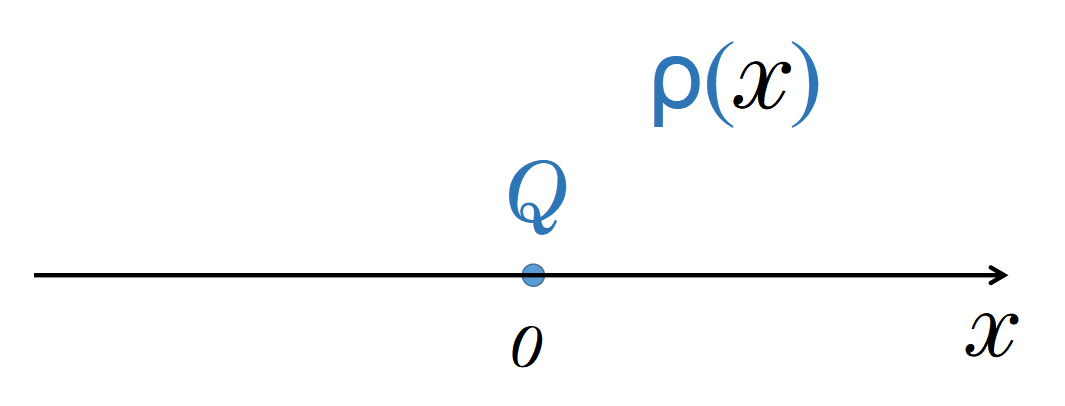
如果电荷密度描述的是一个单点电荷，它必须满足两个属性。

它在每个位置 x 都必须为零，除了点电荷所在的位置，即x 等于0的位置。

如果在点电荷所在的两点“a”和“b”之间对电荷密度进行线积分，那么线积分必须得到点电荷 Q 的值。

另一方面，如果对电荷 Q 不在的区域进行积分，那么积分应该为零。

让我们总是包含电荷 Q，因此，选择积分限为负无穷大到正无穷大。如果将电荷标准化到 Q = 1，并考虑到上面的两个属性，那么我们用一个希腊字母delta δ来表示这个电荷密度，并称之为狄拉克的δ函数（Dirac's Delta Function）。

虽然名字可能暗示，但delta函数在数学上不是一个函数，而是另一个数学对象，可以理解为所谓的分布或狄拉克测度（distribution or Dirac measure）。这我们并不关心数学上的清晰定义。只想知道如何使用 delta 函数。

δ函数图形

δ函数用位于点电荷位置的箭头来表示。箭头的高度通常被选为代表积分的值，在这种情况下是1。

原点的δ函数的积分

现在让我们考虑δ函数和另一个行为良好的函数 f(x) 的积分。

这样的积分非常容易计算，因为δ函数在"x = 0"的点之外的所有地方都是零。因此，乘积在"x =0"的点之外的所有地方也都是零。只剩下函数值 f(0)。由于f(0)不再依赖于x，我们可以将它放在积分的前面，

δ函数的积分是1，所以我们知道δ函数在积分中与函数 f(x) 相乘时的作用，它选择在位置 x=0的函数值，

位移后的δ函数

我们当然可以将电荷移动到x轴上的另一个位置，例如到正位置 x0。那么Delta函数必须在新位置以外的所有地方都是零。我们将Delta的参数改为"x-x0"。

“减去x0"是因为我们将Delta 函数向正方向移动。δ函数的积分是1。我们只是将δ函数移动到 x0，因此积分的结果与δ（x）的结果相同，

位移后的δ函数的积分

如果在积分中出现了另一个函数 f(x) 和位移后的δ函数，那该怎么办？

Delta在x0的点以外的所有地方都是零。为了图解说明：在积分中，位移后的δ选择在δ函数当前位置的f的函数值。

你可以通过将"x-x0"替换为y来证明这一点。δ函数中的"x-x0"变为 "y"。

函数中的"x"变为 "y 加上 x0"。

对 y 关于 x 的导数为1。因此 "dx"变为 "dy"。

我们知道，δ(y)在积分中选择在"y =0"的点的函数值。因此，积分得到"f(x0)"的值。

δ函数是对称的（偶函数）

接下来，让我们看看当δ中有"-x"时会怎样。

做一个替换"y 等于-x"。

y关于x的导数是“-1” ，

因此用“-1dy"替换 "dx"，下限变为正无穷，上限变为负无穷。

为了使积分再次从负到正，我们反转积分限，

因此在积分前面得到一个负号。我们已经知道δ(y) 在积分中的作用：它选择在"y等于0"的点的 f 的值。所以这个积分得到f(x)的值。

但我们也知道，没有负号的δ函数的积分也得到f(0)。

所以在积分中使用δ(x) 或δ(-x)没有区别，δ函数是对称的。

δ函数的因子

如果我们通过一个因子k来缩放δ中的x，会发生什么？

如果k是负的，由于对称性，可以直接把负号去掉。做一个替换，

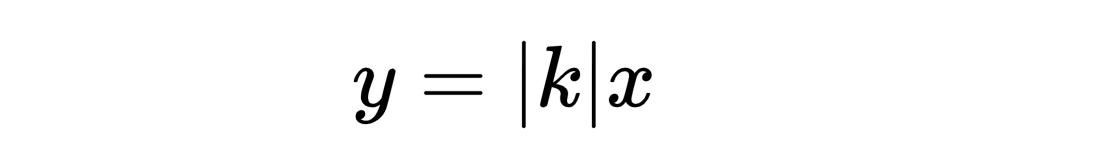
y"关于x的导数是|k|，因此

把dx替换掉得，

如你所知，这个积分在点"y=0"处选取f的值，因此我们得到

这里必须注意，k不能为零。

例子

让我们通过几个例子，看看这个函数在函数的积分中的作用。

这个积分的结果是f(0) ，

将x=0代入。0的正弦是0。e的0次方是1。所以积分等于-2。这就是当积分中出现Delta函数时，如何轻松计算复杂积分的方法。

再看一个例子：

这次的积分并不是从"负无穷大"到"正无穷大"，而是从-1到1。因此我们首先要确保δ函数在积分限内。δ函数在这里被偏移到了"x=3"的位置，并且在上面的积分限之外。

因此，积分等于零。

最后一个例子：

δ函数在"x=-π"的位置，并且在积分限内。

所以我们必须在"-π"的位置计算余弦，得出积分的值是：

三维的δ函数

到目前为止，我们只考虑了一维的δ函数。电荷通常位于三维空间中。

如果单位点电荷位于原点，那么我们可以用三个δ函数的乘积来描述其电荷密度：

只有当电荷位于原点(0, 0, 0)时，这个乘积才非零。如果我们将电荷移到正方向的位置(x0, y0, z0) ，

那么我们必须像在一维情况下那样调整δ函数的参数。为了不必写三个δ，我们将它们合并为一个δ，并在上面写上3，在参数中我们写位置向量"r"，位移为r0。

一维情况下的线积分变成了三维情况下的体积积分，并且如果我们在包含三维δ函数位置的体积V上进行积分，那么结果为1。