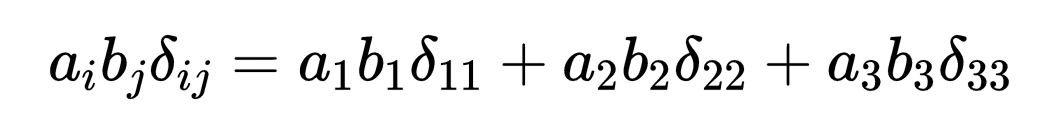克罗内克Delta函数,虽简单却影响深远,它为许多数学和物理领域的研究提供了基础。这个函数以德国数学家利奥波德·克罗内克的名字命名,以其独特的特性在诸多数学理论和公式中发挥着重要作用。
在理论物理中,我们几乎无法想象没有克罗内克δ(Kronecker delta)的情况,它的形式如下,

这个相对简单但功能强大的张量(tensor)在理论物理的所有领域都有应用。例如,它被用于将长表达式写得更紧凑,以及简化复杂的表达式。与莱维-奇维塔张量(Levi-Civita tensor)结合使用时,这两个张量非常有用!

δ_ij 取值为1或0,具体取值取决于其两个下标 i 和 j 的值。下标的最大值对应于考虑的维数,所以在三维空间中,i 和 j 的范围是1到3。当 i 和 j 相等时,δ_ij等于1。当 i 和 j 不等时,δ_ij 等于0,

让我们看一些例子,

因为下标相等。

因为下标不相等。


爱因斯坦求和约定(Einstein's Summation convention)
为了紧凑地表示像这样:

或像这样的表达式:

我们约定如下的求和规则:省略求和符号,

但要记住,如果在表达式中出现两个相同的下标,那么就对该下标求和。

求和约定的另一个优点(除了紧凑性)是形式上的可交换性。例如,你可以按照你希望的顺序写下表达式,例如这样:

这可能帮助你看到什么可以进一步缩减或简化。
但有些例外,例如与微分运算符

partial_j,作用于一个后继项。你不能将被求导的项移动到微分前面

所以在使用下标表示法时,应该小心处理运算符。
现在让我们学习一些使用克罗内克函数的重要规则。
性质1:克罗内克函数是对称的,

为什么?根据定义,如果下标i和j相等,那么δ_ij 等于1,那么δ_ji也等于1。如果下标不等,δ_ij=0,δ_ji也等于0。所以,克罗内克函数是对称的!
性质2:下标缩减

如果两个或更多的克罗内克函数的乘积包含一个求和下标,那么乘积可以缩减,使得求和下标 j 消失。
为什么?让我们考虑例如当下标 i 和 j 相等的情况:i = j,而下标 j 和 k 不等:j ≠ k ,那么就得出 i 和 k 也必须不等:i ≠ k。所以δ_jk 是0,因此左手边的整个项是0:

而左手边的δ_ik 也是0,因为i和k是不同的,所以等式成立。
让我们通过一些例子来更好地理解,

下一个例子:

性质 3:下标转移

如果在 a_j 中的下标也出现在克罗内克函数 δ _jk 中,那么δ 消失,而因子 a_j 获取另一个下标 k。
这个规则基本上是下标缩减的另一种情况。这个规则告诉你,你也可以缩减不需要由克罗内克尔δ携带的求和下标。让我们再举一个例子,

性质 4:相等下标求和
如果 j 从1运行到 n,那么:

为什么这样?根据求和约定:在这里,求和是通过 j 进行的。所以

每个 δ 都是1,因为下标值是相等的。
δ 的标量积
现在我们来写出带有克罗内克δ的标量积。考虑一个由x,y,z三个部分组成的三维向量v = (x, y, z):

你可以按照下述方法在标准正交基下表示此向量:

这里x,y和z是彼此正交并被规范化的三个基向量。在这个例子中,他们构成一个正交的三维坐标系统。
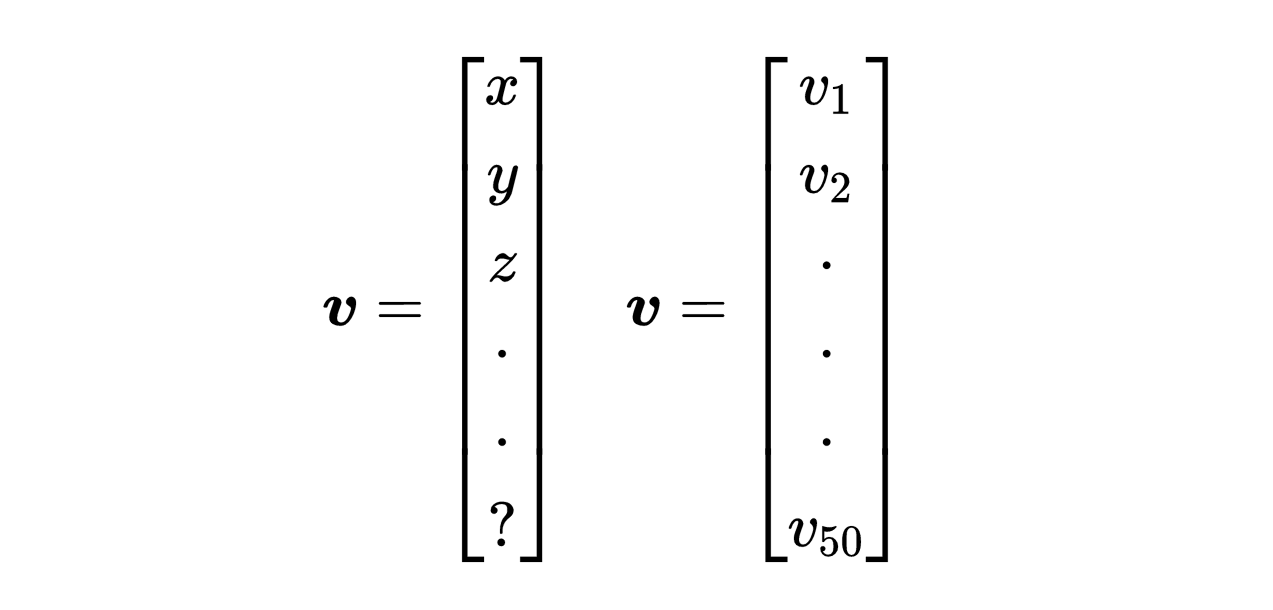
δ要用索引记号写出向量。这里我们不用不同的字母x,y,z来表示向量的分量,而是选择一个字母(在这里是字母v)然后连续对向量的分量和基向量进行编号。然后,向量的分量被称为v_1,v_2,v_3,并且基展开如下所示:

这种索引记号的优点在于,这样你永远不会用完向量分量的数字。试想一下一个五十维的向量,没有足够的字母给向量的每一个分量v_1,v_2直到v_50一个独特的字母。
另一个索引记号的优点在于,通过这种方式对向量分量进行编号,可以用求和符号更紧凑地表示基的展开,

如果省略求和符号,它就变得更紧凑,

在这里,我们对索引j进行求和。
现在我们知道了一个向量如何在指标记号中表示,我们可以类比地写出两个向量a和b的标量积,

使用刚刚学习的向量的索引表示:

在索引记号中,你可以按你喜欢的方式排序因子。这就是索引记号的优点,其中交换律适用。利用这个,把括号放在基向量周围,以强调引入克罗内克δ的重要性:

基向量e_i和e_j是正交规范的。回忆一下对于两个向量来说,成为正交规范化的属性意味着什么?他们的标量积的要么是1,要么是0:

两个正交规范化向量的标量积正好像克罗内克函数,

因此,用δ替换两个基向量的标量积:


根据第三条性质,可以缩减求和索引j,

然后就得到了标量积的精确定义,

为了练习,我们可以写出对i和j的求和,列出所有可能的i和j的组合:

如你所见,由于克罗内克函数的定义,共9个分量中只有3个不为零,即i = j;省略所有不相等的索引的求和项(0);并且,使用克罗内克δ的定义有:

这就得到了我们熟悉的标量积: