黎曼猜想可能是有史以来最大的未解数学问题，但它只是一个更大故事的一小部分，这个故事就是寻找支撑L函数理论的新几何的探索。

在黎曼猜想的传奇世界里，我们将解释L函数是什么，阐述这个新几何的梦想，有些人称之为一元域上的几何（geometry over the field with one element），或F1。我会解释它与黎曼猜想的联系，以及其他伟大的问题，比如BSD猜想和朗兰兹计划（langlands program）。这是一段漫长的旅程，起点是L函数的理论，其中最简单的例子就是黎曼ζ函数。梦想是找到这个未知的、隐藏的、难以捉摸的F1几何。我们的希望，就是这个几何能为黎曼猜想的证明开启一条路径。

首先，我想向你们展示马宁（Manin）的一篇文章，作为F1的入门，然后简要回顾一下黎曼猜想，最后说一些关于如何寻找黎曼猜想证明的事情。

作为对F1的初次接触，我向你们展示尤里·马宁的一篇文章。马宁是一个传奇人物，他是世界上为数不多的拥有全面数学知识的数学家之一。在这篇文章中，我只想指出一些我们将来会遇到的关键想法。你们可以自己阅读这篇文章，它是公开可见的。

文章的标题是“把数字看作函数（NUMBERS AS FUNCTIONS）”，其思想是为了解决数论中最深奥的问题，我们可能需要重新想象数学的核心本质。特别是，我们可能需要重新思考我们对“数字”这个词的理解。马宁讨论了一种特定的做法，这是按照亚历山德鲁·布伊乌姆（Alexandru Buium）的理论发展出来的。在摘要中，你可以看到这个短语，“一元域上的几何”。

他还提到一个非常意外的想法，即素数和物理之间可能存在深层的联系。整篇文章都是在讲述一个故事，即许多不同的想法之间存在意想不到的联系。让我们一起浏览这篇文章。

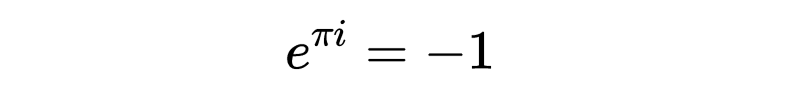
首先，这可能是最著名的数学公式之一，e 的 πi 次幂等于负一。他还提到了黎曼ζ函数的特殊值，即 π^2/6，

你可能在与巴塞尔问题的关系中看到过这个公式。文章开头的讨论主要关注一类特殊的数字，它们在量子场论中出现的原因令人费解。这些数字被称为周期（periods）。

在第三页，我们遇到了一个超级重要的想法，即单位根（roots of unity）。

然后在第四页的开头，他提到了我们的希望，即接近黎曼猜想。

一些有趣的周期示例包括代数数字，也就是多项式方程的零点，数字π也是一个周期，然后还有这些奇怪的数字，

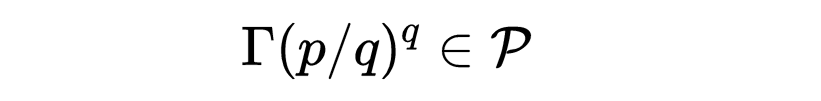
这可以通过将伽马函数应用于有理数来得到。所以我们可以把它们叫做分数伽马值（fractional gamma values）。

这里的所有内容都非常有趣，我想提到的最后几个概念是费曼积分或费曼路径积分（Feynman path integrals），它们与量子场论中的振幅有关。然后在第14页，有些概念被称为格罗滕迪克环和维特环（Grothendieck rings and Witt rings）。

它们是具有所谓"lambda-运算”的代数结构的例子。

在第16页，我们看到了一个被称为F_q的东西，这是一个有限域，我们会回过头来再谈这个，还有这个符号F_1，它是这种神秘几何的核心。

最后在第18页，他使用了“深不可测的深渊”这个短语，我非常喜欢这个词，因为它传达出在这个思想空间中你遇到的深度的感觉。

我们快速回顾一下黎曼猜想。质数包括2，3，5，7，11，13，17，19等等。如果你写下每个正整数的因数，你会看到质数，它们是只有两个因数的数。

让我们看看一些较大的质数：

101，103，107，109，113，127，131，137，139和149。

从一个质数到下一个质数的跳跃，它们似乎是相当随机的。有时两个质数是直接相邻的。像101和103这样的孪生素数；但是有时候，它们之间会有巨大的间隙，像113和127。

这里有没有底层的结构？我们能否预测下一个质数的出现的？这就是黎曼ζ函数出场的时候。

质数与黎曼ζ函数的零点相连。ζ函数是从复数到复数的函数。这意味着，对于任何复数的输入，将得到一个复数作为输出。例如，输入2，输出π平方除以6。输入负1，输出负1除以12。输入负2，输出0。所以数字-2，是黎曼ζ函数的一个零点。

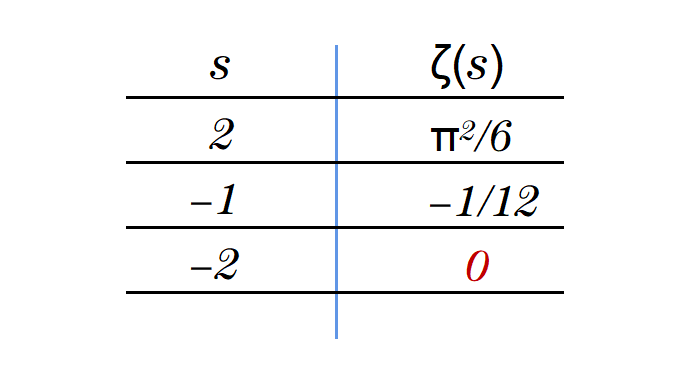
如果把所有这些零点作为复平面中的点，有些很容易计算，如-2，-4，-6等等，也就是负的偶数。

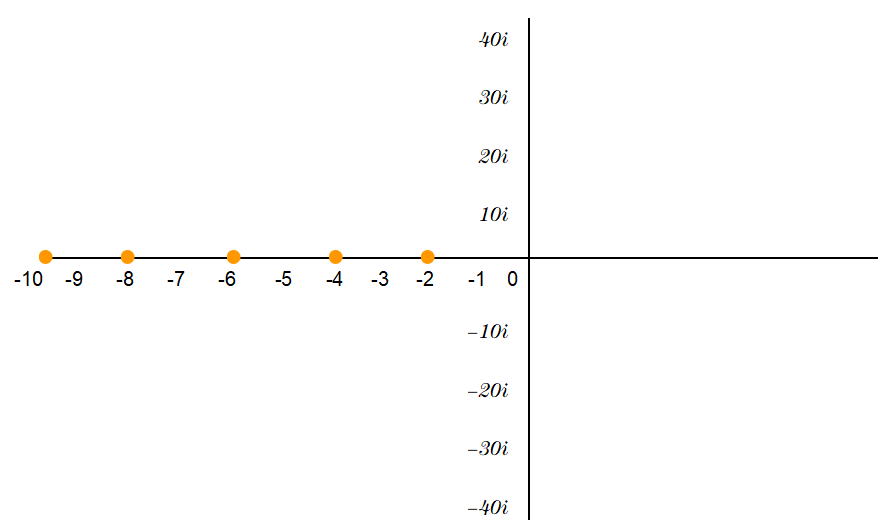
这些被称为平凡零点（trivial zeros）。其他的零点，被称为非平凡零点（non-trivial zeros），都包含在所谓的临界带（critical strip）中。

意思是，ζ函数零点的实部，在0和1之间。黎曼猜想声称，所有非平凡的零点，实部都等于1/2。

换句话说，它们都在所谓的临界线上。数学家们已经计算过，这些非平凡零点的前12万亿个，它们的实部都是1/2。

虚部呢？你可以计算它们，对于前几个零点，虚部大约是，14.1左右，21左右，25左右，这个数字序列被称为黎曼谱。

我们可以使用Sage计算更多的这些值。

要初步理解这些零点为什么如此有趣，让我们看看函数

这是一个余弦波，以14.1作为角频率，以对数x为变量。这里的“对数”是自然对数ln。让我们绘制函数f从x等于1到15的图形。

这看起来像是某种波，波长随x的增大而增大，但看看峰值！虽然不完美，但接近1、2、3、5和稍大于7的地方有峰值。在11和12之间有最后一个峰值。

现在我们再给函数f的定义加上一个项：

这个函数在大致是1、2、3、5、7，然后稍高于12的地方有峰值，

现在我们继续添加越来越多的项，

使用来自黎曼谱的数字构建这些余弦波。使用前十个项，就会有非常清晰的峰值，分别在1、2、3、5、7、11和13的位置。

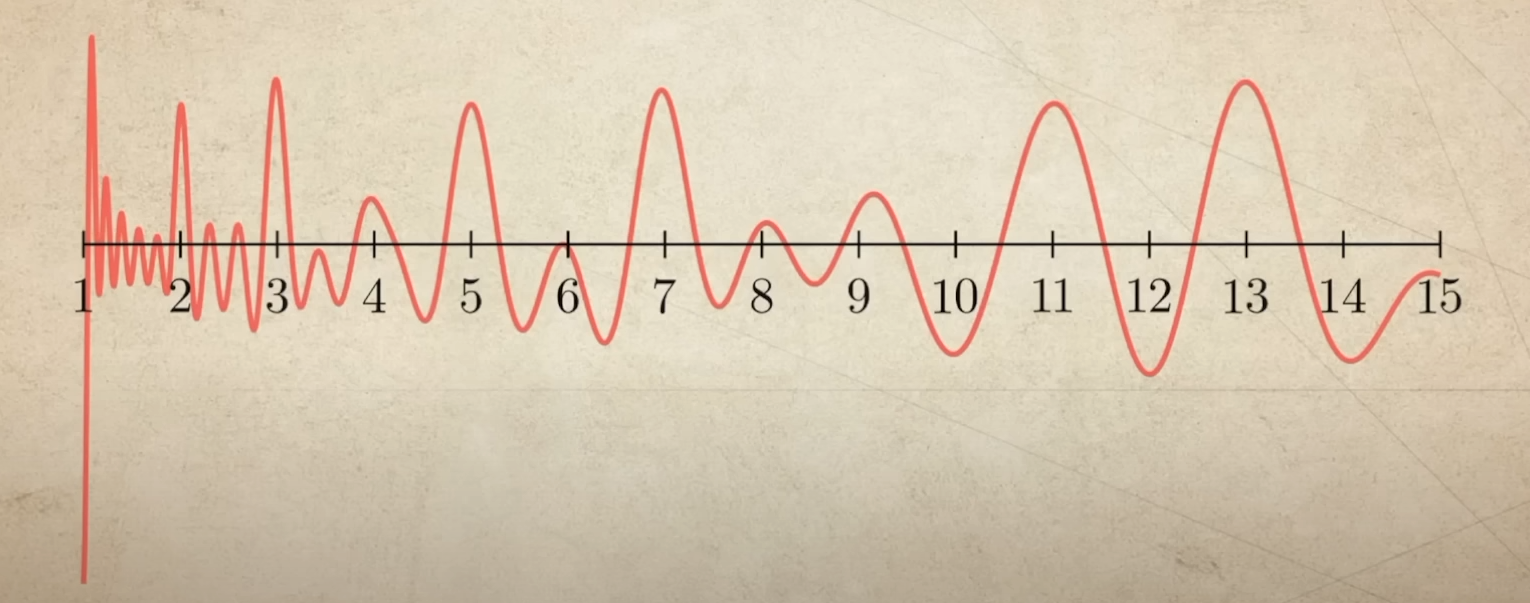
我们可以使用任意数量的项，让我们使用一百个项，并将这个图形扩展到x等于二十的地方，

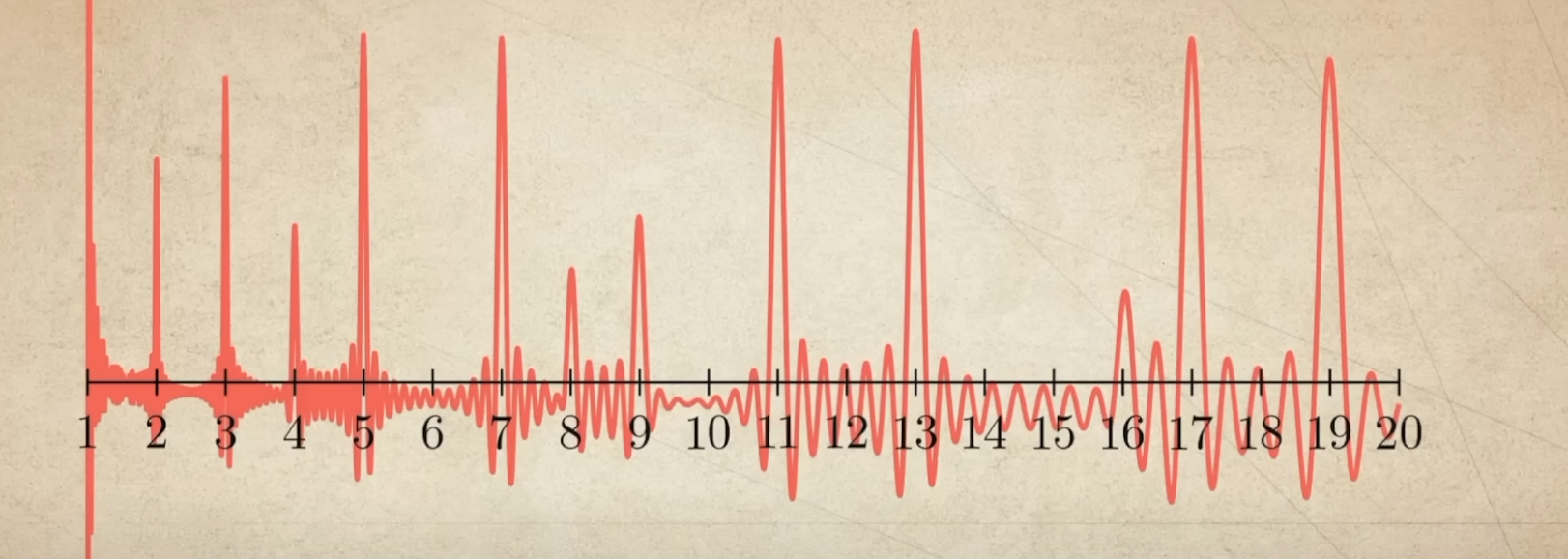
现在，也许你可以猜出这些小峰值是什么。在2之后，峰值出现在4、8和16。在3之后，峰值出现在9，然后会有更多的峰值出现在27、81等等。这些是2的幂和3的幂。总的来说，随着我们添加越来越多的项，并扩大x值的范围，所有的质数的幂都会出现尖峰。

这些图表是一个初步的小提示，虽然我们通常关注的是质数，但质数的幂对我们也非常重要。只需记住，这些图表，所有这些尖峰，并不是来自我们了解的质数，它们仅来自黎曼谱。所以显然，这里有一种连接，连接了黎曼谱和质数。这简直是疯狂的！质数与余弦波无关。如果你深入研究这种联系的细节，你想了解有多少质数在给定数值之前，比如说在二十或一百万之前，那么关键就是了解一个零值可能离临界线有多远。最完美和最美丽的情况应该是，所有的零值实际上都完全在这条线上。这个猜想就是黎曼猜想。

那么，我们如何证明黎曼猜想呢？这是一个价值百万美元的问题。关于黎曼ζ函数有很多书，关于黎曼猜想也有很多书。在其中的一些书里，你会发现人们尝试过的许多事情，以及可能在未来证明中起作用的许多想法的列表。当然，没有人真正知道最终会有什么效果。但是，我认为，如果你想阅读这些想法，最好的地方，也许是最好的地方，是布莱恩·康瑞（Brian Conrey）的一篇近期文章（RIEMANN’S HYPOTHESIS）。

康瑞是世界上黎曼猜想的顶级专家之一。他有很多很有趣的研究论文，但最著名的就是他证明了在临界带中至少40%的零值实际上在临界线上的那篇。

你可以自己阅读这篇论文（RIEMANN’S HYPOTHESIS），我只想强调我认为最有趣的一些想法。一开始就讨论了这个问题的历史背景，以及质数和零值之间的联系。有一小部分关于“我们为什么认为黎曼猜想是对的？”的内容，这也非常有趣。然后引入这个谱解释的想法，

意思是零值可能是某个算子的特征值。关于证明黎曼猜想的一些初步想法，听起来很有趣。然后我想强调这个第16节，

魏尔的显式公式和正性标准。17是李氏准则，

然后与函数域ζ函数的类比。另外，请关注Selberg类的概念。那是尝试写下一个L函数的公理的尝试。这种L函数的族的想法很重要，而且再次出现了"正性"这个词。正性确实是通向黎曼猜想任何未来证明的关键一步。最后，最后一部分，或者倒数第二部分，随机矩阵理论，这是一个超级有趣的研究领域。

总的来说，也许最重要的三个想法是，

第一，我们应该研究所有的L函数，而不仅仅是黎曼ζ函数，因为有一些模式和现象，如果你只研究黎曼ζ函数的话，是看不到的。

第二，关注这个正性的概念。这是对黎曼猜想的几种普遍方法之一，适用于一般的L函数，而不仅仅是黎曼ζ。

第三，重新审视与函数域的类比。与函数域ζ函数的类比，其中黎曼猜想已经被证明是真的，是我们相信黎曼猜想是真的主要原因之一。这也是新想法的主要来源，寻找隐藏的F1-几何。

后面，我们将研究L函数的来源。L函数来自我们称为原始对象的东西。我们也将研究另一个重大问题，那就是朗兰兹计划。