二重积分、三重积分，是很多学生在学习高等数学时的懵点，公式能理解，但不知道为什么能这样求，二重积分为什么能求出体积？

如果只是考研的话，只需要记住这个公式，记住运算步骤，到时候直接套就行了。

但心里总还是有个疙瘩在，它这个求法的背后底层逻辑是什么？

本篇就彻底带大家理解，好让多重积分的理念在脑海里如同呼吸一样自然。如果你做不到这点，仅仅知道公式，那么以后更高级的理论如多维空间的建模、场论、傅里叶变换等等你都理解不了，高等数学仅仅是基础数学，靠死记硬背的话，你花一辈子都背不完。

先回顾下最简单的定积分。

定积分的公式是这样：

这个公式的意思，是以f(x)这函数为界与x轴围成的从a到b这个区域的面积，表述可能不严谨，图大概就是这样：

而结果表达式是：

而f(x)其实是F(x)的导函数，其实就是导函数的逆运算。

然后把b跟a代入到x，那么这个面积的最终表达式就是：

F(b)-F(a)

这个表达式算出来就是个常数，因为里面的变量x都被积分上下限替代了。

相信学完定积分的，对这个应该很理解。

其理念就是每个x值都有对应的f(x)值（或者y）

而每个y值都可以看成有长度但面积无穷小的一小块区域的面积。

其实就是dF(x)

它虽然有长度，但面积是无穷小的，那也意味着这个区域内却有无穷多个这样的无穷小区域。

也就是它这个区域的总面积，是由无穷多个无穷小的区域面积相加起来得出的数。

至于为什么无穷多个无穷小相加会是个常数，这是很高级的数学问题，我会在别的文章详细解释。

接下来在教材里面，会有个经典的例题，就是用定积分求体积。

题目大概是这样：

给了一个一元函数f(x)，在x轴上截取a点到b点形成与f(x)围成的区域，也就是像上图那样。

然后把它放到一个三维直角坐标系里，把这个截取的区域，以x轴为圆心轴，旋转360°，形成了一个物体，求这个物体的体积。

图示大概是这样：

总之得出类似一个花瓶这样得物体。

求这个物体得体积V。

其思路就是，在任意一点，那把刀以垂直于x轴得方向一刀切下去，得出得横截面一定是个圆。

那么可以看成，这个物体，是由无穷多个圆面“积”出来得。

每个圆面看成是个体积无穷小的区域。

而每个圆面的面积跟什么有关呢？跟x有关。

因为每个x对应的y值（或f(x)值），就是这个圆面的半径。

那么其实这个圆面的面积，就是

不同的x值对应不同的圆面积，而把这些圆面“积”成体积，也就是对被积函数从a点到b点求对x的积分。

所以这个体积的表达式就是

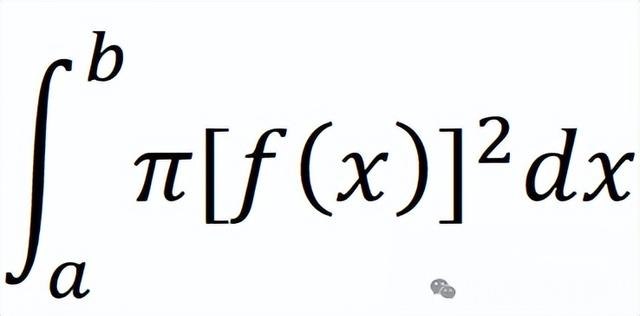
以上就是定积分求体积的思路，很简单，如果你连上面内容都理解不了，那么不用往下看了，后面多重积分你肯定理解不了的。

接下来就是二重积分。

二重积分也是求体积。

简单来讲，就是求一个二元函数f(x,y)，在某个xy的取值区域，形成的z值“积成”的体积。

（我表达也许不是很严谨，但这是为了方便大家理解）

首先二元函数的图像，是要用三维直角坐标系来显示，大概是这样：

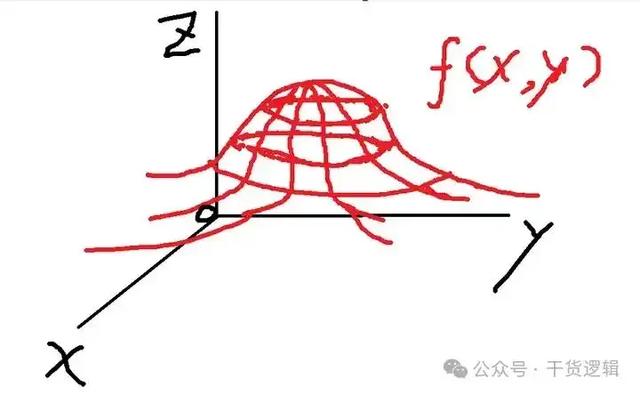
这是一个立体图，你可以想象成一个帽子这样的物体。

不同的x,y值，对应不同的z值，形成的一个凹凸不平的面，就是二元函数f(x,y）的图像。

而二重积分，其实是求这个物体的体积：

这个物体的顶面，是二元函数f(x,y)形成的面。

而现在照着底部区域Dxy，对着这个二元函数形成的面切下去，形成的一个物体。

现在求这个物体的体积。

这个思路是怎样呢？

先简单一点，我们假设现在底部区域Dxy由x=a,x=b, y=c,y=d这几条直线围成的区域。

现在，我们拿一把刀，以平行于y轴的方向，在这个a点到b点之间区域任意一点切下去，得出一个截面，如图：

如图，这个绿色区域，就是它的横截面。

我们现在求它的面积。

因为这个刀法，是平行于y轴切下去，所以x是个固定值，我们可以把它看成常数。

我们假设，这个刀就是沿着x=3这条直线切下去的。

那么这个留在f(x,y)这个函数图像形成的面的切痕的表达式，就是

f(3,y)

等于是把常数3代入到x里面，使x成为固定常数3.

而这个f(3,y)的函数图像，其实就是这样：

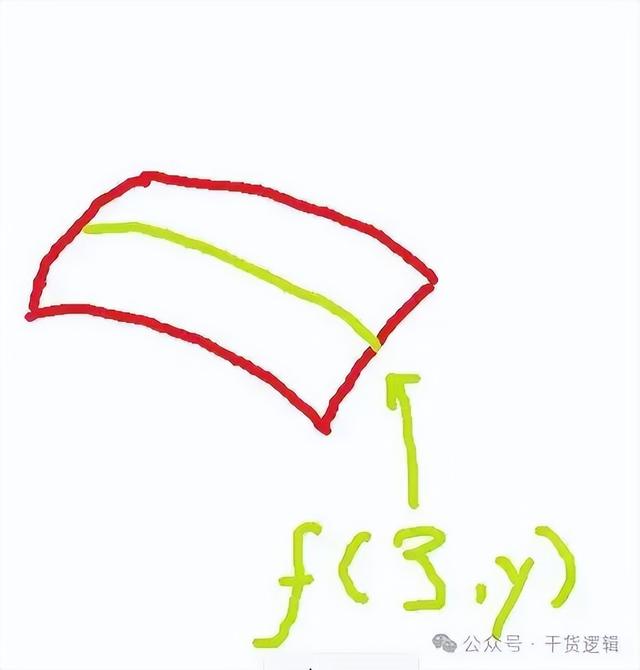
它就是在f(x,y)这个曲面上的一条曲线。

现在我们想要求这个横截面的面积，实质上就是在被积函数f(3,y)在c点到d点对y求定积分。

其表达式为：

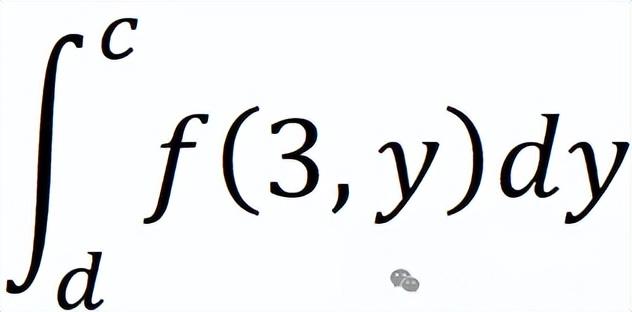
其实这个是对一元函数求定积分，因为x值是常数嘛，也就是对一元函数的求导逆运算。

求出结果的表达式为：

这个算出来的值，就是这个横截面的面积。

因为给了x=3这样的固定值，而y值最终被定积分上下限c,d替代，所以这个式子最终能求出来一个常数。

现在我们思考下，这个物体的体积，是不是由这个无穷多个横截面“积”出来的？

而这些横截面的面积，是不是只和x有关？

你瞧，对于x不同的取值，会得出不同的面积。

我们可以取x=4,x=5,x=6等等。

所以，这个横截面的面积大小，其实是自变量为x的一元函数。

这时肯定有同学要问了，那么y呢？你忘了y啊！y不是变量吗？为什么只剩下x了？

因为这个定积分求出来，y值最终会被积分上下限取值给替代掉，你会发现这个面积的表达式里面不存在y这个字母了。

所以，对于任意横截面面积的表达式，就是

F(x,c)-F(x,d)

所以，这个横截面的面积，只和你沿着x等于几的切法有关，它是只含x作为变量的一元函数。

其实这就回到了前面定积分那个简单例题，那么旋转体形成的花瓶的体积。

这个花瓶的体积是由无穷多个圆面“积”出来的，每个圆的面积，其实只跟x的取值有关，不同x的取值对应不同的半径y，也求出不同的圆面面积。

同样的，在这里不同横截面的面积只和x有关，而这个物体的体积，就是由这些无穷多个横截面“积”出来的。

所以，我们只需要对这个横截面面积函数作为被积函数，在a到b范围内对x求积分，最终就能得出这个物体的体积。

也就是：

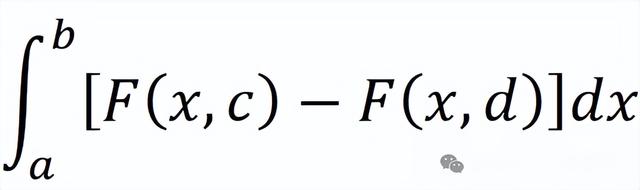
等于是又求了次定积分，所以叫二重积分。

我们把上述的两次积分，写成一个表达式就是：

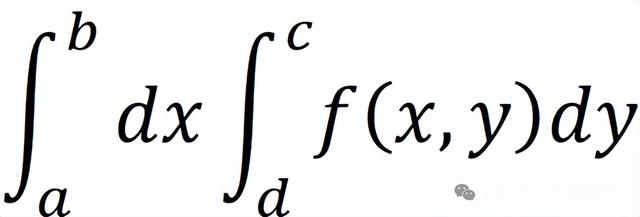
记住，多重积分计算，是从右边开始，从右往左算。把最右边的积分算出来，套入左边的积分表达式，然后再算。

也可以这么表示：

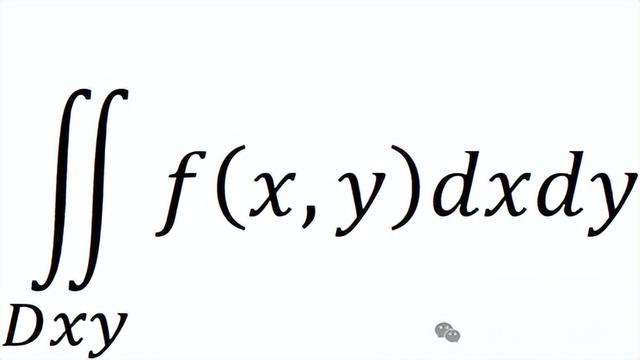
然而，有些时候，那个底部区域的范围，并不是那么简单的给出四条分别垂直于x轴y轴的直线。

例如，底部区域是由x=a, x=b，y=d, x+y=3,这三条支线围成的区域。

如图：

那么这时候，这个二重积分的函数表达式就变成这样：

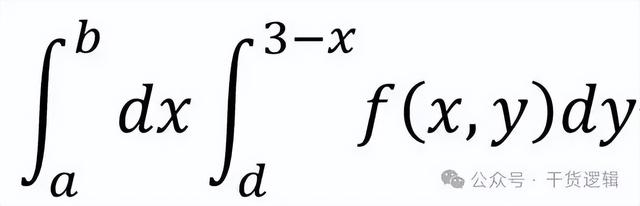
或是

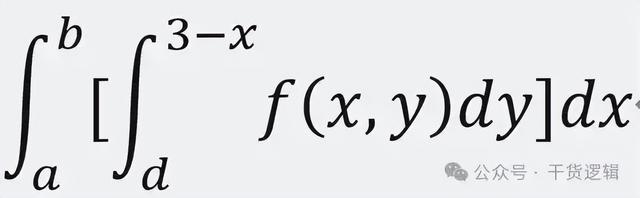
你会发现那个求横截面面积的定积分表达式里面，积分上限不再是一个常数，而是一个3-x的函数表达式。

也就意味着，积分上限也是随着x变动而变动。

这很好理解。

我们同样拿一把刀，以平行于y轴的方向，在x=a与x=b之间切下去。

如图：

你会发现，这切出来的横截面的右边那条边，是x+y=3这条直线与你的刀相交的点为起点。

所以，对于不同的x取值，对应了不同的积分上限，这个积分上限就是3-x。

所以，最终这个横截面的面积表达式就是：

F(x,3-x)-F(x,d)

它依然是个只含x作为变量的一元函数。

所以，二重积分求体积的通用表达式就是

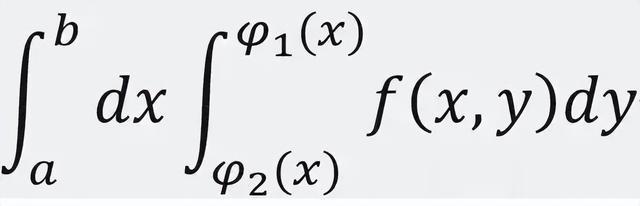
以上就是二重积分求体积的思路。

下面就讲到三重积分，如果你对上面的内容还是不明白，那么就先不要往下看，把上面看懂了再继续往下看。

三重积分，可以看成是对三元函数求积分。

一元函数求积分，也就是定积分，其取值范围是x的变量，它是一条线，是一维的。

二元函数求积分，也就是二重积分，其取值范围是x,y的变量，它是一个平面区域，是二维的

而到了三元函数求积分，就是三重积分，其取值范围是x,y,z的变量，它是一个三维体区域，它是一个立体物体，这个立体物体从内到外的每一个点就是x,y,z的取值。

而三元函数f(x,y,z)的函数图像，我们人类是无法画出来的，因为它需要在一个四维坐标系表达出来，而我们人类是无法想象出四维空间，所以三元函数只能给出表达式。

但它的取值范围就可以画出来，就是上面说的，是一个立体空间区域。

对三元函数求积分，其现实意义可以看成：有这么个物体，这个物体从内到位每个点的密度可能都不一样，现在要求出这个物体的总质量。

那么这个求法，就是对三元函数求积分，也就是三重积分。

其实就是每个不同的(x,y,z）坐标点，都对应了一个值f(x,y,z)，把所有的这些值“积”出来，就是三重积分。

三重积分有三种求法，分别是投影法，截面法，球面法。

先说投影法：

现有三元函数f(x,y,z), 其给定x,y,z的取值范围，是一个长方体，底部由x=a,x=b,y=c,y=d组成，高为h，如图：

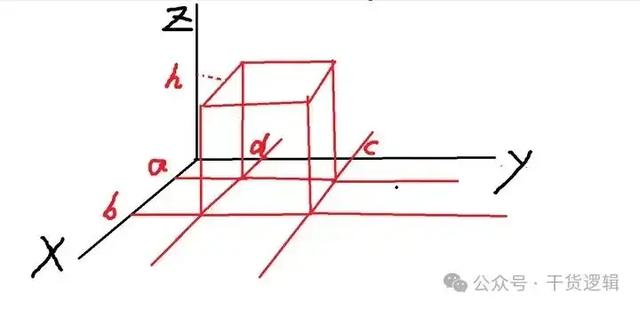
现在求这个函数的三重积分。

投影法的思路是，先在底部区域内任意取一点（x,y)。

（严谨的讲，这一点的正确坐标表达式是（x,y,0))

然后从这个（x,y）点出发，做一条垂直于xoy平面的线，一直到三元函数积分区域的顶部。

用被积函数f(x,y,z)对这条线求积分，其实就是对z求定积分。

因为这是个长方体，所以比较简单，其积分上下限分别是z=h，z=0（h就是这个长方体的高）

这时x，y的取值是固定的。

其表达式为：

这个表达式的意思是，把x,y看成是一个常数，，z是这个式子里的唯一变量，并对z求积分。

或者我就直接给个取值吧。

取一个xy取值为（4，5）的点。

那么这个表达式就是：

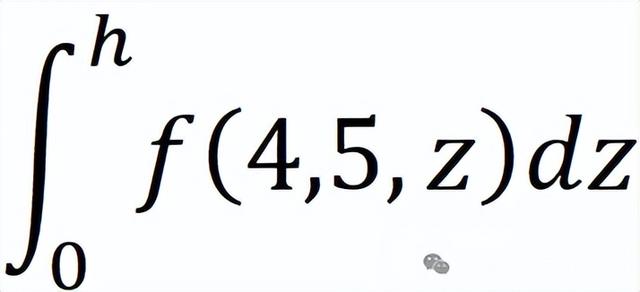
其结果就是

F(4,5,h)-F(4,5,0)

最终得出来是个不带任何变量的常数。

这么做的意义是什么呢？

首先，如果f(x,y,z)是个密度函数，求这个函数的三重积分其实就是求这个长方体的总质量。

而上面求出来的结果，你可能以为是这条“线”的质量，其实不是，这条线的质量依然是无穷小的，我们可以看成这是线密度。

而最终，我们把这个取值范围内，任意（x,y）取值所发出的射线，把它全部“积”起来，它有无穷多个，也就是把无穷多的线密度积出来，就是求出了这个长方体的总质量。

(我之所以举质量跟密度，是为了让大家好理解，其实你可以完全抛开质量跟密度。

我们把被积函数f(x,y,z)的原函数记为G(x,y,z)， 也就是我们把三重积分的最终结果先标记为G(x,y,z)

对于任意给定的（x,y)取值，都有个对应的值

但我为了方便大家理解，我后面会把这个

说成是线密度）

于是，任意一个点（x,y），都有对应的一个线密度。

而这个线密度的大小，只和x,y的取值有关，跟z无关。

因为求定积分的时候，z已经被积分上下限代入了，所以最终表达式里面不含变量z。

这个定积分求出的结果就是

F(x,y,h)-F(x,y,0)

你会发现，会得出一个只含x,y的函数表达式。

也就是一个二元函数，我们就把它记为g(x,y)吧。

而它就是线密度函数。

不同的（x,y)取值，对应不同的g(x,y)值。

我们就可以画出这个二元函数的图像。

g(x,y)值就是线密度值，并且xy的取值范围也有了，把所有这些无穷多的线密度值“积”起来，就是总质量。

也就是最终我们只需对这个g(x,y）求二重积分，就求出这个长方体的总质量。

也就是f(x,y,z）的原函数G(x,y,z）

把前面所有步骤结合起来。

这求长方体质量的三重积分的表达式就是：

或者可以这么写：

但这还不是通用的表达式。

像前面二重积分一样，有时候三重积分的积分区域，并不是那么规则。

例如，f(x,y,z)的取值范围，是一个原本的长方体，被一把刀沿着z-y=3的线，垂直于z0y平面的方向劈下去，形成的物体，如图：

这时，对被积函数f(x,y,z)求z的定积分的下限，不再是常数，而是带有变量z的表达式。

对于不同的xy取值都有不同的下限。

那么三重积分的表达式变为：

所以，通用的表达式应该是：

以上就是投影法求三重积分。

除此之外，还有截面法。

其实如果你理解了前面投影法，那么截面法也很好理解，只是思路顺序变了而已。

界面法的思路，是在z取值范围内，拿一把刀以任意z的取值作为高度，以平行于xoy平面的水平方向切过去，得出一个平行于xoy平面的横截面，如图：

这时候，z是给定的，可以看成一个常数。

求的就是在给定z取值的情况下，得出一个有xy不同取值形成的面。

得出一个二元函数：

例如给定z=5，那么其二元函数就是：

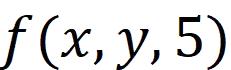
对这个二元函数求二重积分，表达式便是

这个表达式最终算出来是个常数。

其结果是：

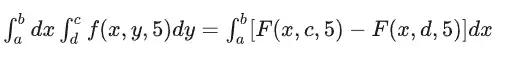
最后把上下限b跟a代入到x，最终式子里没有一个变量，全是常数，得出的结果也是常数。

我们把这个二重积分求出来的值称为面密度。

也就是说，不同的z取值，对应不同的面密度。

这个面密度只跟z取值有关。

那么这个面密度的函数表达式为：

而这个表达式最终会得出只带变量z的函数表达式。

而最终这物体的总质量，就是把无穷多个面密度“积”出来。

那么，我们只需对这个只带变量z的函数表达式再求一次定积分，就能求出其总质量。

所以，截面法的通用表达式就是：

其实，如果你理解了三重积分，用同样思路，可以用在N重积分。

本质上这些运算，是一步步的降维。

最终把结果以一维的状态呈现。

什么是一维，常数就是一维，一个具体的数值。

例如在二重积分里，我们先求出截面面积的函数表达式。

实际上让每个x值对应一个面积值，让这个体积函数成为了一元函数。

如图：

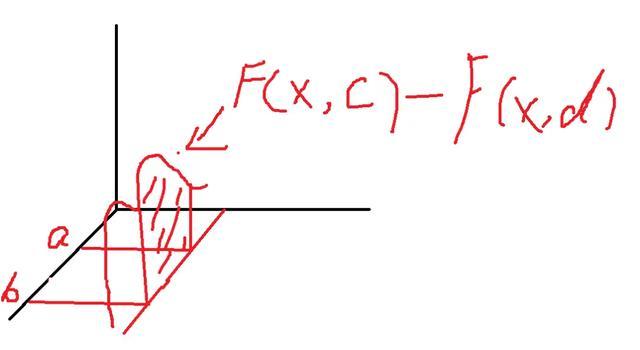
fxy(x,y,z)

然后对这个一元函数求定积分，最后形成了一个具体的数值。

三重积分也是，那个投影法，本质上是把原来的 物体，压成了一个面，面上每个点代表了一个原来物体的线密度。

而截面法，就是把每个面密度，压成了一条线，每条线代表一个面密度。

所以，对于后面的N重积分，本质上都在重复同样的方法，就是不断的“降维”。

=========================================================

想不到那么多人点赞，感谢大家的支持，那我就把这贴作为长期更新贴，继续讲下去。

接下来是如何像呼吸一样自然的理解第一类曲线积分

刚开始学曲线积分，许多同学最容易懵逼的点，就是为什么f(x,y)能表示成曲线？

因为我们学曲线积分前，学的是N重积分。

在学二重积分的时候，二元函数我们用f(x,y)来表示，它的函数图像是一块面，就如同一块有凹凸的布浮在三维直角坐标上，如同这样：

上图的x,y是任意取值。

那么到了曲线积分，怎么又能用f(x,y)来表示曲线呢？

难道这两块是不同的知识体系？

其实，空间曲线的完整表达式，应该是：

f(x,y），y=g(x)或x=g(y)

或者直接这么表达：

f(x,g(x))

它等于是让x,y不再任意取值，而是给定了x跟y之间的函数关系g，然后在套入到二元函数f里面求出z。

于是，它的函数图像应该是这样：

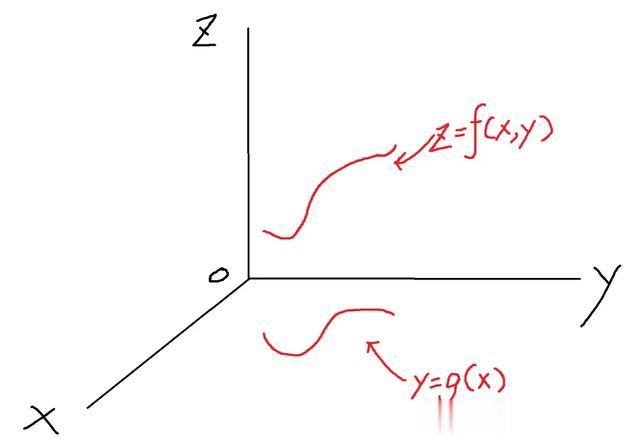
如果没给出x跟y之间的函数关系g(x)，那么原本f(x,y)就是一块浮在xoy平面之上的一块布，就如同前面第一张图那样。

而一旦规定了x跟y的函数关系g(x)，就形成了现在这一张图。这相当于拿着一把刀，对着f(x,y)这块布，沿着g(x)的轨迹切下去。这块布上的切痕，就是曲线函数f(x,y)

而y=g(x)，则是f(x,y)在平面xoy上的投影。

而第一类曲线积分，就是在y=g(x)上从一个点到另一个点之间，例如a点到b点，把每个（x,y）点，对应的z值“积”出来。

也就是求下图阴影部分面积：

它的函数表达式为：

或者：

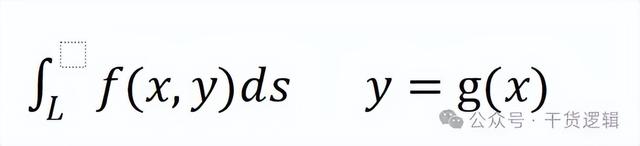
亦或者x跟y的函数关系是用参数方程表示：

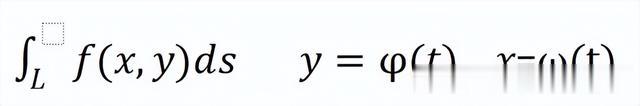
为了方便理解，你可以看成，它相当于给出了g(x)上每个(x,y)点的密度z（或者f(x,y))，用积分的方式求出了这条g(x)曲线的质量。

其中，这个公式里L表示的是g(x)的弧长，或者说是空间曲线f(x,y)投影到xoy平面上的弧长。

而ds，指的是曲线微元，或者弧微元，是指g(x)这条曲线的长度微分，或者说是空间曲线f(x,y)投影到xoy平面上的弧的长度微分。

在这里同学们很容易犯的错误，就是把L跟ds分别表述成，是曲线f(x,y)的弧长，跟曲线f(x,y)的弧长微分，因为式子里的被积函数是f(x,y)嘛！这是错的！正确表述应该是f(x,y)投影到xoy平面上的g(x）曲线的弧长与弧长微分。

还记得在二重积分里，积分区域是用xoy平面上取一小块平面来作为积分区域嘛？在这里同样也是在平面上取平面弧的一小段作为积分区域。

其中，ds是简化了的表达，完整表达应该是：

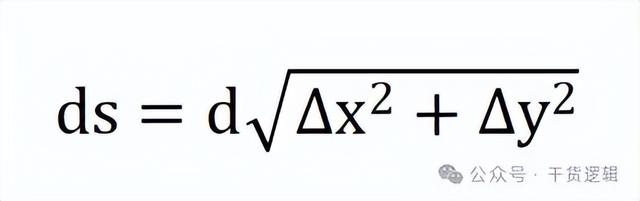
为什么呢？

因为弧长的微元，看成是取弧长极小的一段，按照勾股定理，这一小段的变化，可以看成是两个直角边的平方和的开方：

那么一类曲线积分更完整的表达式应该是：

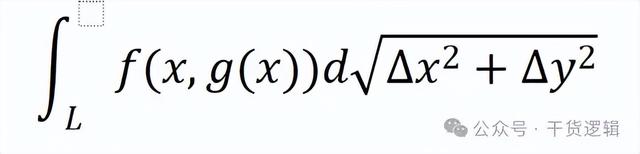
那这个公式该怎么求呢？

我随便举一个，例如

该怎么运算呢？

一些同学就可能先求出原函数，也就是导函数逆运算得出原函数为 12x2

同学你错啦！

我们学习积分，很重要的是要搞懂什么是被积函数，什么是积分对象。

如果积分对象是x，也就是这式子后面跟的是dx而不是ds，那么这个答案没毛病。

然而后面跟的是ds，那么积分对象是弧长元素，就不能直接这么算了。

该怎么算呢？

思路就是把积分对象转换，如果能把积分对象变成dx，那么就好办了。

按照教材，这时候我们可以用第二类换元法。

构建一组参数方程：

通过用中间变量t，来表达x与y之间的函数关系。

因此：

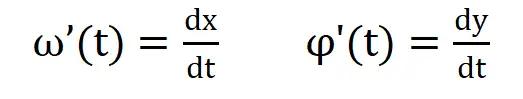
那么换算下，就可以得出：

这样，我们就可以把原来的积分公式里面的变量换成t，积分区域L换成了t的取值范围，我们就设α≤t≤β

而因为

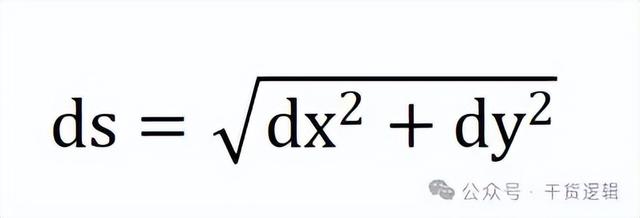
那么按照上面，我们把它换成只含变量t的方程：

然后我们可以把根号里面的dt提出来，变成：

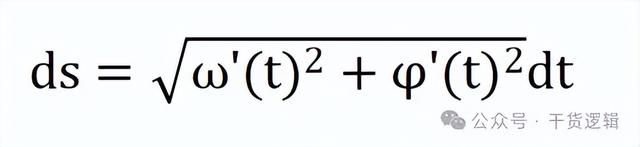
那么原来的积分公式，就可以变成这样：

这样，我们就能把原来的积分公式，变成只含变量t的函数，这样就能按一般的定积分运算来算出来。

而如果题目直接给出了x,y的函数关系y=g(x)

那么我们就可以构建中间变量为x的参数方程，这样最后的积分对象就是x了：

因为对x求导就是1，那么上面的ds，就可以变成：

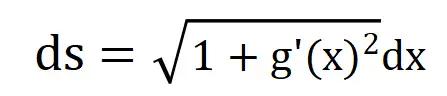
因为前面这个函数图像：

对应的表达式，就是：

这样就能算出这条曲线的总质量。

而如果求弧长L，其实就是上面这个通用算法的特殊形式。

就是把f(x,y)=1

也就是对常数1求曲线积分，或者说这个曲线的密度每一点都为1

那么表达式就变成：

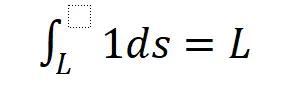
为什么这样就能求出弧长L?

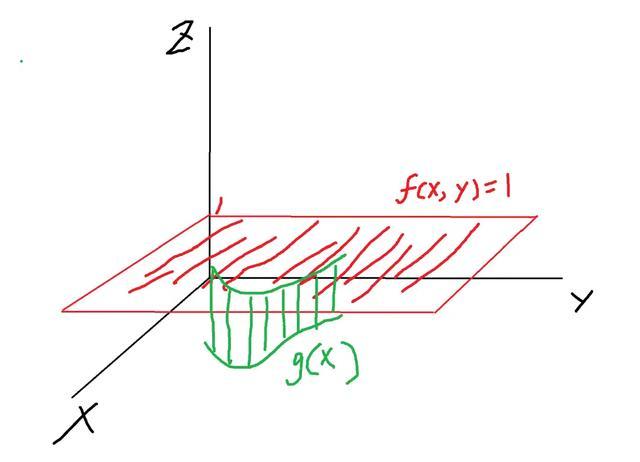
首先，如果不给定x,y之间的函数关系，那么f(x,y)=1的函数图像是这样的：

就是一块平行于xoy平面，离xoy平面距离为1的平面，这个平面是无限大的。

而一旦给出了x,y的函数关系y=g(x)

就相当于在f(x,y）这个平面上，拿把刀按着g(x)的曲线切，这个切痕就是f(x,g(x))=1

并且，它跟xoy平面上的投影曲线g(x)是完全一样只不过在不同平面，并且相互平行，相互垂直距离为1，如图：

而f(x,y)=1的曲线积分，就是求上图绿色阴影部分的面积。

如果把这个绿色的面拉直，它就是一个长方形面积。它的长为曲线g(x)的长度L，高为1

而面积除以高，就是长。

高就是f(x,y）或者z的取值，它恒为1嘛。

所以面积除以1，得出的数值就是L的长度。

所以

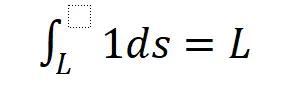
其实这个弧长求法，我觉得才是这个一类曲线积分里面最具现实意义的知识点。

因为有了这个，于是平面中，任给的一条连续的函数曲线y=g(x)，从某个点到某个点的这个曲线弧长，都可以用下面公式求出：

当然，不等式右边的根号外的那个1可以直接去掉，我是为了让大家直观理解，因为f(x,y)等于1，所以右边直接用1取代了f(x,y)

上面就是二元曲线积分，下面简单讲讲三元曲线积分。

其实很简单。

三元曲线的函数表达式为：

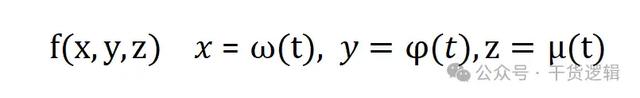
亦或者：

还记得在三重积分里，积分区域是三维坐标系里的一个立体物体吗？而三元函数的函数图像我们是想象不出来的，因为它需要四维坐标系，我们只能想象并画出其积分区域。

而x,y,z一旦给定了函数关系。

那么实际上，f(x,y,z)的函数图像就变成了在四维坐标系的一条曲线，当然我们画不出来。

但我们可以画出它的三维坐标系的投影，它就是一个悬浮在立体空间区域的弧。

而积分区域L，就成了而这条立体区域曲线的长度。

还记得前面二元曲线积分，L是指f(x,y)投影在xoy平面的曲线g(x)弧长；到了这里，三元曲线积分，L就成了三维空间里的弧的弧长。

而三元曲线积分如何用图像表示呢？大概是这样：

很抱歉，无法画。

因为它是这条三维曲线的每一点，到四维曲线上对应点的距离的积分。或者说是四维曲线的每一点到三维空间投影的每一点的距离，再把它积分。

四维曲线我们是想象不出来的，所以也无法画。

而ds，就等于：

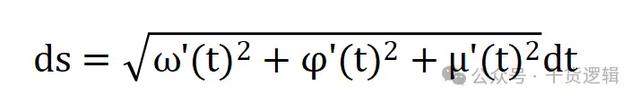
那么，三元曲线积分的完整表达式，就可以这样：

以上就是一类曲线积分，在下一篇中，会带大家呼吸般自然的理解第二类曲线积分与格林公式。

未完待续，持续更新