曾经有个选择摆在我面前,我没有好好把握,直到我知道背后的真相后,我追悔莫及。
今天要学习一个“反直觉”的问题。先来参与一个游戏吧。
有三个空盒子,只有一个里面有奖品。抽奖人选择一个后,开奖人会打开一个空盒子,问抽奖人要不要换选中的盒子。如果你是抽奖人,你会怎么选择呢?
表面上看,会有以下这几类的直观感受
1. 盒子本来就有三个,我在最开始选择时,选中的概率就是1/3,开空盒子只是干扰项,所以,不管我换不换,中奖概率都是1/3。
2. 开奖人剔除了一个空盒子后,剩下两个盒子,其中只有一个有奖品,现在就是二选一,所以,不管我换不管,中奖概率都是1/2。
3. 如果我不换,那就是最开始的三选一,中奖概率是1/3,如果换,那就是二选一,所以,要换。
4. 刚开始选择一个,概率是1/3。把另外两个看成一个组合,这样概率是2/3。进一步分析,由于另外两个由于剔除掉了一个空盒子,所以剩下的1个必然是2/3。
为了解决这个问题,我尝试用编程方式来模拟并解决。
public void GuessTest(){ var times = 10000; var index = 1; var rd = new Random(); var sucess = 0; while (index <= times) { var dic = new Dictionary<int, int> { { 1, 0 }, { 2, 0 }, { 3, 0 } }; // 1,2,3 随机数 var num = rd.Next(1, 4); // 设置奖品所在盒子 dic[num] = 1; // 抽奖人选择盒子: 1,2,3 随机选择一个 var selection = rd.Next(1, 4); // 剔除一个非中奖号 var toRemove = dic.First(e => e.Key != selection && e.Value == 0); var newDic = dic.Where(e => e.Key != toRemove.Key).ToDictionary(e => e.Key, e => e.Value); // 被测者,更换为另一个 selection = newDic.First(e => e.Key != selection).Key; // 如果不换,则这行代码注释掉 if (dic[selection] == 1) { sucess++; } index++; } var rate = sucess * 1.0m / times; Console.WriteLine($"猜中{sucess}/{times},猜中率为{rate.ToString("P")}");}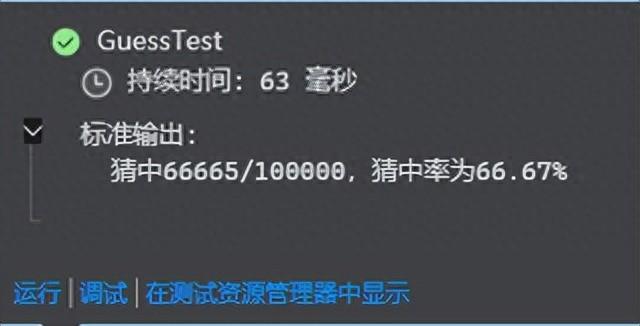
最终结果令人惊奇。换号码后,中奖概率为2/3。为什么会有这么非直觉的结果呢?
经过后续查阅资料,原来这题可以用贝叶斯公式求解。
贝叶斯公式(Bayes'theorem)是概率论中的一个重要定理,用于计算条件概率。
贝叶斯公式可以表示为:
P(A|B)=(P(B|A)* P(A))/ P(B)
其中,P(A|B)表示在事件B发生的条件下事件A发生的概率,P(A)和P(B)分别表示事件A和事件B单独发生的概率,P(B|A)表示在事件A发生的条件下事件B发生的概率。
结合问题,我们可以使用贝叶斯公式来解释改变选择后获奖的概率是否更高。
假设抽奖者选择的是盒子1,开奖人打开盒子2,根据贝叶斯公式,问题就抽象为:
1. 选择1,打开2,奖品在1的概率P(奖品在1 | 选择1且打开2)=(P(选择1且打开2 | 奖品在1) * P(奖品在1)) / P(选择1且打开2)
2. 选择1,打开2,奖品在2的概率P(奖品在2 | 选择1且打开2)=(P(选择1且打开2 | 奖品在2) * P(奖品在2)) / P(选择1且打开2)
3. 选择1,打开2,奖品在3的概率P(奖品在3 | 选择1且打开2)=(P(选择1且打开2 | 奖品在3) * P(奖品在3)) / P(选择1且打开2)
看的有点绕,我们先把简单的数据计算一下:
P(奖品在1) = P(奖品在2) = P(奖品在3) = 1/3。
奖品在三个盒子的概率都是一样的,都为1/3。
P(选择1且打开2 | 奖品在1) = 1/2。
奖品在盒子1时,抽奖人选择了盒子1后,开奖人可能打开盒子2或者盒子3。所以概率为1/2。
P(选择1且打开2 | 奖品在2) = 0。
奖品在2,开奖人是不可能打开盒子2的,所以为0。
P(选择1且打开2 | 奖品在3) = 1。
奖品在3时,抽奖人选择盒子1后,开奖人必然打开盒子2。
P(选择1且打开2) = 1/2。
在汽车在原来选择的门后面的情况下,主持人打开另一扇门后面有山羊的概率为1;在汽车在另外两扇门后面的情况下,主持人打开另一扇门后面有山羊的概率为1/2。所以
这里分三种情况:
第一种,奖品在盒子1,这样开奖人开2或3,即(1/3)*(1/2);第二种,奖品在2,开奖人不可能打开2,概率为0;第三种,奖品在3, 开奖人开盒子2,即:1/3
所以:
P(选择1且打开2) = (1/3) * (1/2) + (1/3) = 1/2。
套上以上公式,可得。
P(奖品在1 | 选择1且打开2)=(P(选择1且打开2 | 奖品在1) * P(奖品在1)) / P(选择1且打开2)
= (1/2 * 1/3 ) / (1/2) = 1/3
P(奖品在2 | 选择1且打开2)=(P(选择1且打开2 | 奖品在2) * P(奖品在2)) / P(选择1且打开2)
= (0 * 1/3)/ (1/2) = 0
P(奖品在3 | 选择1且打开2)=(P(选择1且打开2 | 奖品在3) * P(奖品在3)) / P(选择1且打开2)
=(1*1/3)/(1/2) = 2/3
可见,换的机会是2/3,比不换的1/3高出整整1倍的概率。