我们所处的三维空间,由长、宽、高三个维度构成 ,这是日常生活中最容易感知的空间概念。在这个空间里,我们看到的每一个物体都具有长度、宽度和高度,它们共同勾勒出了我们生活的世界,赋予了物体立体感和空间感。
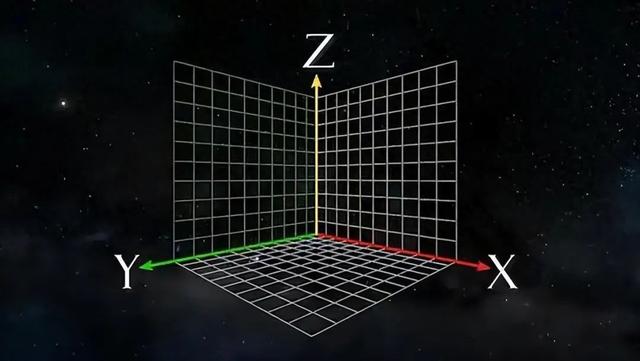
在三维空间中,物体的位置可以通过三个坐标(x,y,z)来精确确定,这使得我们能够准确描述物体在空间中的具体位置。我们能够清楚地知道一个物品在房间的哪个角落,一座城市在地球的哪个方位。三维空间的存在,为我们的生活、科学研究、工程建设等提供了基础框架,让我们能够理解和把握周围的世界。

与三维空间的直观感受不同,四维空间是一个更为抽象的概念,通常在数学和物理学领域被探讨。在数学中,四维空间被定义为在三维空间的 x、y、z 坐标轴的基础上,再增加一个维度,形成一个具有四个维度的空间。这就意味着在四维空间中,确定一个点的位置需要四个坐标(x,y,z,w) ,其中 w 代表新增的维度。

不过,这个新增维度究竟该如何放置,又以怎样的形式表现,至今仍然是个未解之谜,引发着无数科学家和学者的深入思考与激烈探讨 。
在物理学里,爱因斯坦的相对论提出了四维时空的概念,将时间视为第四维,与三维空间紧密结合,形成了一个不可分割的整体。在这个四维时空的框架下,时间不再是孤立存在的,而是与空间相互关联、相互影响。
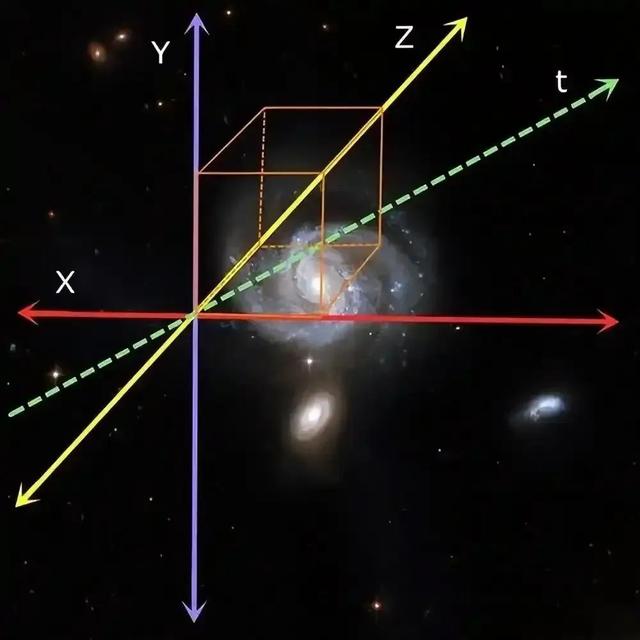
物体的运动和相互作用不仅涉及空间位置的变化,还与时间的流逝息息相关 。当一个物体在高速运动时,根据相对论,它的时间流逝速度会变慢,空间也会发生相应的扭曲。这种时间与空间的相互交织,深刻地改变了我们对宇宙的认知,让我们意识到宇宙的奥秘远比我们想象的更为复杂和深邃。
爱因斯坦的相对论对现代物理学的发展产生了深远影响,为科学家们理解宇宙的本质提供了重要的理论基础。它解释了许多以往无法理解的物理现象,如引力的本质、光线在引力场中的弯曲等。通过将时间纳入维度的范畴,相对论揭示了宇宙中时空的相对性和相互联系,让我们对宇宙的运行规律有了更为深入的认识。
从数学层面来看,三维空间通过 x、y、z 三个坐标轴构成的坐标系来定位物体的位置,这三个坐标轴相互垂直 ,形成了一个立体的坐标体系。在建筑设计中,设计师需要精确确定建筑物在三维空间中的位置和形状,通过三维坐标系,他们可以准确地描述建筑物各个部分的长、宽、高,从而进行详细的设计和规划 。在地理信息系统中,利用三维坐标系可以精确表示地球上的山脉、河流、城市等地理要素的空间位置和形态,为地理研究和资源管理提供了重要支持。
而在四维空间中,需要四个相互垂直的坐标轴(x,y,z,w)来确定一个点的位置 。然而,在我们的日常经验里,很难想象一个点上会有四条相互垂直的线,这是因为我们的感知和认知局限于三维空间。这种难以想象的情况,使得我们在理解第四维度时面临巨大的困难 。
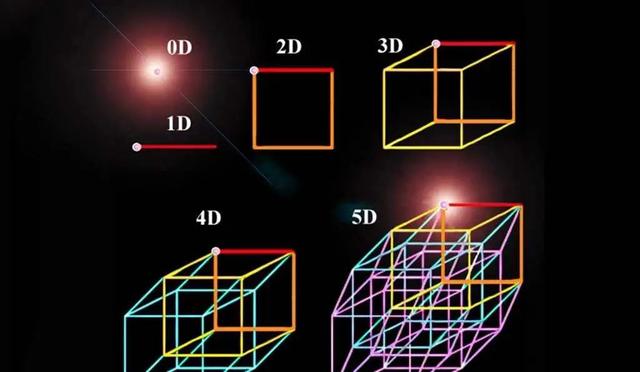
就像二维生物难以理解三维空间的高度概念一样,我们作为三维生物,在理解四维空间时也存在着认知上的障碍。尽管数学公式能够清晰地表达四维空间的坐标体系,但要在脑海中构建出这样一个抽象的空间,对大多数人来说几乎是不可能的 。
在三维空间中,我们熟悉各种基本的几何形状,如立方体、球体、圆柱体等。立方体由六个正方形的面组成,具有明确的长、宽、高;球体则是一个完全对称的立体图形,表面上的任意一点到球心的距离都相等;圆柱体由两个平行的圆形底面和一个侧面组成,具有独特的空间结构。这些几何形状在我们的生活中随处可见,构成了我们对空间形态的基本认知 。
当我们尝试理解四维空间中的空间形态时,情况变得更加复杂。
四维空间中对应的超立方体等抽象形状,其结构和性质超出了我们的直观想象 。超立方体在三维空间中的投影呈现出奇特的形态,它的各个面和棱的关系变得十分复杂,让人难以捉摸。超立方体的投影可能会出现多个立方体相互嵌套、重叠的情况,这些立方体之间的连接和变化方式,与我们熟悉的三维几何形状有着本质的区别 。
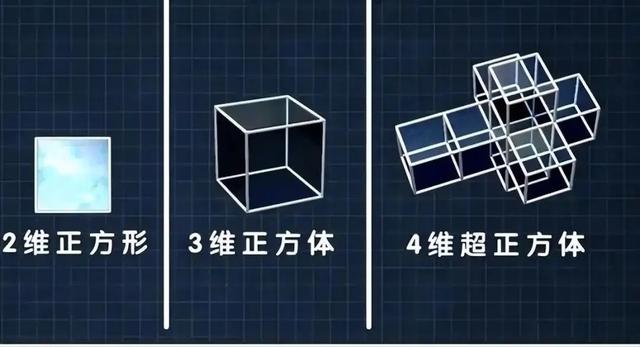
我们可以通过类比三维物体在二维平面上的投影来理解这种现象。一个立方体在二维平面上的投影可能是一个正方形,也可能是一个六边形,这取决于投影的角度和方式。同样地,四维物体在三维空间中的投影会随着投影方式的不同而呈现出各种各样奇特的形状 ,这些形状往往包含了更多的维度信息,使得我们在理解和解读时需要花费更多的精力和想象力 。
不同维度空间中,物理规律和现象有着显著的差异,这些差异不仅丰富了我们对宇宙的认识,也为科学研究提供了广阔的探索空间。在三维空间中,我们熟悉的牛顿运动定律和万有引力定律能够很好地解释物体的运动和相互作用。一个物体在不受外力作用时,会保持静止或匀速直线运动状态;两个物体之间的引力大小与它们的质量成正比,与它们之间的距离的平方成反比 。
当我们将视角拓展到四维空间时,这些物理规律的表现形式会发生有趣的变化。由于第四维度的存在,物体的运动轨迹和相互作用方式变得更加复杂。在四维空间中,物体可能具有更多的自由度,其运动方向不再局限于三维空间中的三个方向,这可能导致一些在三维空间中难以想象的物理现象 。物体之间的引力相互作用也可能不再遵循简单的平方反比定律,而是受到第四维度的影响,呈现出更为复杂的关系 。
弦理论作为前沿的物理理论,认为宇宙是由微小的弦构成,这些弦在十维或十一维的空间中振动,不同的振动模式对应着不同的基本粒子和物理现象 。
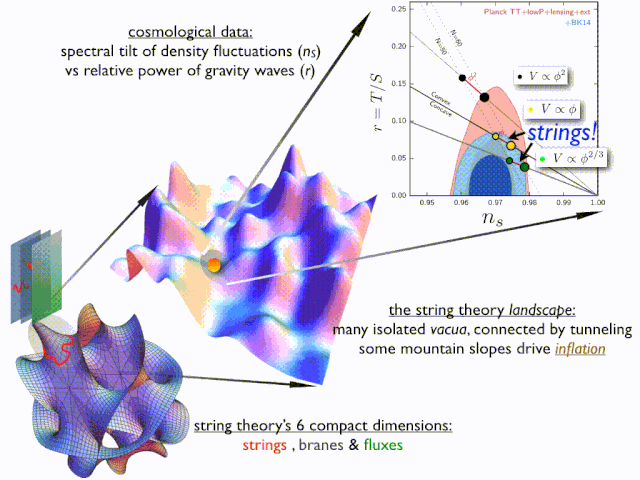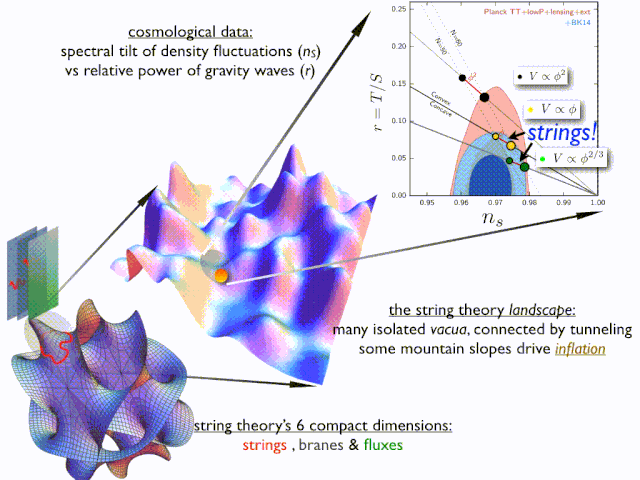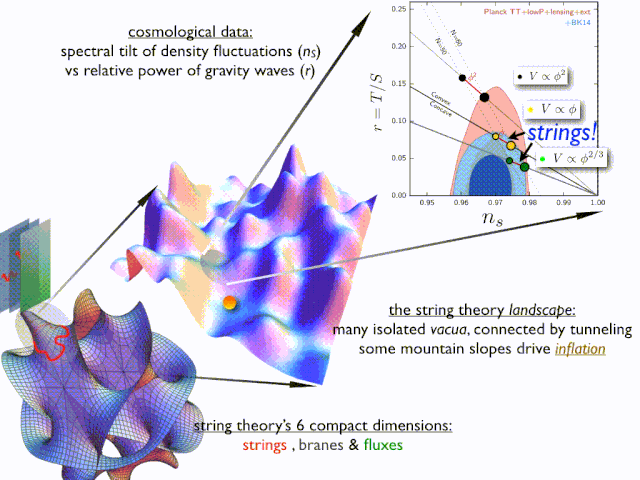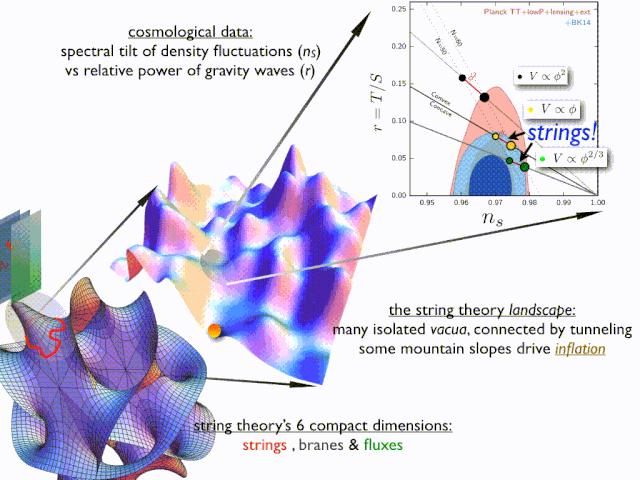
在这个理论框架下,四维空间是其中的一部分,它与其他维度相互关联,共同构成了宇宙的基本结构。弦理论的提出,为解释一些基本物理现象提供了新的视角,也让我们对四维空间在物理学中的重要性有了更深刻的认识 。尽管弦理论目前还处于理论研究阶段,尚未得到完全的证实,但它已经引发了科学界的广泛关注和深入探讨,为未来物理学的发展带来了新的希望 。
为了更直观地感受维度之间的差异,我们可以通过低维与高维的类比来进行理解。想象一下,在一个二维平面上,生活着一群只能感知长度和宽度的生物,它们的世界就像一幅扁平的画卷 ,没有高度的概念。对于这些二维生物来说,三维空间中的高度是完全无法理解的,就像我们难以想象四维空间中的额外维度一样 。
在二维世界里,一个封闭的圆形对于二维生物来说就是一个无法逾越的边界,因为它们只能在平面上移动,无法从上方跨越这个圆形 。而在三维空间中,我们可以轻松地从圆形的上方拿起一个物体,然后放到圆形的另一侧,这在二维生物看来,就像是物体突然消失又突然出现,完全超出了它们的认知范围 。

同样地,在四维空间中,一个三维物体的内部结构对于四维生物来说可能是完全暴露的,就像我们可以清楚地看到二维平面上的图形一样 。四维生物可以轻松地进入三维物体的内部,而不需要穿过它的表面,这在我们三维生物看来,同样是不可思议的 。
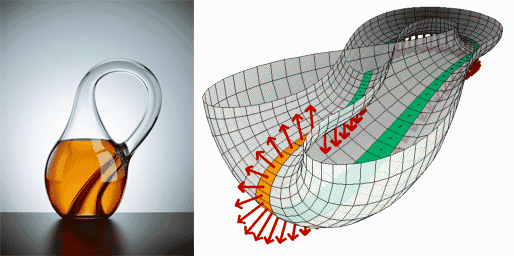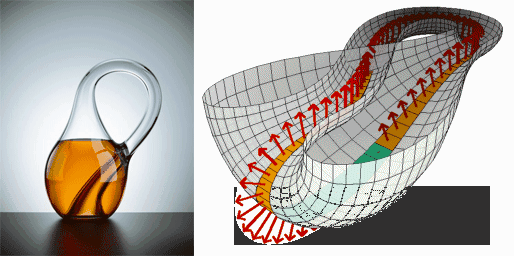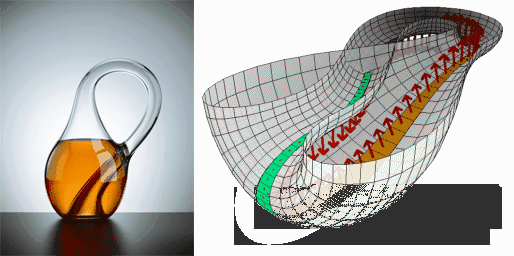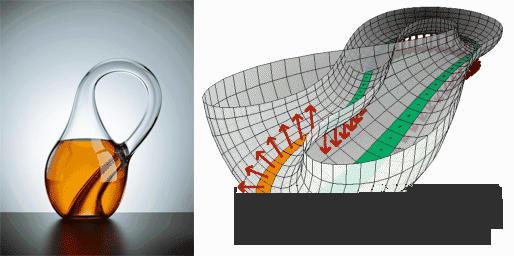
为了帮助人们想象四维空间,科学家们提出了一些思想实验和模型,其中最著名的就是莫比乌斯环和克莱因瓶 。莫比乌斯环是一种只有一个面和一条边界的曲面,它展示了在二维空间上可以实现向任何方向运动最终都可以回到原点的性质 。

我们可以将一张纸条扭转 180 度后首尾相连,就得到了一个莫比乌斯环 。在这个环上,一只蚂蚁可以沿着它的表面一直爬行,不需要越过边界就可以到达纸条的另一面,而且最终会回到原点 。莫比乌斯环的存在,让我们感受到了维度的奇妙之处,也为我们理解四维空间提供了一个小小的启示 。
克莱因瓶则是一个更为奇特的模型,它被认为是一种象征着四维空间的物体 。克莱因瓶没有内外之分,它的瓶颈延伸并扭曲地进入瓶子内部,与底部的洞相连,形成了一个封闭的曲面 。在三维空间中,我们无法制作出真正的克莱因瓶,因为它需要借助第四维度才能实现这种奇特的结构 。但我们可以通过想象和数学模型来理解它的特性 。

在克莱因瓶中,物体可以在不打破表面的情况下,从内部到达外部,或者从外部到达内部,这体现了四维空间中空间的连续性和无边界性 。虽然克莱因瓶仍然只是在三维空间思维框架内对四维空间的有限模拟,但它为我们打开了一扇通往四维空间想象的大门 。
由于多出一个维度,四维空间在规模和包容性上可能远超三维空间 。这就好比在二维平面上摆满物品后,若想继续增加物品,就需要向第三维度拓展,将物品堆叠起来,从而形成三维空间。同理,四维空间能够容纳更多的物质和信息 。在三维空间中,我们可以构建一个巨大的仓库来存放各种物品,但仓库的容量终究是有限的。
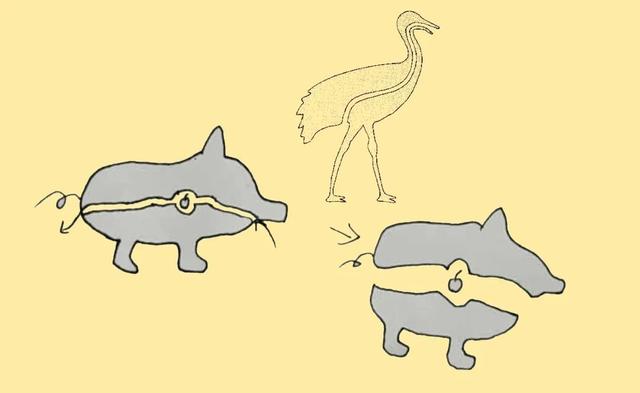
而在四维空间中,这个仓库的容量将得到极大的扩展,能够容纳更多种类和数量的物品 。从宇宙的角度来看,四维空间的存在或许能够解释一些关于宇宙物质分布和结构的谜题。如果宇宙中存在四维空间,那么其中的物质分布可能更加复杂和多样化,不同维度的空间可能相互交织、相互影响,共同塑造了宇宙的宏观结构 。
在四维空间中,物体的运动方式和路径选择将比三维空间更加多样化 。在二维空间中,物体只能在平面上沿着两个方向移动,从一个点到另一个点的路径相对单一 。当我们将视角提升到三维空间时,物体不仅可以在平面上移动,还可以在垂直方向上运动,从一个点到另一个点的路径选择变得更加丰富 。在三维空间中,一架飞机从一个城市飞往另一个城市,可以选择不同的航线,高度和速度也可以根据实际情况进行调整 。
而在四维空间中,物体从一个点到另一个点的路径选择将呈指数级增长,甚至可能实现类似瞬间移动的效果 。这是因为四维空间中的物体具有更多的自由度,它可以在额外的维度上进行移动,从而绕过三维空间中的障碍物,实现更快捷的移动 。
想象一下,在三维空间中,我们要从一个房间的一角走到另一角,需要沿着墙壁和地面行走,可能会遇到家具等障碍物 。但在四维空间中,我们可以直接穿过这些障碍物,瞬间到达目的地 。这种运动方式的差异,将对物体的动力学和运动规律产生深远的影响 。
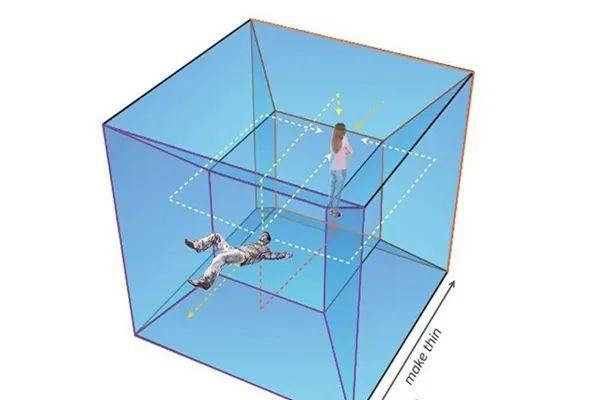
在四维空间中,对三维空间进行折叠和操纵可能成为现实 。我们可以通过类比在三维空间中折叠二维纸张的行为来理解这一概念 。当我们将一张二维纸张折叠时,原本在纸张上相距较远的两个点,通过折叠可以变得非常接近甚至重合 。在四维空间中,生物或许能够轻易地对三维空间进行类似的折叠操作,从而实现远距离的跨越 。

这种空间的折叠和操纵可能为时间旅行等概念提供了理论基础 。如果能够将三维空间折叠,使得不同时间点的空间位置重合,那么就有可能实现时间旅行 。
尽管目前这只是一种大胆的猜想,但它激发了科学家们的深入思考和研究 。如果人类能够掌握四维空间中空间折叠和操纵的技术,那么我们将能够突破时空的限制,实现星际旅行,探索宇宙的更深奥秘 。但这也带来了一系列的伦理和科学问题,比如时间旅行可能引发的因果律冲突等,这些问题都需要我们在未来的研究中进一步探讨和解决 。
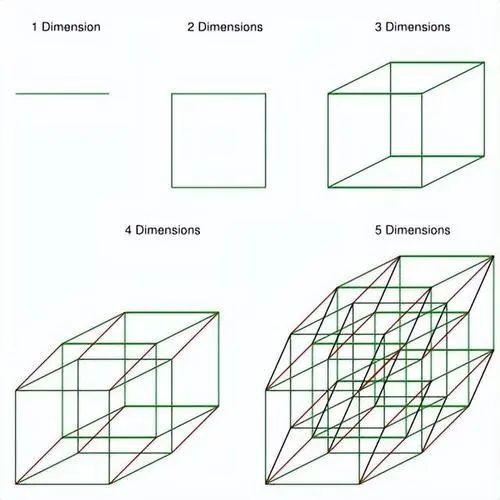
三维空间是我们生活的现实世界,由长、宽、高三个维度构成,物体的位置和形态可以通过三个坐标来描述 ,我们能够直观地感知和理解这个空间中的一切。而四维空间则是一个更为抽象的概念,在数学和物理学中被广泛探讨。它在三维空间的基础上增加了一个维度,无论是数学上的第四个坐标轴,还是物理学中与空间紧密结合的时间维度,都使得四维空间超越了我们日常的感知和想象 。
从数学视角看,四维空间的坐标系和空间形态与三维空间有着显著的区别,其复杂性和抽象性让我们难以直观把握;从物理视角看,四维时空的统一以及物理规律在四维空间中的变化,为我们揭示了宇宙更为深刻的奥秘 。