
反复试验的方法通常有助于解决此类问题。但这次不行!
这是四个不同颜色的圆圈,排列成 2x2 的网格。第一行的圆圈加起来是 9,第二行的圆圈加起来是 7。
类似地,第一列中圆的乘积为 36,第二列中圆的差为 11。
挑战在于:哪些数字适合这些圆圈?
提示:为每个圆圈分配变量。
拿起笔和纸,开始解这个谜题吧。如果你答对了,那就击掌庆祝吧!你是个数学明星,但请继续关注,看看我们的方法是否匹配。如果你答错了,别着急,跟着我一起做吧!
你准备好了吗?让我们开始吧!
首先,让我们给每个圆圈贴上标签。
设黄色为y,绿色为g,粉色为p,蓝色为b

这样,我们就可以形成一个方程组。

诀窍就在这里!如果我们得到其中一个变量,那么得到其他变量就会更容易。例如,如果我们得到p ,我们可以从方程 (iv) 得到y,从方程 (ii) 得到b。如果我们得到y,我们也可以从方程 (i) 得到g。
让我们看看如何获得p
为了做到这一点,我们将使用方程 (iv)、(i) 和 (ii)。
这里的目标是得出一个只有一个变量的方程——p
从 (iv) 开始,y = 36/p
让我们用这个值代替方程(i)

从这里开始,g = 9–36/p
如果我们在方程(iii)中替换这个值,它就变成

此时,我们有两个变量。我们可以消除b吗?当然可以!让我们用给出 p 的表达式替换它。
再看一下方程组。只有方程 (ii) 有变量b和p。
因此,根据公式 (ii),b = 7-p
我们继续进行替换吧!
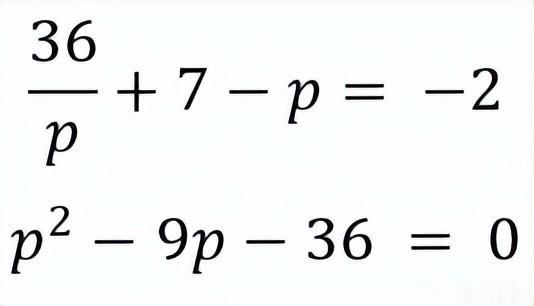
好了!我们现在有一个仅包含变量p 的表达式。
解这个二次方程,我们发现 p 要么是12,要么是-3
这意味着两组数字可以使该系统有效。
条件是p为 12 和 -3 时。
以下是p为 12(左)和 p 为 -3(右)时的值

非常感谢你的阅读!希望你喜欢这个谜题。