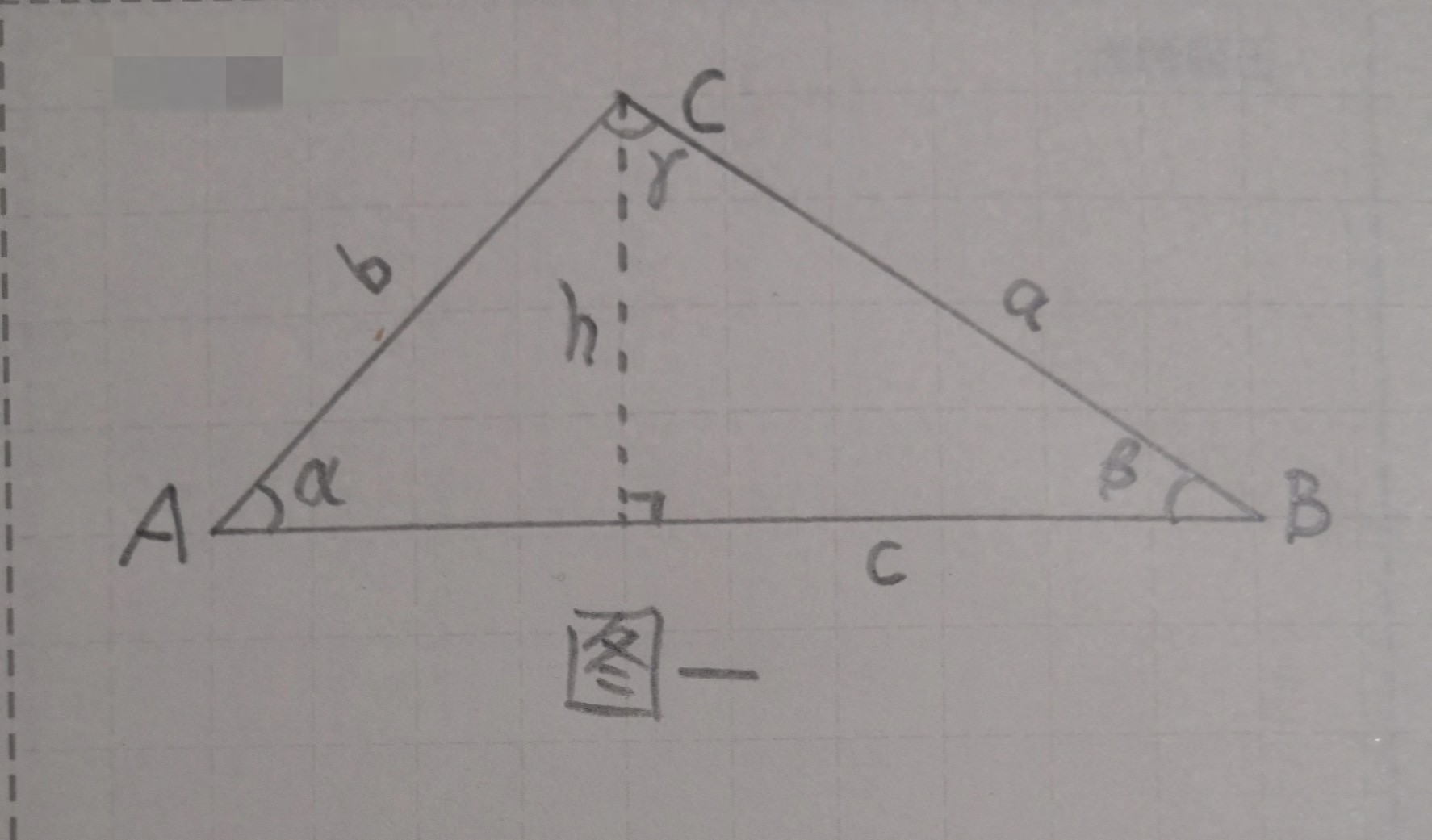
图一

考虑任意一个三角形ABC(见图一)，从点C作AB的垂线h，边a、b在h上的投影(不妨称为垂直投影)必然相等，因此：

asinβ=bsinα......(1)

或a:sinα=b:sinβ。对b、c两边重复这个过程，可得

b:sinβ=c:sinγ

因此，a:sinα=b:sinβ=c:sinγ=2R

这就是正弦定理。

另一方面，a、b两边在AB上的投影(水平投影)之和一定等于线段AB的长度(即c)，因此，我们得到：

c=acosβ+bcosα......(2)

通过循环置换，可以写出射影定理的3个公式：

a=bcosγ+ccosβ......(2.1)

b=acosγ+ccosα......(2.2)

由公式(2)马上得到：

c≤a+b......(3)

当且仅当α=β=0°时等号成立。这就是著名的三角不等式。

由于公式(2)包含两角三边共5个变量，所以用来解三角形的用途受限。但是，我们可以同时利用公式(1)和公式(2)，以此来减少变量的个数。

对公式(2)的两边同时平方，可以得到

c²=a²cos²β+b²cos²α+2abcosαcosβ

=a²(1-sin²β)+b²(1-sin²α)

+2abcosαcosβ

=a²+b²-(asinβ)(asinβ)-(bsinα)(bsinα)+2abcosαcosβ

利用公式(1)，可以将此式写成：

c²=a²+b²-(asinβ(bsinα)-

(asinβ)(bsinα)+2abcosαcosβ

=a²+b²+2ab(cosαcosβ-sinαsinβ)

=a²+b²+2abcos(α+β)

由于

cos(α+β)=cos(180°-γ)=-cosγ

因此可得

c²=a²+b²-2abcosγ......(4)

这正是我们所熟知的余弦定理。

因此，三角形的三个定理只是如下结论的一个简单表示：

在三角形中，从任一顶点到其对边所作的高是其邻边的垂直投影，而其对边长是其邻边的水平投影之和。

以上内容引自《三角之美：边边角角的趣事》，[以色列]伊莱·马奥尔 著，曹雪林 边晓娜 译，人民邮电出版社2018年12月

最后，我们解一道高考题作为本文的结束。

题目呈现：(2000年北京春季高考题)

在△ABC中，角A、B、C的对边分别为a、b、c.求证：

(a²-b²):c²=sin(A-B):sinC.

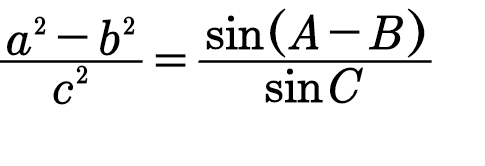
解题思路：本题是一道综合题。先用余弦定理的两式相减，再用正弦定理代入，最后用四大天王公式完成证明，过程比较简洁。

证明：由余弦定理，知

a²=b²+c²-2bccosA，

b²=a²+c²-2abcosB.

两式相减，得

a²-b²=b²-a²-2bccosA+2accosB

a²-b²+a²-b²=2c(acosB-bcosA)

2(a²-b²)=2c(acosB-bcosA)

a²-b²=c(acosB-bcosA)

两边同时除以c²得

证明过程用到了正余弦定理和四大天王公式。

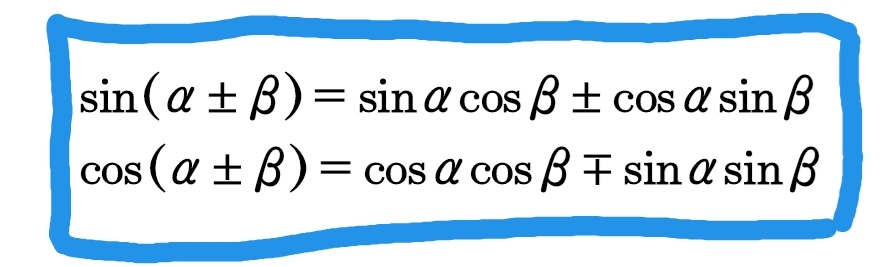
四大天王公式

科学尚未普及，媒体还需努力。感谢阅读，再见。