你是否曾想过，数学这座看似坚不可摧的大厦，也曾险些因为一个关于“理发师该不该给自己刮脸”的问题而轰然倒塌？这听起来可能有些不可思议，但正是这个简单悖论，在20世纪初的数学界引发了一场大地震，史称“第三次数学危机”。本文将用通俗易懂的语言，带你了解这段波澜壮阔的数学历史。

1 集合论的诞生：从无穷说起

要理解第三次数学危机，我们首先得认识一位关键人物：德国数学家格奥尔格·康托尔。在19世纪70年代，康托尔做了一件当时看来非常“叛逆”的事情——他开始系统研究“无穷”这个概念。

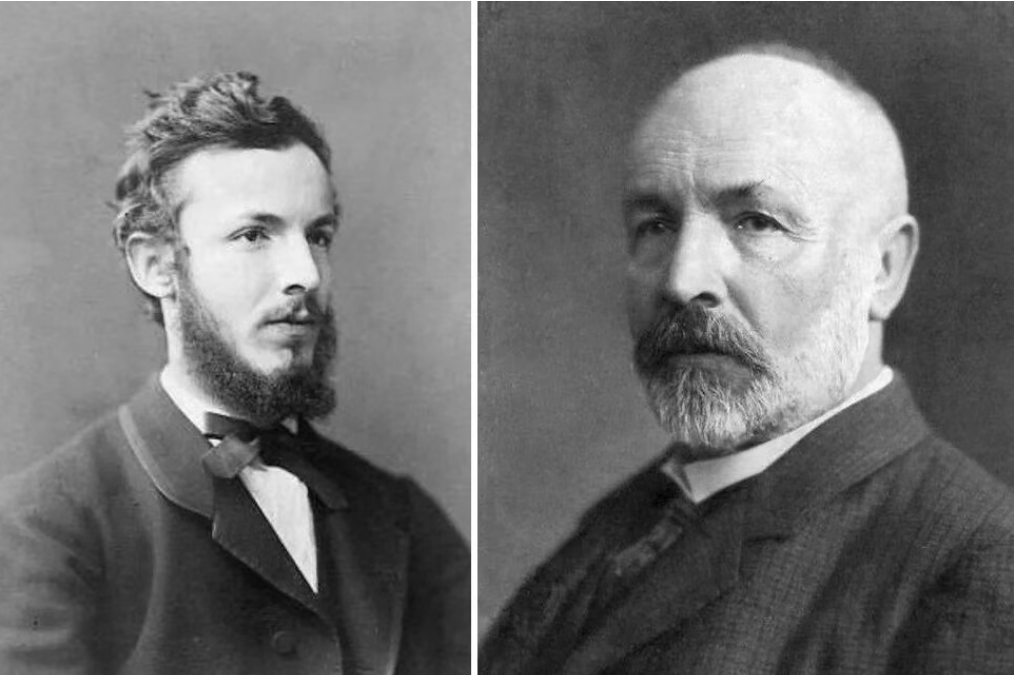
在我们日常生活中，谈论的都是有限的事物：5个苹果、100个人、1万本书。但“无穷”则完全不同，它代表着没有尽头。在康托尔之前，数学家们对“无穷”大多敬而远之，认为这是一个说不清道不明的概念。

康托尔的革命性想法是：即使面对无穷，我们也可以比较大小。他是怎么做的呢？通过“一一对应”的原理。想象一下，有一个电影院，我们要判断座位数和观众数是否相等。最简单的方法就是看是否每个座位都坐了一个人，且没有站着的人。如果有观众站着，那就说明观众比座位多；如果有空座位，那就说明座位比观众多。

康托尔将这一思想用在了无穷集合上。令他惊讶的是，他发现并非所有的无穷都一样大。比如，自然数（1, 2, 3, 4...）有无穷多个，实数（包括整数、分数和无理数如π）也有无穷多个，但实数的“无穷”却比自然数的“无穷”大得多！这意味着无穷也是分层次的。

基于这些研究，康托尔创立了集合论。简单来说，集合就是把一些确定的、不同的东西放在一起形成的整体。比如，一个班级的所有学生可以形成一个集合，所有自然数可以形成一个集合。集合论提供了描述和处理数学对象的统一语言，到19世纪末，数学家们发现几乎所有的数学都可以建立在集合论的基础上。法国著名数学家庞加莱（没错，就是那位代数拓扑学奠基人）甚至自豪地宣布：“借助集合论概念，我们可以建造整个数学大厦……我们可以说绝对的严格性已经达到了。”

然而，康托尔的工作也遭到了同时代一些权威数学家的强烈反对，比如利奥波德·克罗内克就曾激烈批评他的理论。在巨大的精神压力下，康托尔一度患上精神分裂症，最终于1918年在哈雷的一家精神病院逝世。

2 数学大厦的裂缝：悖论的出现

就在数学家们为数学基础的稳固而欢欣鼓舞时，危机却不期而至。一系列奇怪的“悖论”开始出现在集合论中，其中最具冲击力的是英国哲学家兼数学家伯特兰·罗素在1902年提出的悖论。

2.1 罗素悖论与理发师悖论

罗素构造了这样一个集合：所有不包含自身的集合组成的集合。这听起来有点绕，我们用一个更通俗的比喻——“理发师悖论”来解释。

某个村庄有一位理发师，他宣布了一条规则：我只给而且专门给村里所有不给自己刮胡子的人刮胡子。

那么问题来了：这位理发师该不该给自己刮胡子？

如果他给自己刮胡子，那么他就属于“给自己刮胡子的人”。根据他的规则，他就不应该给自己刮胡子。

如果他不给自己刮胡子，那么他就属于“不给自己刮胡子的人”。根据他的规则，他就应该给自己刮胡子。

无论哪种情况，都会导致矛盾。这就好比说“这句话是假的”——如果这句话是真的，那么它说的是真的，但内容却说自己是假的；如果它是假的，那么它说自己假又是真的了。

罗素将这个悖论转化为了集合论语言：设集合R是由所有不包含自身的集合组成的集合。那么R是否包含自身？

如果R包含R自身，那么根据R的定义（R只包含那些不包含自身的集合），R就不应该包含R。

如果R不包含R自身，那么根据R的定义，R又应该包含R。

无论哪种情况都自相矛盾。这个悖论的可怕之处在于，它只使用了集合论中最基本的概念——集合、元素和属于关系，没有任何高深复杂的知识。

2.2 危机爆发：数学基础的动摇

罗素悖论的发现给数学界带来了巨大冲击。当时德国逻辑学家弗雷格正准备出版《算术的基本法则》第二卷，他在收到罗素的信后，在书中无奈地写道：“一位科学家不会碰到比这更难堪的事情了，即在工作完成之时，它的基础垮掉了。”

为什么一个看似简单的悖论会引起如此大的恐慌？因为集合论已经被公认为整个数学的基础。几何学、代数、微积分等数学分支都可以从集合论推导出来。这就好比一栋大楼的地基被发现有一条裂缝——即使裂缝看起来不大，但所有人都担心它会导致整栋大楼倒塌。

实际上，在罗素之前就已经有悖论被发现。1897年，布拉里·福蒂揭示了第一个集合论悖论。1899年，康托尔本人也发现了类似的悖论。但当时数学家们认为这些只是技术性问题，可以通过小修小补来解决。罗素悖论则不同，它直击集合论的核心概念，无法被轻易忽略。

3 危机的解决：公理化集合论

面对危机，数学家们开始寻求解决方案。他们的目标很明确：对集合论进行改造，使其既能保留原有有价值的内容，又能排除悖论。这就像修改宪法一样，需要确立一些基本规则（公理），明确规定什么样的对象才能被称为集合，以及集合可以有哪些操作。

3.1 ZF/C公理系统

1908年，德国数学家策梅洛提出了第一个集合论公理系统，后来经弗兰克尔等人的改进，形成了现在广泛使用的ZF公理系统（策梅洛-弗兰克尔公理系统）。如果再加入选择公理，就称为ZFC公理系统。

这个系统的核心思想是：不是任何对象的汇集都能被称为集合。通过一系列精心设计的公理，我们可以限制集合的构造方式，避免出现“所有集合的集合”这种过于庞大而导致矛盾的汇集。

举个例子，ZF系统中的一个重要公理是分离公理模式：给定一个集合和一条性质，我们可以从该集合中分离出那些满足该性质的元素，组成一个新的集合。这意味着我们不能凭空构造一个“所有不包含自身的集合的集合”，而只能从某个已知集合中分离出元素。

这就像父母给孩子一盒积木时说：“你可以用这些积木盖房子，但不能用其他材料”。这样，孩子就不会造出太大太危险的结构。ZF/C公理系统就好比给集合的构造制定了安全规范，防止建造出问题集合。

3.2 悖论的避免

通过这种公理化方法，罗素悖论被成功避免了。因为在这种公理系统下，我们根本无法构造出“所有不包含自身的集合的集合”这样的对象——它根本不被承认是一个合法的集合。

这就好比解决了理发师悖论：只要修改规则，说明“本规则不适用于理发师本人”，矛盾就消失了。当然，实际的数学处理要比这严谨得多，但基本思路类似——通过限制集合的构造规则来避免自指矛盾。

到20世纪中叶，ZF/C公理系统已被广泛接受为集合论的基础，也为整个数学提供了一个相对可靠的基础。第三次数学危机就此得到缓解。

4 危机的深远影响

第三次数学危机虽然通过公理化集合论得到了解决，但它对数学的深远影响却持续至今。

促进数学基础研究：危机促使数学家们更加深入地研究数学基础问题，催生了数理逻辑等新学科。围绕数学基础之争，形成了三大数学哲学流派：逻辑主义（认为数学是逻辑的延伸）、直觉主义（强调数学构造性）和形式主义（主张数学是符号游戏）。

奠定现代数学范式：公理化集合论的成功，确立了公理化方法在现代数学中的核心地位。如今，大多数数学分支都建立在 ZFC 公理系统之上，以公理为起点进行严谨推导。

推动计算机科学的发展：为解决危机而产生的数理逻辑，为计算机科学奠定了理论基础。图灵、哥德尔等人的工作直接受益于对数学基础的深入探讨。罗素悖论中使用的对角线法，后来被图灵用于解决停机问题，被哥德尔用于证明不完备定理。

认识数学的本质：第三次危机让人们认识到，数学并非绝对真理的化身，而是不断发展的学科。正如一位数学家所说：“完美的数学并不存在，人们不必为它的瑕疵而伤心，反而应该为它无限的可能性而欢欣。”

值得一提的是，1931年哥德尔提出的不完备定理表明，任何一个足够强大的公理系统（如ZFC系统）都无法同时满足完备性和一致性。这意味著数学中总存在一些既不能被证明也不能被否定的命题。这可以看作是第三次数学危机的余波，它揭示了数学固有的局限性。

回顾集合论和第三次数学危机的历程，我们可以看到数学发展的典型模式：提出新理论 → 发现矛盾 → 修正理论 → 更深层次的发展。这种循环不是简单的重复，而是数学不断自我完善、向更高层次迈进的过程。

康托尔开创的集合论为数学提供了统一基础，罗素悖论揭示了这一基础的潜在问题，而ZF/C公理系统则通过公理化方法为数学建立了相对可靠的基础。这一过程不仅解决了危机本身，也极大地丰富了数学的内涵，促进了20世纪数学的蓬勃发展。

今天的数学大厦或许已经比一个世纪前更加稳固，但数学的基础问题依然吸引着数学家们的思考。也许正如希尔伯特所说：“我们必须知道，我们必将知道。”——对数学真理的追求，本身就是一个永恒的过程。