两角和差的三角函数关系式在解某些综合题时，也常常起到重要的作用。

我们来解一道三角函数计算题。题目呈现：设cos32°=0.848，不查表计算sin46°的值(精确到0.01)。

分析：考虑到46°=30°+16°，而16°是32°的一半，故可由半角公式求出sin16°和cos16°，再用正弦两角和差角公式计算sin46°。半角公式如下图所示：

解：先求sin16°和cos16°，过程如下图所示：

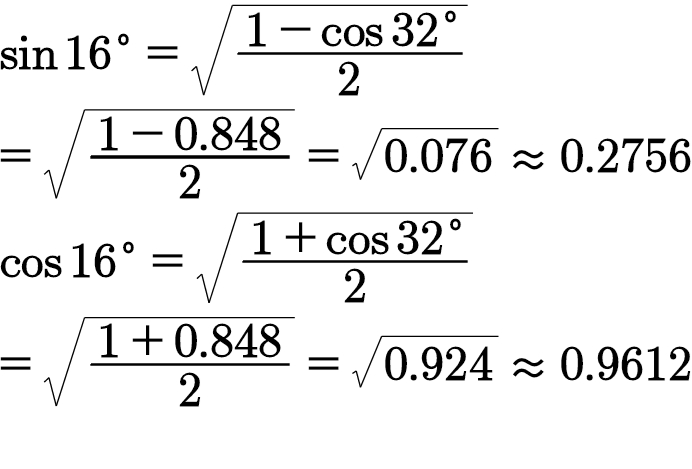
因为16°在第一象限，故根号前取正号。

sin46°=sin(30°+16°)

=sin30°cos16°+cos30°sin16°

=0.5×0.9612+0.8660×0.2756

=0.4806+0.2387=0.7193≈0.72

计算过程有个难点，即笔算平方根。推荐阅读下面的我的往期文章：

https://m.toutiao.com/is/U9Qgb5D/ - 生活中的魔法数学：平方根的笔算 - 今日头条

https://m.toutiao.com/is/U9Qp88M/ - 乘方和开方的计算(帮你记得牢算得快，轻松脑算的全脑科学速算法) - 今日头条

假如这道题是选择题或填空题，则有另外一种解法。

我们考虑求sin1°和cos1°。怎么求呢？因为题目要求的函数值是近似值，所以有办法。请看下图：

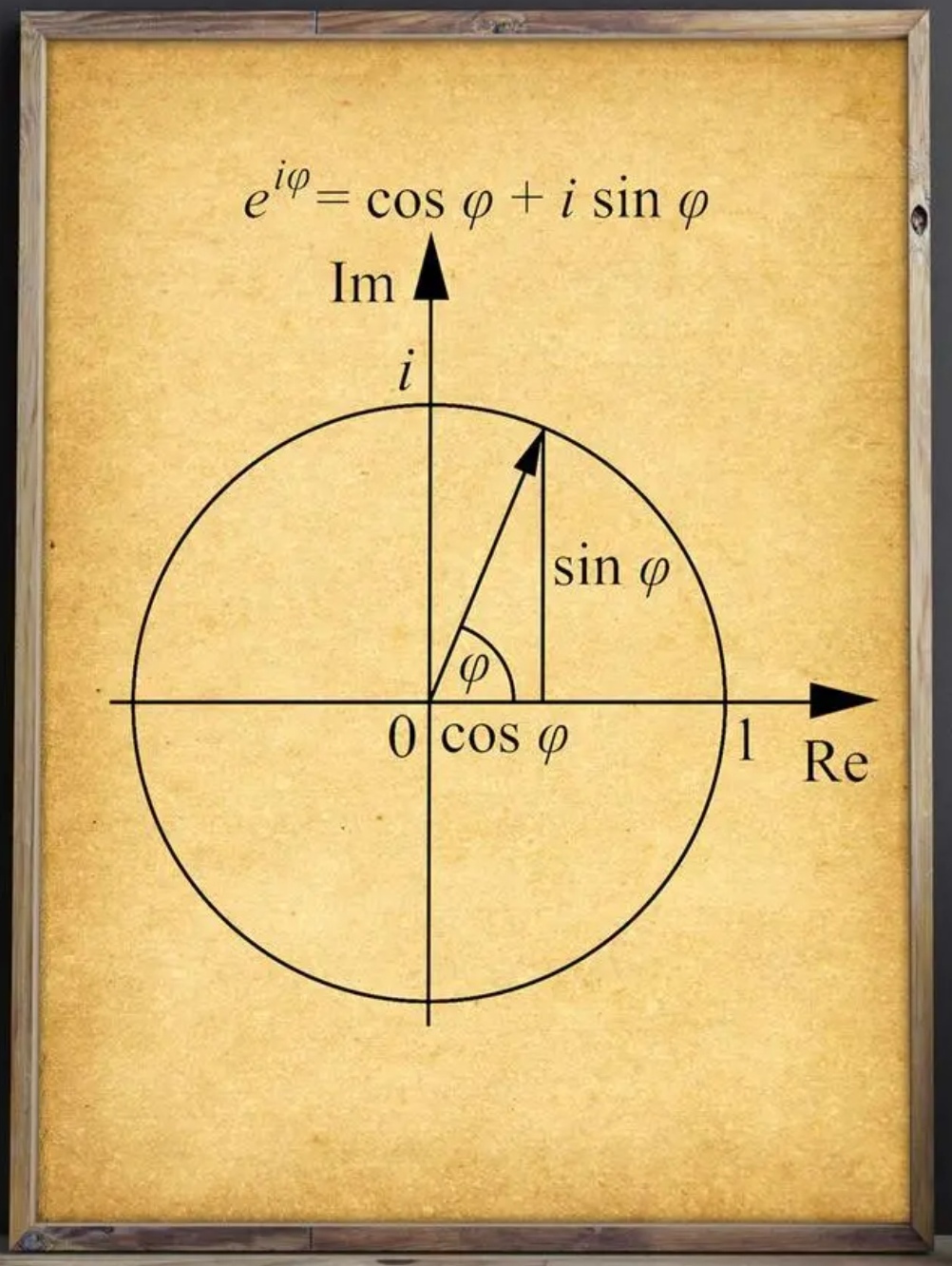
上面的图是复平面，x轴是实数，y轴是虚数。借用这张图是想说明欧拉用单位圆定义任意角的三角函数。

欧拉说过，sinα=函数线MP， 而cosα=函数线OP。MP和OP是图中直角三角形的两条直角边。如果角α的角度很小，可以近似处理为MP=角α所对的弧长。这样用曲线代替直线的做法，在角度很小时可以有足够的精度。

在单位圆中，圆心角1°角所对的弧长=2π÷360=π÷180

≈3.14159÷180=0.017453

约等于0.01745。

根据三角恒等式sin²α+cos²α=1，可得

cos1°≈0.99985

于是得到

sin46°=sin(45°+1°)

=sin45°cos1°+cos45°sin1°

=0.7071×0.99985+0.7071×0.01745=0.7070+0.01234

≈0.71934≈0.72

注意，这个解法没有用到已知条件cos32°=0.848，所以在合适的场合才能使用。

=0.4806+0.2387=0.7193≈0.72

中学数学用表请看下图：

科学尚未普及，媒体还需努力。感谢阅读，再见。