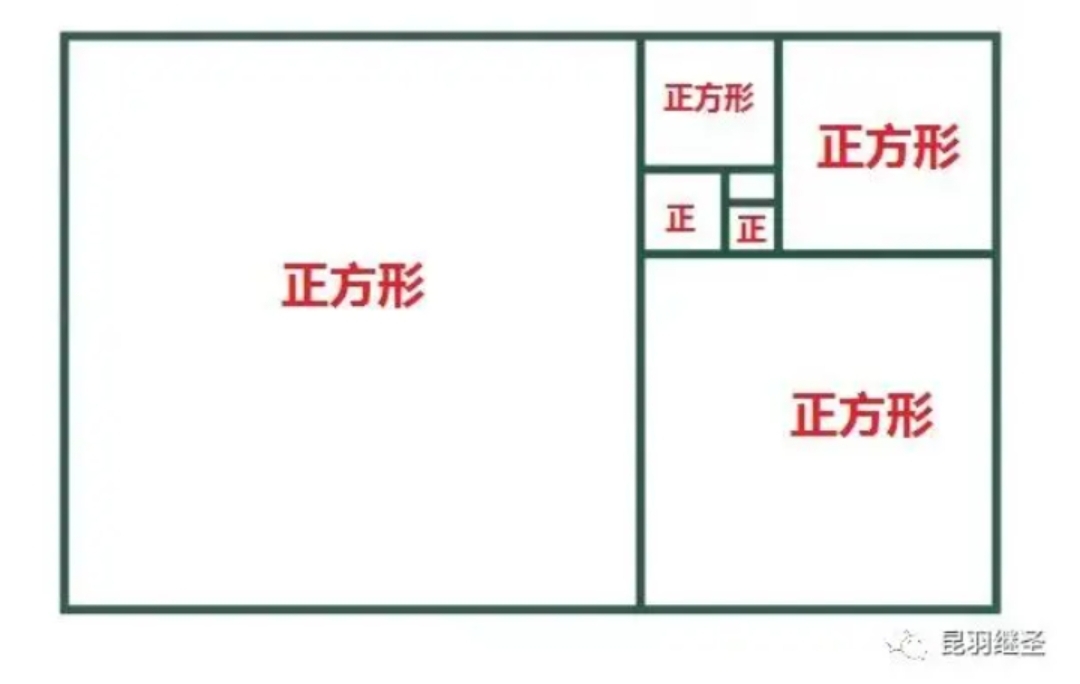
大正方形中有三个层层叠叠的正方形。

题目呈现如下：

重叠的正方形难题

题目取材于头条作者(几何魔法师辰辰)发布的作品。

我不想单纯地解题，而是借此契机谈谈对长方形的认识和对角线模型的建立。

长方形是常见的平凡的几何图形，它的面积公式非常简洁，即面积=长×宽。它的两条对角线互相平分。

长方形的对角线模型有几条有趣的结论。

对角线模型

连接长方形的一条对角线，并在对角线上任意选择一个点，例如点M，通过点M作两条十字交叉的平行线，把大长方形划分为四个小长方形，分别命名为S₁～S₄.

在上面的模型中，有以下结论：

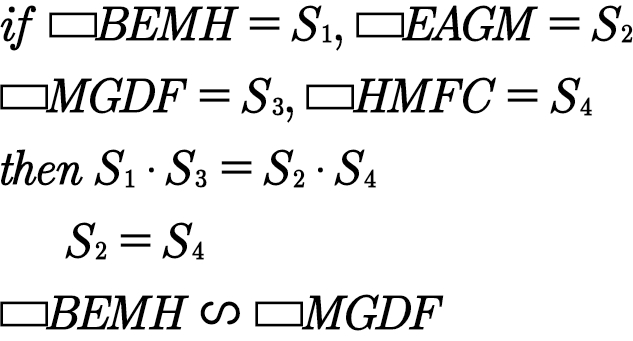
这三条结论让人产生类比联想，想到小学几何的蝴蝶模型。

长方形对角线模型的结论如何证明呢？当然是仁者无敌面积法了。等底长方形面积之比等于高之比，等高长方形面积之比等于底之比。这样就把面积之比转化为线段比了。

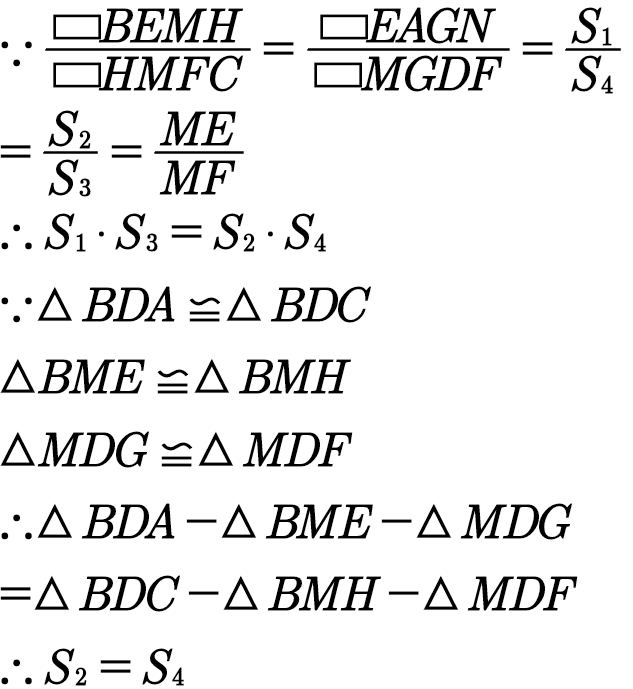
证明两个长方形相似太容易了，请大家看图自行证明。

S₁和S₃相似。

有人会问，如果十字交叉交点M不在对角线上会是什么情况?

请看下图：

虽然S₂和S₄不相等，S₁和S₃不相似，但是仍然有S₁·S₃=S₂·S₄成立。即20×12=15×16。

如上图所示，设S₂=20，S₃=40，求S₁和S₄，你能解答吗？

太简单了。相似长方形面积之比等于相似比的平方，所以S₁=10，S₄=S₂=20。

建立了以上共识，现在我们来解决正方形重叠难题。

把橙色正方形向左推到尽头，就是对角线模型中的S₂，我们知道S₂=S₄，又知道S₂+S₄=24，所以S₂=S₄=12。因为S₂·S₄=S₁·S₃，即12²=20S₁，所以S₁=144÷20=7.2。

故大正方形面积=20+24+7.2=51.2。

对角线模型的补充说明：

假如有人问你70英寸的平板电视平面面积为多少？你能解答吗？

70英寸指的是对角线长度，只需再确定电视的长宽比就能够计算屏幕面积了。

假定是16:9的平板电视，那么用勾股定理可以计算出两条直角边分别为9和16的直角三角形的斜边c的长度。再根据相似三角形对应线段成比例，可以计算出电视机的长和宽，也就得到电视机屏幕的面积了。

已知正方形的对角线长度=f，如何计算正方形的面积？

解：设正方形边长为a，则f=√2a，所以f²=(√2a)²=2a²，所以正方形面积S=a²=½f²。

科学尚未普及，媒体还需努力。感谢阅读，再见。