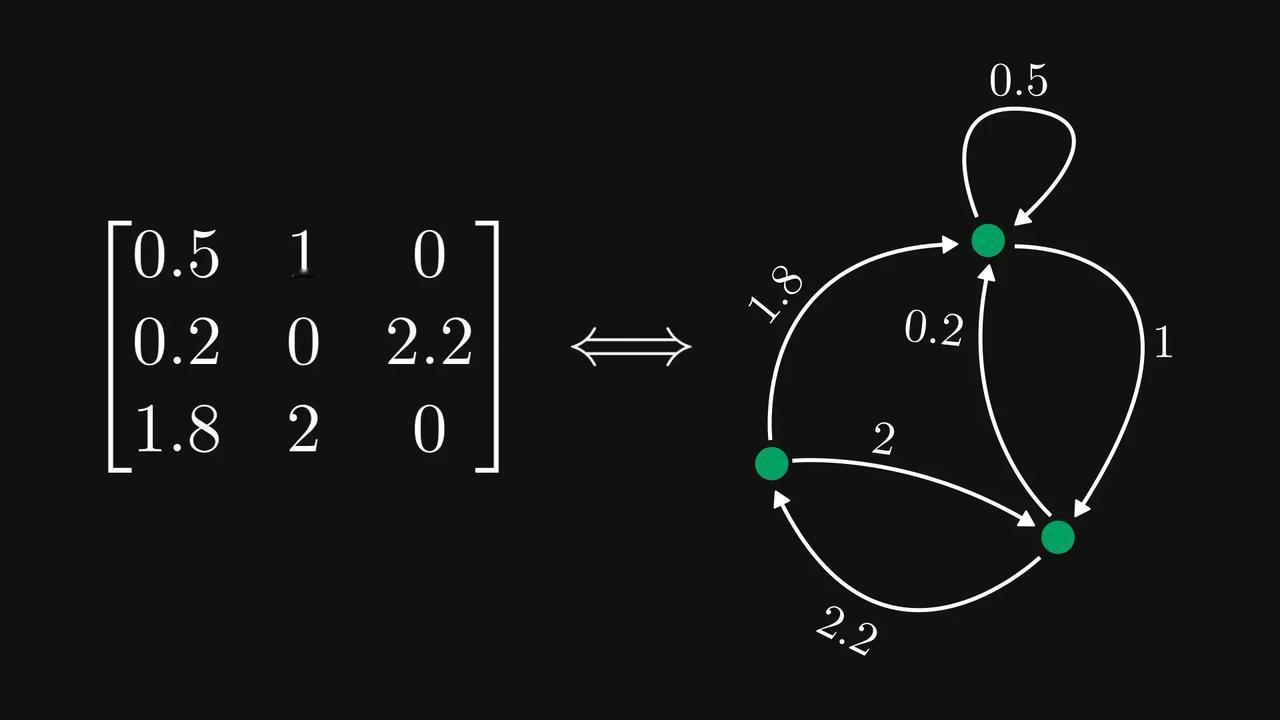
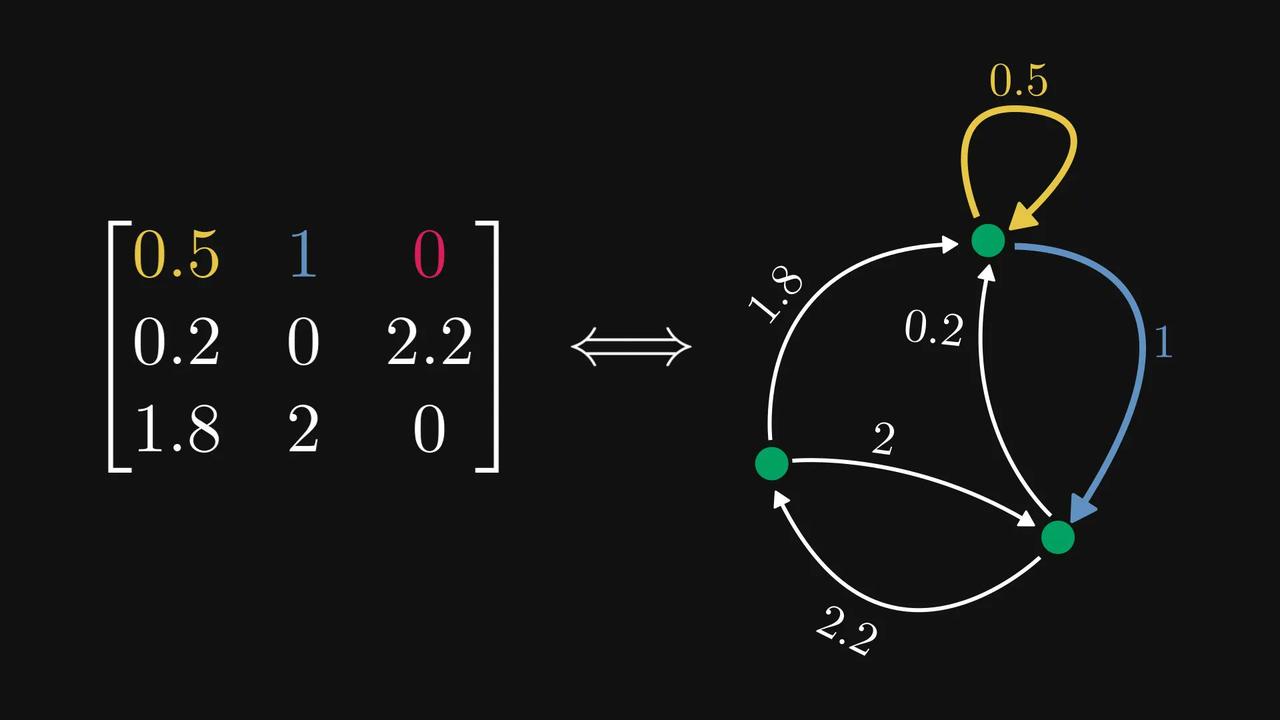
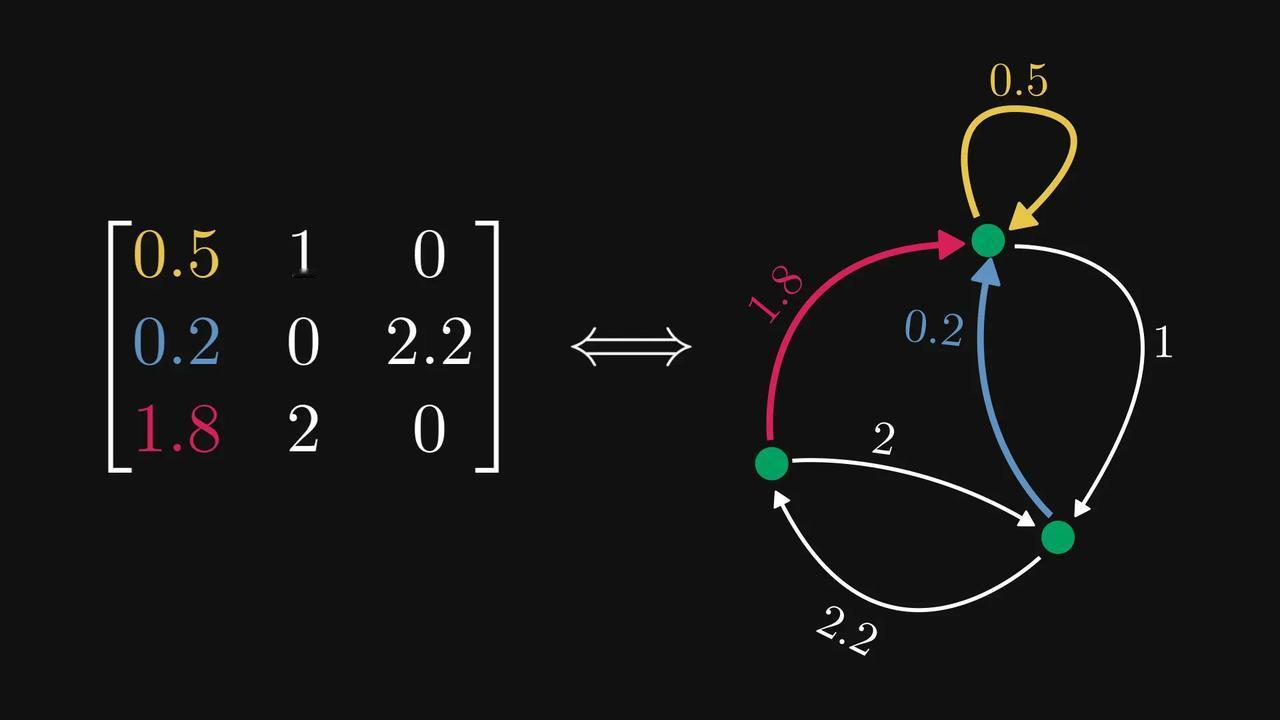
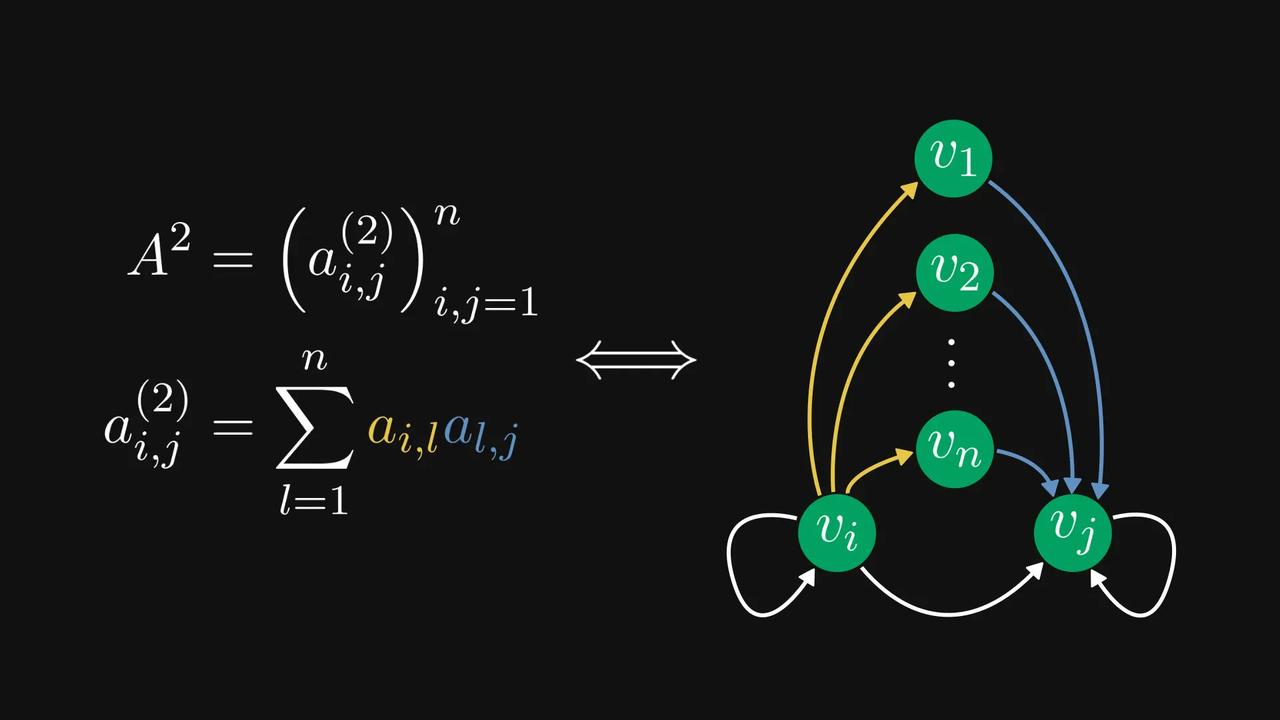
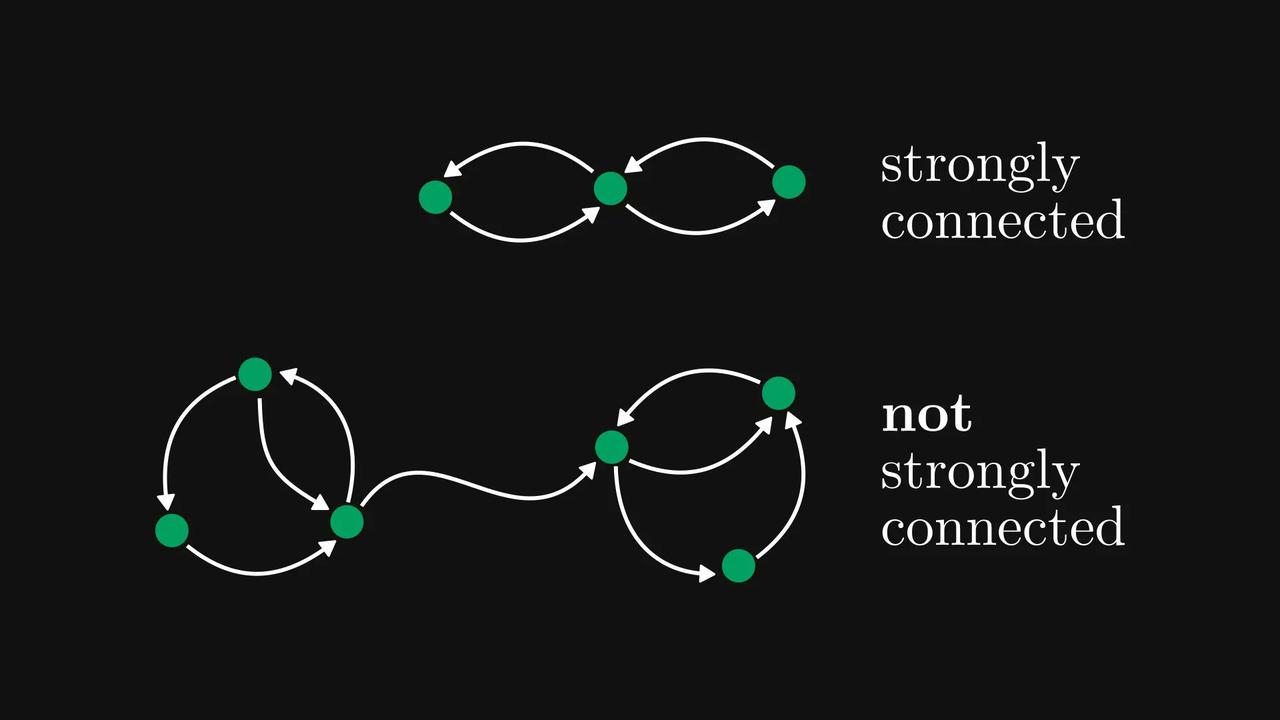
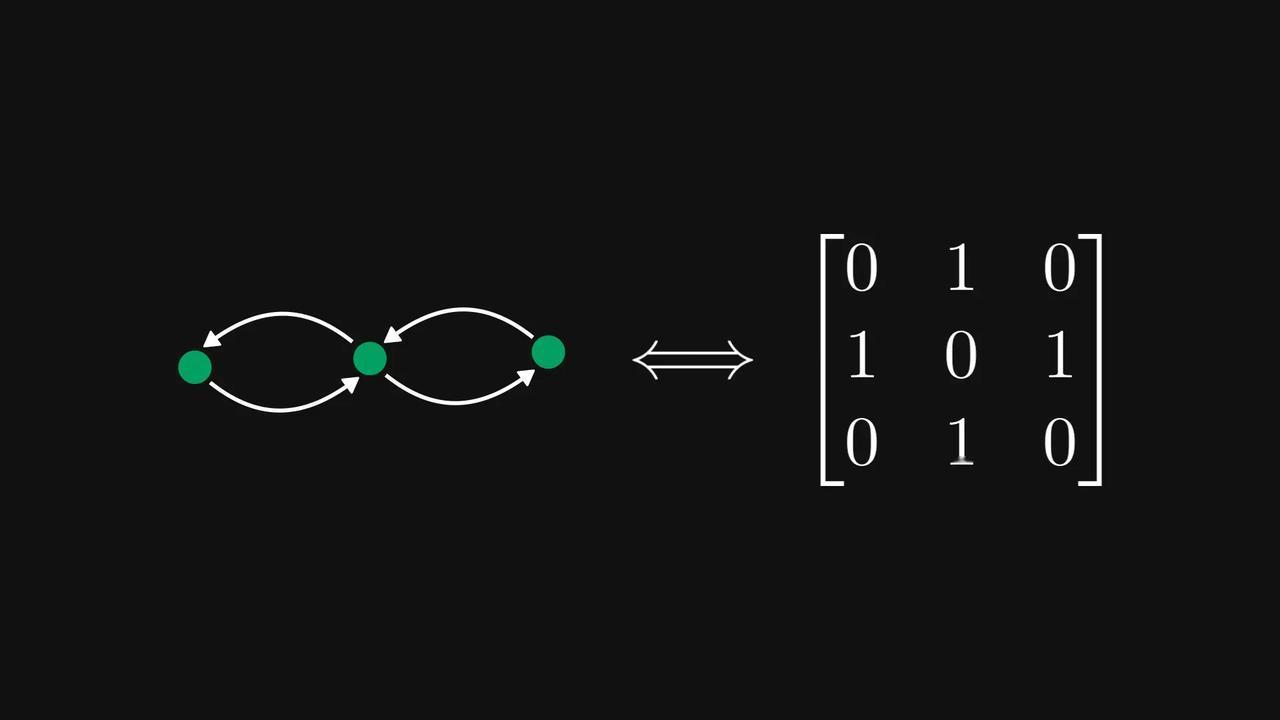
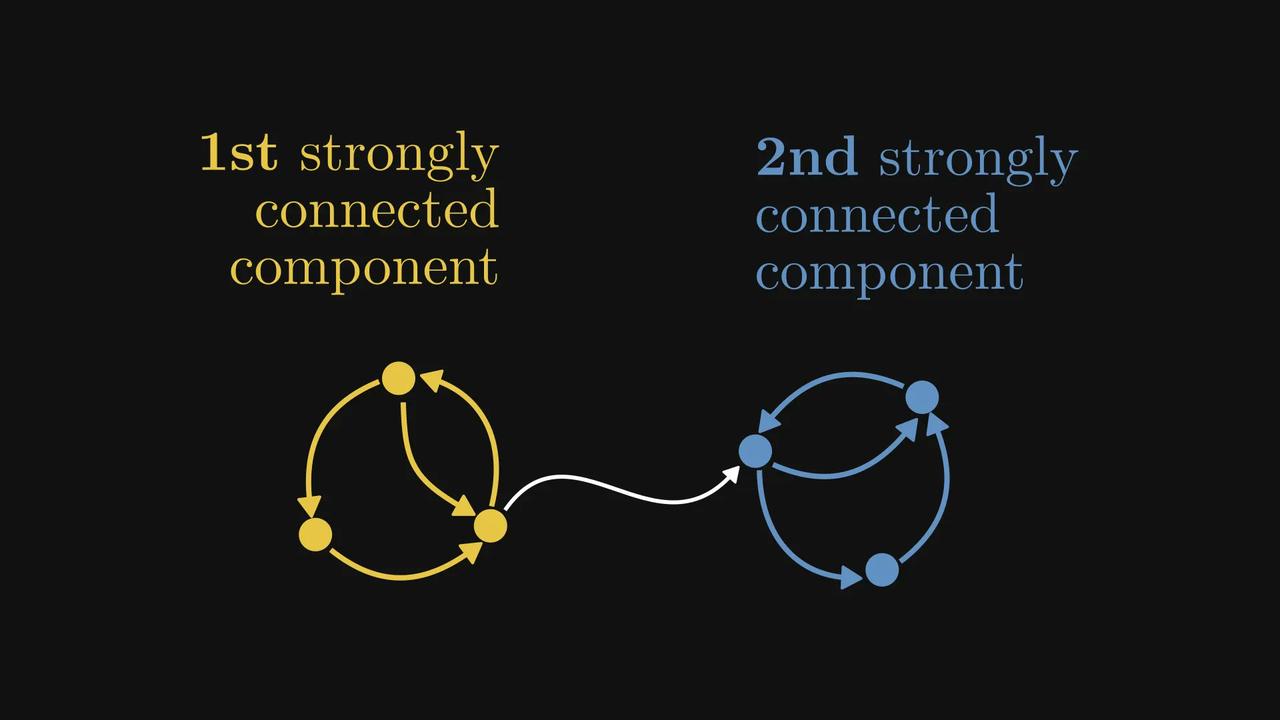
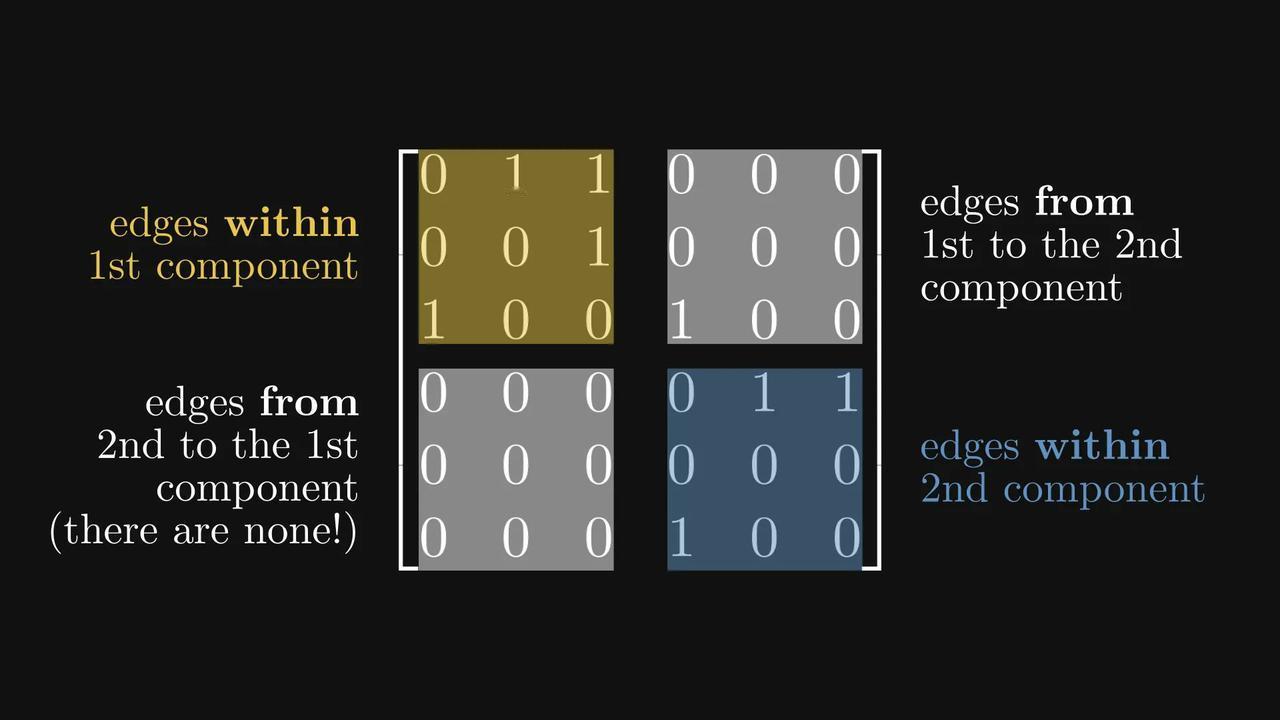
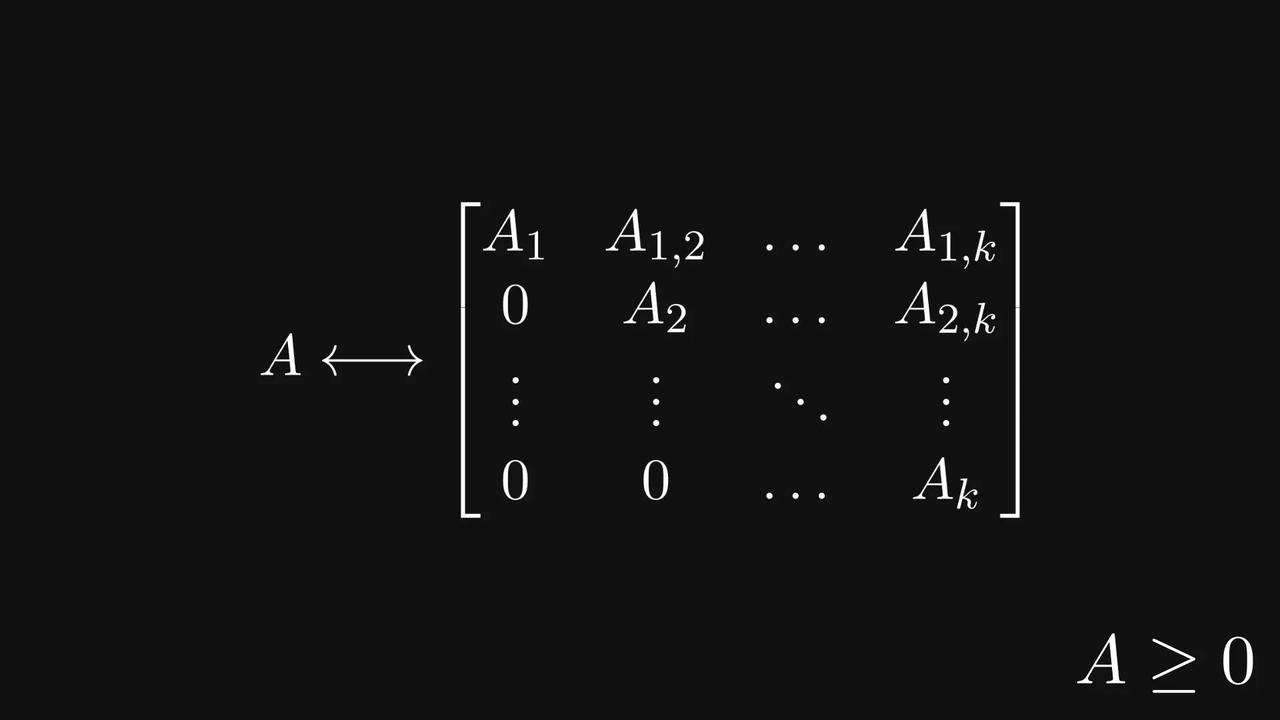#如何用图看懂矩阵##矩阵和图如何相互对应# 原来,非负矩阵可以被对应为一张张有向图? 数学科普作家Tivadar Danka为我们详细介绍了一下这个思路,先来看看这张酷似小乌龟的【图1】。 在【图1】中,每一行代表一个节点,每个元素代表一条带权重的有向边。数字为零的边会被自动忽略。 意思就是,第𝑖行第𝑗列的元素,将对应一条从节点𝑖指向节点𝑗的边。 看起来还是有点绕,我们直接看【图2】,假设第一行对应从最高处节点出发的边,那么(1,1) 处的元素就是一条指向自身的有向边。 以此类推,第一列就将是所有指向最高处节点的边。【图3】 这样的有向图有什么作用呢?我们再来看【图4】。 当你计算矩阵的平方(A²)时,实际上就是在统计图中所有可能的“连续两步走”路径组合。 矩阵的幂次运算直接对应着图中的路径。 如果把这张有向图想象成马尔可夫链的状态转移图,那么它的概率转移矩阵平方后,每个数字就代表了“经过两步转移后到达某个状态”的概率。 这样的思路,能将复杂的矩阵行为变得直观,利于我们研究。 现在我们再稍微延伸一下,来讨论强连通分量的概念。如果一个有向图的每个节点都可以从其他任何节点到达,我们称呼这个有向图为强连通的,反之则是非强连通的。【图5】 对应强连通图的矩阵称为不可约矩阵,其他非负矩阵称为可约矩阵。(为简单起见,假设每条边的权重为单位1,但权重可以是任意非负数。)【图6】 即使图不是强连通的,我们也可以将其节点划分为若干“强连通分量” 。【图7】 通过排列节点,可以将对应的矩阵转化为一种“超简洁”的结构——Frobenius标准形。【图8】 在这种形式下,主对角线上每个方块的图都是强连通的(即不可约的)。 反过来问:我们能否将任意非负矩阵转化为Frobenius标准形?可以,而且借助有向图,这比纯代数方法更容易证明。【图9】 矩阵与图之间的这种深刻联系,极大地促进了图论和线性代数这两个数学分支的发展。