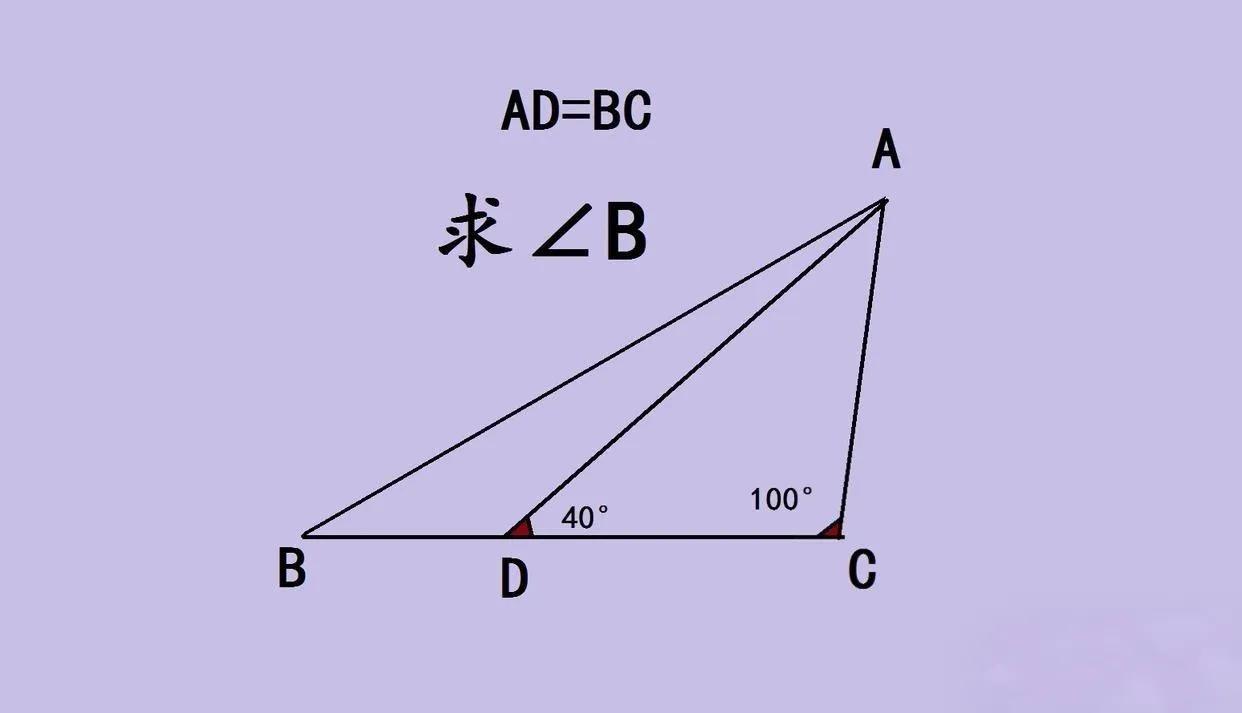
中考几何“全军覆没”题，藏着巧妙思路 这道中考几何压轴题，看着条件简单——AD = BC，求∠B度数，却让好多学生栽了跟头！ 图里的三角形，已知∠ADC = 40°，∠ACB = 100° ，关键要利用AD = BC这个条件找突破口。这类题很考验几何思维，得构造全等或等腰三角形，把分散条件串联。 好多同学一开始觉得条件少，实则要挖掘隐藏关系，比如作辅助线，让AD、BC关联起来。几何题的魅力就在这，看似“缺条件”，实则藏着逻辑链条，像拼图一样，找到关键一块，就能打通全盘。 中考里这种题，是区分度担当，能筛选出善于联想、构造的学生。做这类题，别慌，从已知条件出发，大胆尝试辅助线，把相等线段、角度关系盘活，答案自然浮现～ 你遇到过这种“看着简单实则烧脑”的几何题不，评论区聊聊解题崩溃瞬间！
评论列表
猜你喜欢
【1评论】【1点赞】
【4评论】【4点赞】
【3点赞】
【1评论】【7点赞】
作者最新文章
热门分类
艺林信步
作辅助线：在AD上取E，使DE=BD，连接BE，连接CE。作AG丄CE，作EF丄DC。则△AEC、△BDE为等腰三角形，RT△CEF为特殊三角形，EF=EG，RT△BEF≌RT△AEG，∴△ABD是等腰三角形，∠B=20+10=30。
艺林信步
这道几何题也许是我碰到的添附线最多的一题了！小有难度！共四条！
skynbcdf
猜测∠B=30°，所以以BC为边做正△BCE，连接AE，可证等腰△ACD≌△CAE，所以AC=AE，图形对称，∠EBA=∠CBA=30°。或者用圆周角定理，以AC为边做正△AOC，连接OB，同样易证等腰△ACD≌△BOC，所以OB=OC=OA，O为△ABC外心，所以∠B=30°