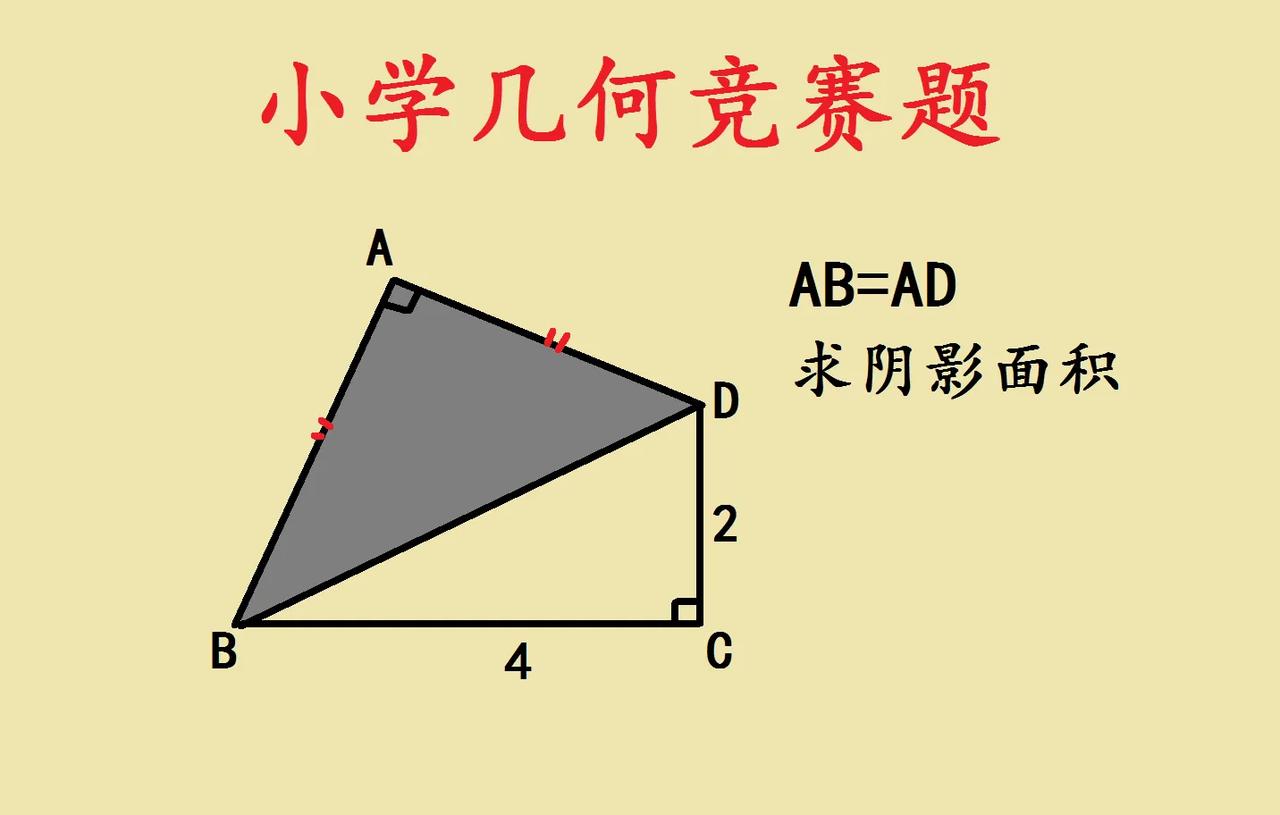
用旋转+赵爽弦图巧解小学几何题 家有小学生，遇到几何竞赛题别慌！今天用旋转和赵爽弦图思路，轻松解“阴影面积” 。 看题，已知 AB = AD ，图里有直角。咱可以把三角形 ABD 旋转 ，让 AB 与 AD 重合（因为 AB = AD ，旋转后能 “拼” 出新图形 ）。 想象一下，旋转后，结合赵爽弦图的思路，阴影部分和空白部分能组成规则图形。直角三角形 BCD 数据已知（底 4、高 2 ），但直接算阴影难。通过旋转，把分散的图形 “整合” ，利用 AB = AD 这个相等条件，让阴影面积和已知边长建立联系。 其实，旋转后阴影部分与其他部分构成的图形，能转化成我们熟悉的面积计算模型。借助赵爽弦图里 “图形重组、化不规则为规则” 的思想，不用复杂计算，就能发现阴影面积和直角三角形 BCD 等的关系，轻松求出结果～这种旋转 + 弦图的思路，超适合小学几何题，帮孩子打开解题新视角，遇到类似题再也不怕啦！
评论列表
猜你喜欢
【12评论】【1点赞】
【3评论】【12点赞】
【24评论】【36点赞】
作者最新文章
热门分类
轩辕羿雪
5