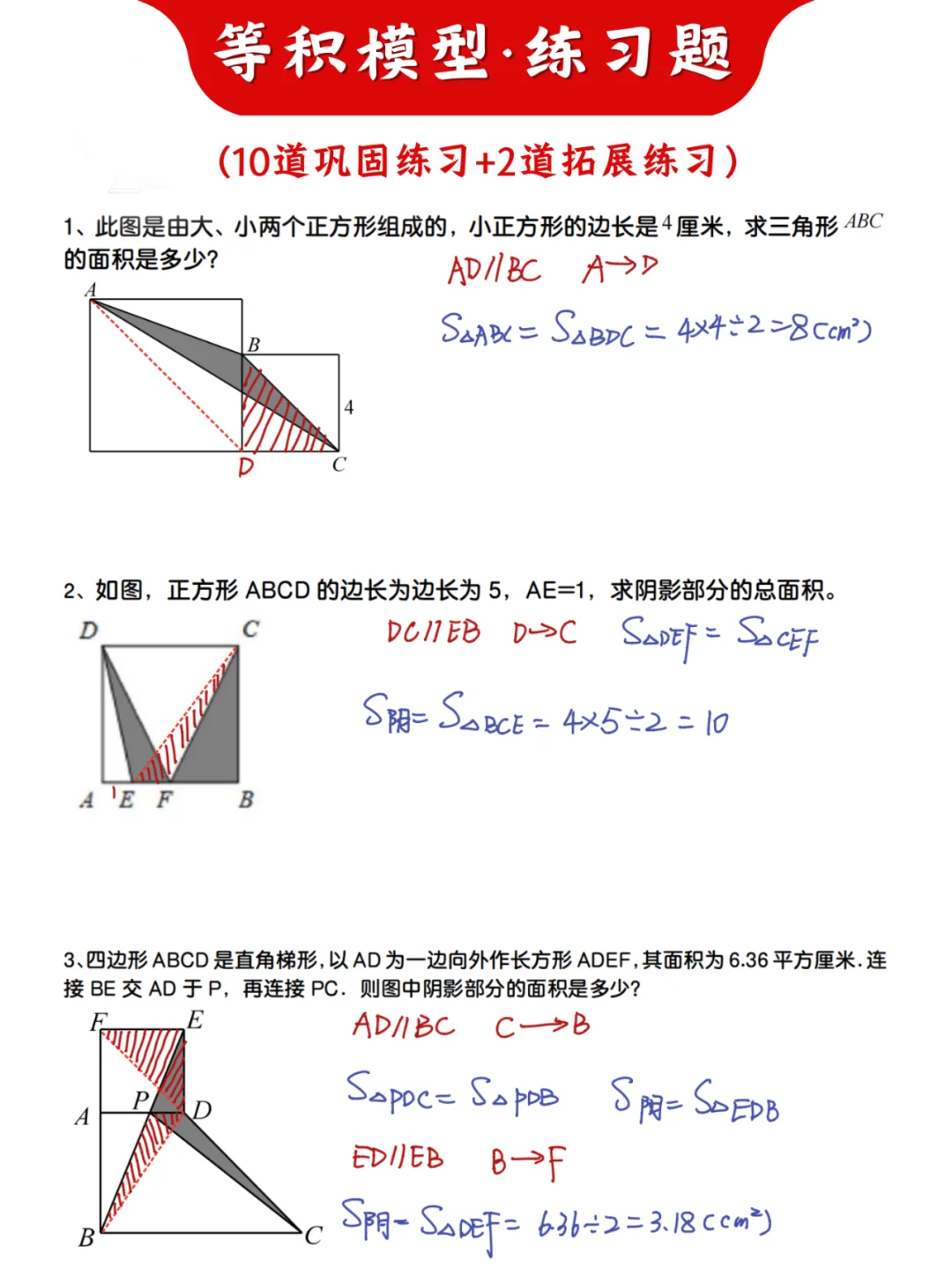
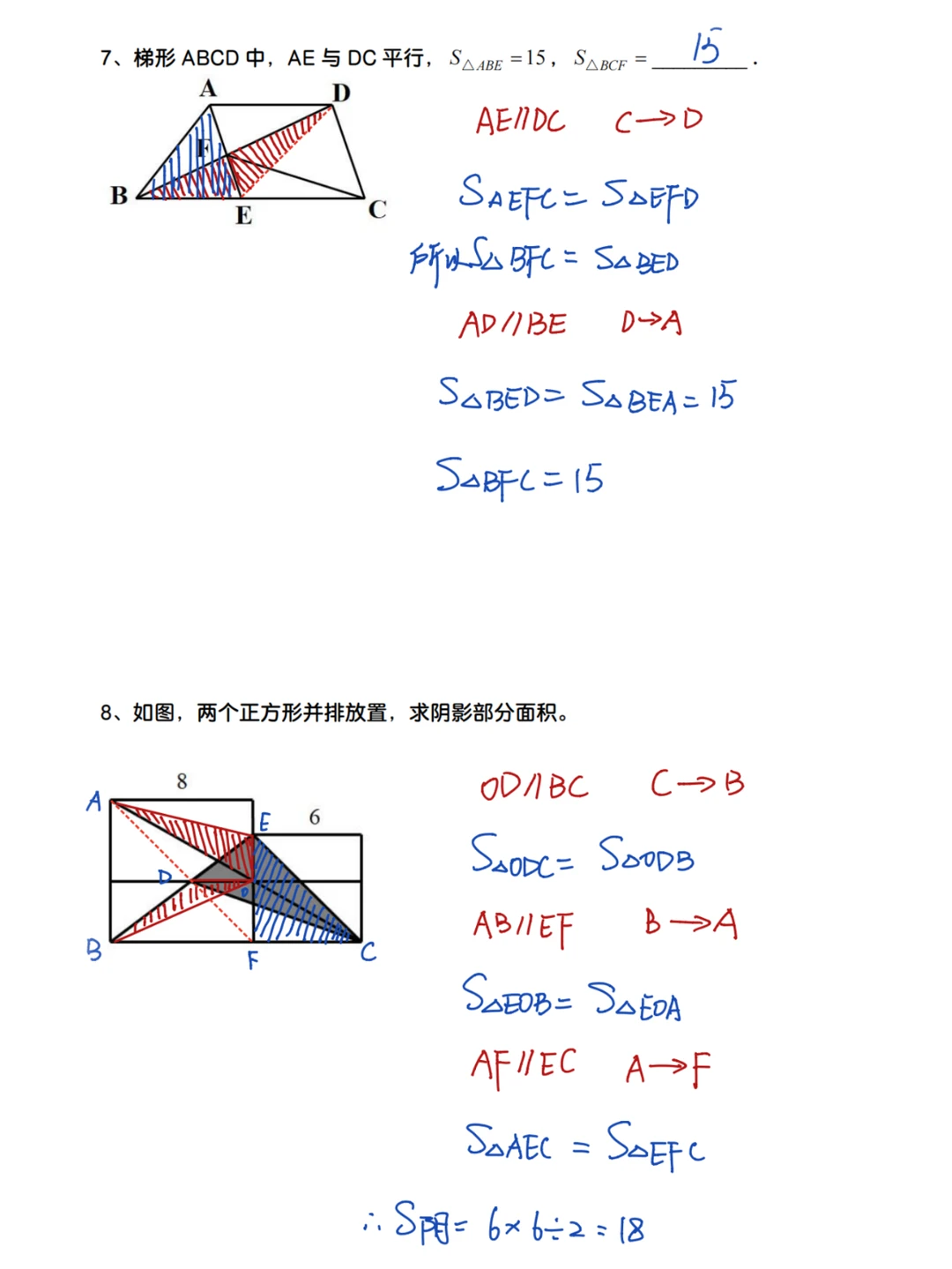
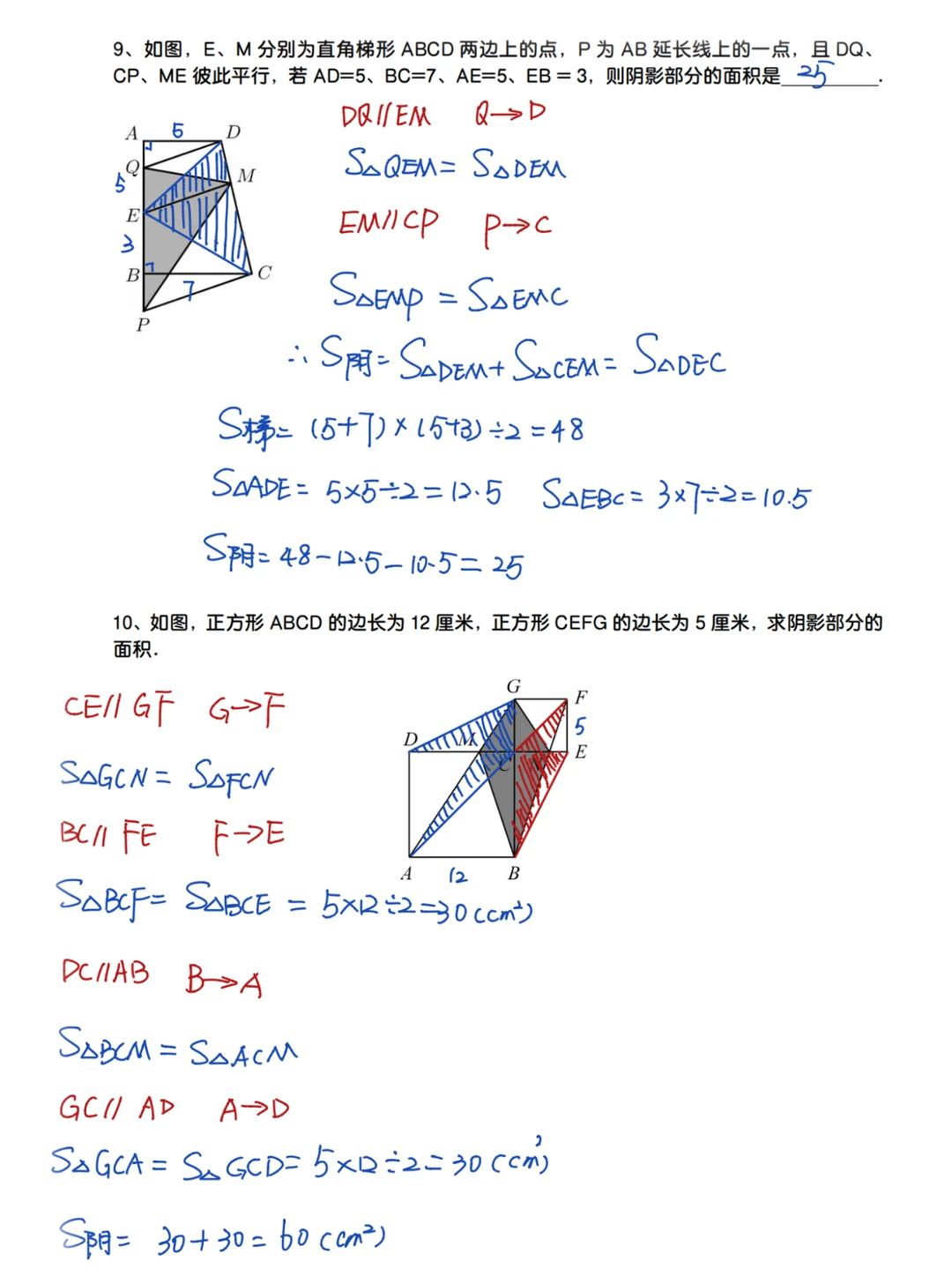
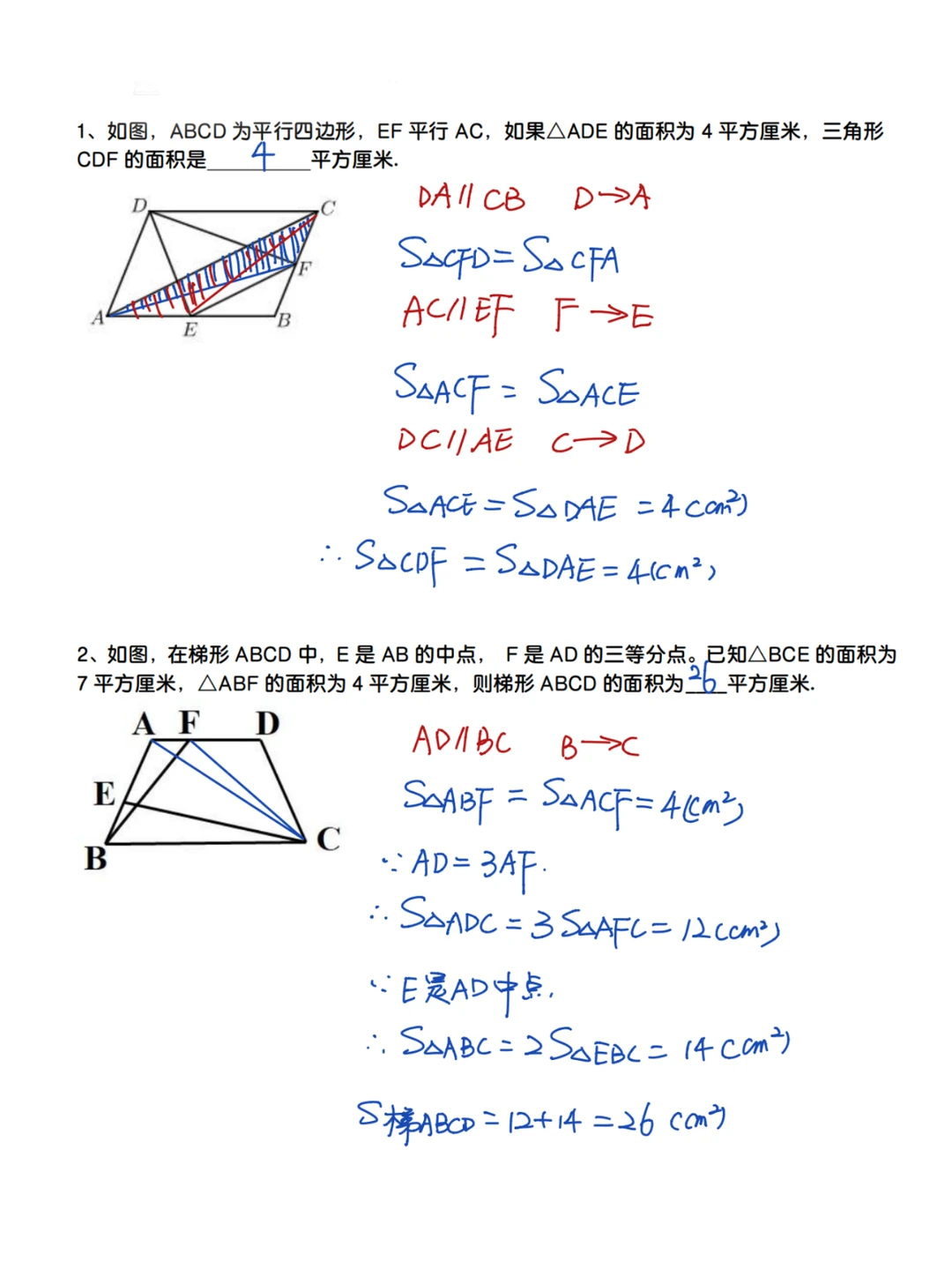
🌈等积模型的由来 已经知道三角形面积的计算公式： 面积=底*高/2 从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积． 如果三角形的底不变，高越大(小)，三角形面积也就越大(小)； 如果三角形的高不变，底越大(小)，三角形面积也就越大(小)； 这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的1/3，则三角形面积与原来的一样． 这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状。 ✅解题关键 1、面对形状或位置不太好的三角形面积计算，我们可以考虑将该三角形进行等积变形，如果要进行等积变形，核心点是要找到一组平行线； 2、正方形联排：几个正方形并排放置，不仅仅对边平行，还有同向的对角线平行，从而可以利用平行线间的等积变形解题。