[LG]《Stabilizing Native Low-Rank LLM Pretraining》P Janson, E Oyallon, E Belilovsky [Concordia University & Sorbonne University] (2026)

低秩分解（Low-Rank Factorization）一直被视为大模型训练和推理“减负”的希望，但如何在不依赖全参数模型引导的情况下，从零开始稳定地训练一个纯低秩模型？

本文提出了 Spectron 方案，不仅解决了低秩训练长期存在的崩溃难题，还揭示了低秩模型在计算效率上的惊人潜力。

以下是该研究的核心洞察与深度思考：

1. 核心痛点：为什么低秩训练总是“炸”？

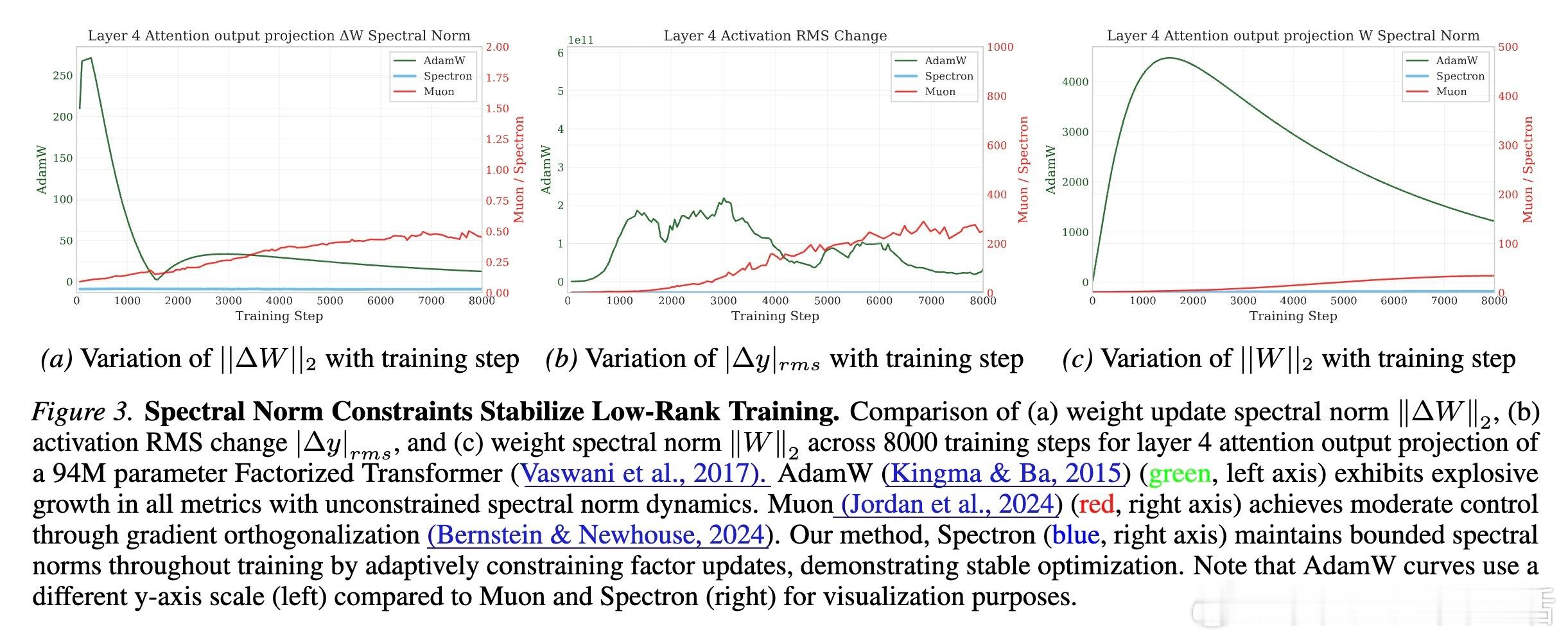
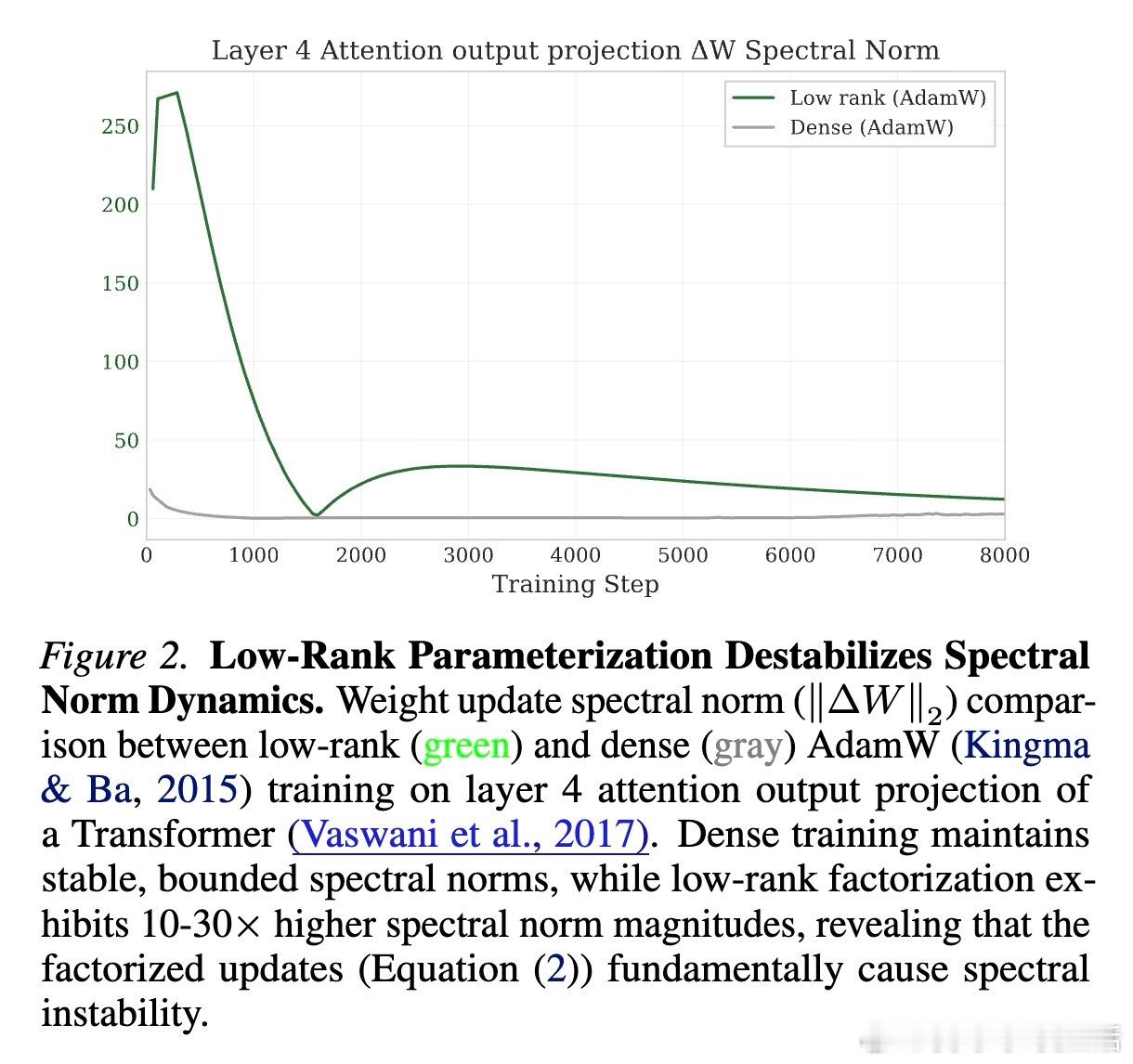
传统的低秩参数化（W = AB）在训练初期极度不稳定，经常出现损失函数激增（Loss Spikes）。研究团队发现，问题的根源在于“谱范数爆炸”。

在更新过程中，因子 A 和 B 的独立更新缺乏协同，导致乘积矩阵 W 的谱范数（最大奇异值）不受控地增长。这会引发激活值剧烈波动，最终导致训练崩溃。以往的方法通常需要保留一个全参数模型作为“导师”来引导，但这抵消了低秩带来的内存优势。

2. 破局之道：Spectron 的“谱约束”艺术

Spectron 引入了一种优雅的解决方案：带正交化的谱重归一化。

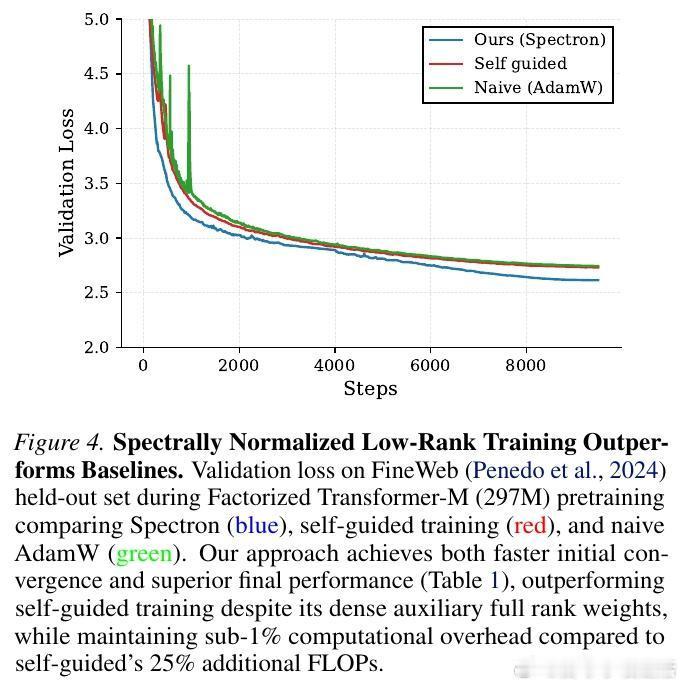
它通过动态调整因子 A 和 B 的更新幅度，将合成矩阵 W 的谱范数严格限制在一个稳定半径内。这种方法不需要任何全参数模型的辅助，仅需极小的计算开销（不到 1% 的 FLOPs），就能让纯低秩模型从随机初始化开始平滑训练。

3. 效率奇迹：同等算力下的“降维打击”

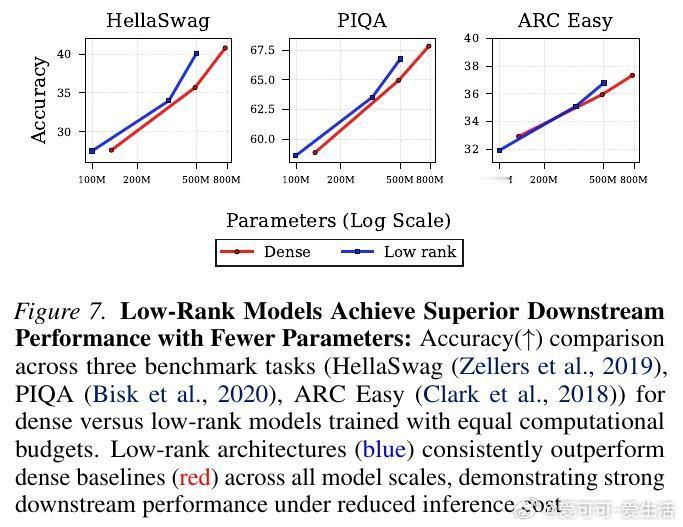
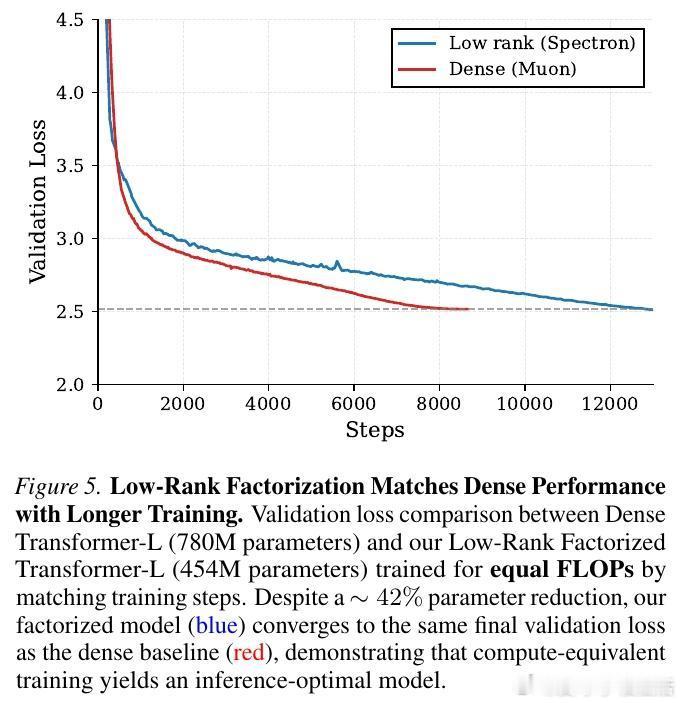
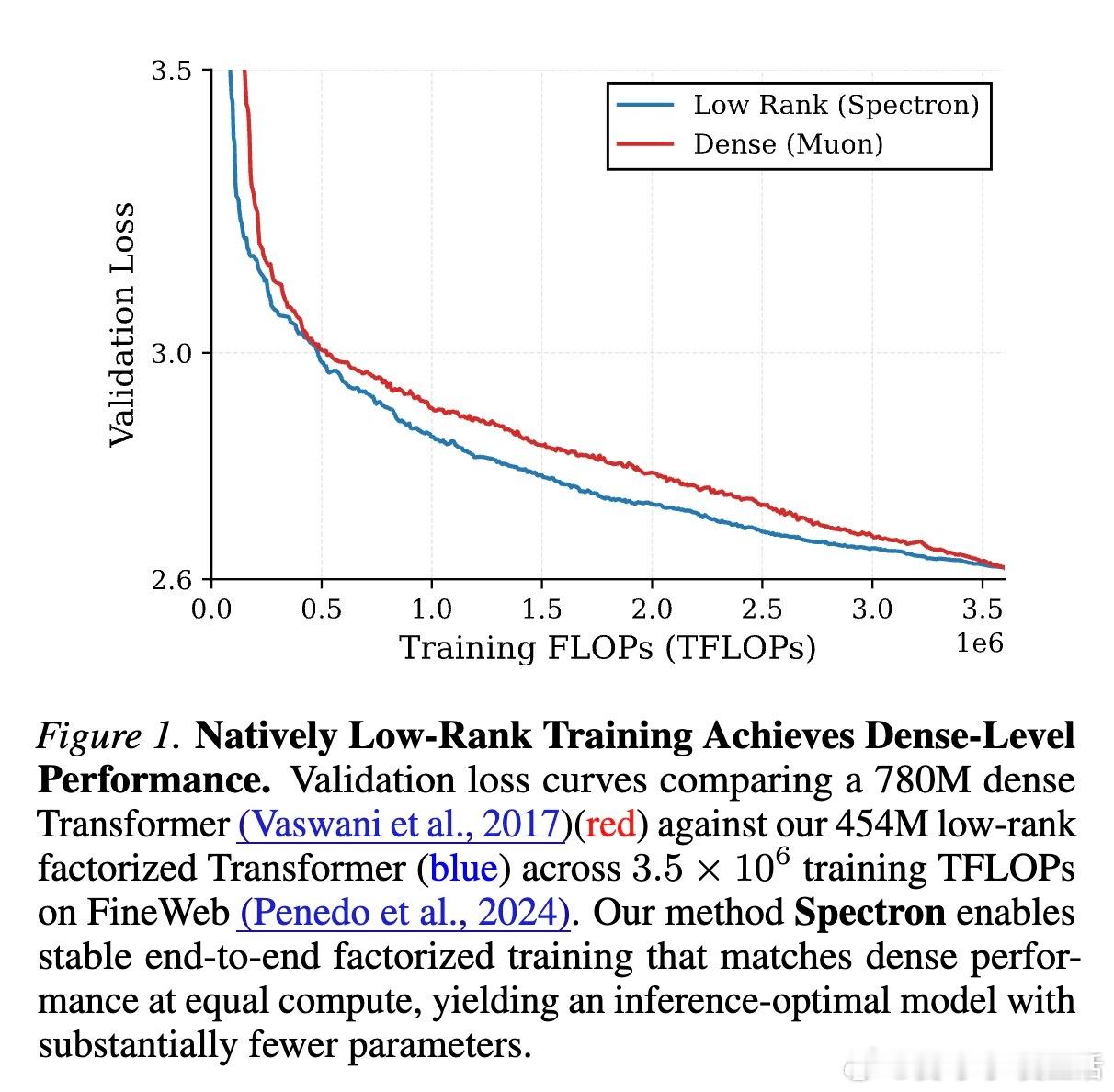
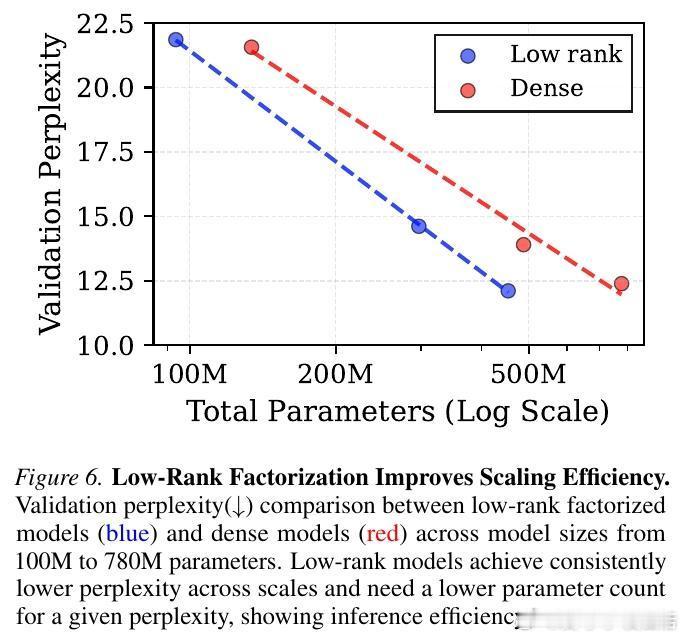
实验结果令人振奋：在相同的计算预算（FLOPs）下，Spectron 训练的低秩模型在验证集损失和下游任务表现上，完全匹配甚至超越了标准的全参数（Dense）模型。

这意味着，我们可以用更少的参数量实现相同的性能。例如，一个 4.5 亿参数的低秩模型，通过更长时间的训练，可以达到 7.8 亿参数稠密模型的水平。这为“推理优化”提供了全新的思路：在训练阶段多花一点时间，换取推理阶段巨大的参数量缩减。

4. 重新定义 Scaling Laws：低秩模型的生存法则

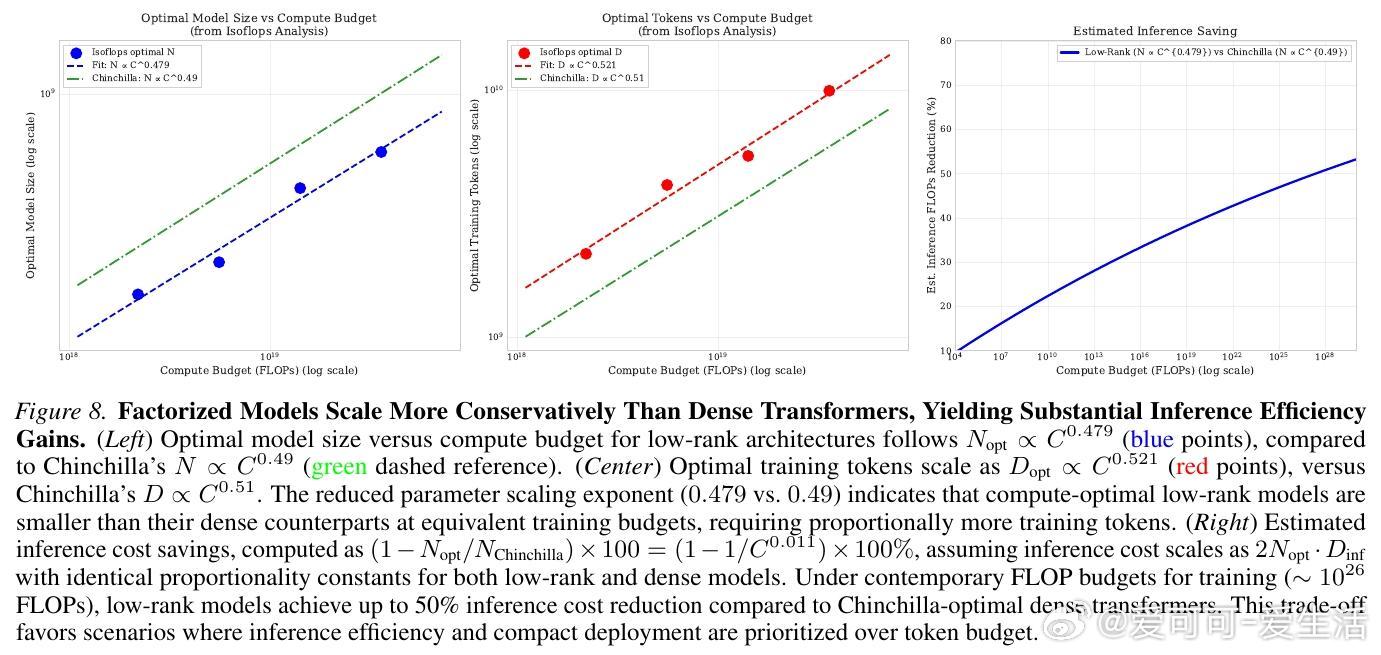
论文对低秩模型进行了系统的 IsoFLOP 分析，推导出了专属的缩放法则。

研究发现，低秩模型的计算最优（Compute-optimal）配置比稠密模型更倾向于“小模型、大数据”。在相同的算力预算下，低秩模型的最优参数规模更小，但需要喂入更多的 token。

这产生了一个极具启发性的结论：在数据充足的时代，低秩架构是通往极致推理效率的必经之路。

5. 深度思考：从“压缩”到“原生”的范式转移

过去我们习惯于先训练大模型再进行压缩（剪枝、量化、蒸馏），但这本质上是在修补一个低效的容器。Spectron 的成功暗示了一个更深刻的可能性：模型的能力或许本质上就是低秩的。

如果我们在初始化时就拥抱这种低秩特性，不仅能民主化大模型的训练（降低显存门槛），更能从底层逻辑上重塑 AI 的能效比。未来的大模型可能不再追求参数量的堆砌，而是在受限的秩空间内，通过更深度的训练挖掘智能的极限。

总结：- 智能的本质或许不在于参数的冗余，而在于结构的精炼。- Spectron 证明了：给更新套上“谱”的枷锁，才能换来训练的自由。- 低秩训练不是对性能的妥协，而是对推理效率的预支。

论文链接：arxiv.org/abs/2602.12429