今天的主题是介绍三角函数的积化和差公式，以及这些公式的用途。

山不在高，有仙则名，题不在多，精妙就行。本文只有一道例题，用多种方法解答。解法各有巧妙不同，都很精彩，希望得到读者的喜欢。

在三角函数式的恒等变形中，常常需要把三角函数积的形式转化为和差的形式。三角函数的积化和差公式共有四个，它们是今天的主角，请看下图：

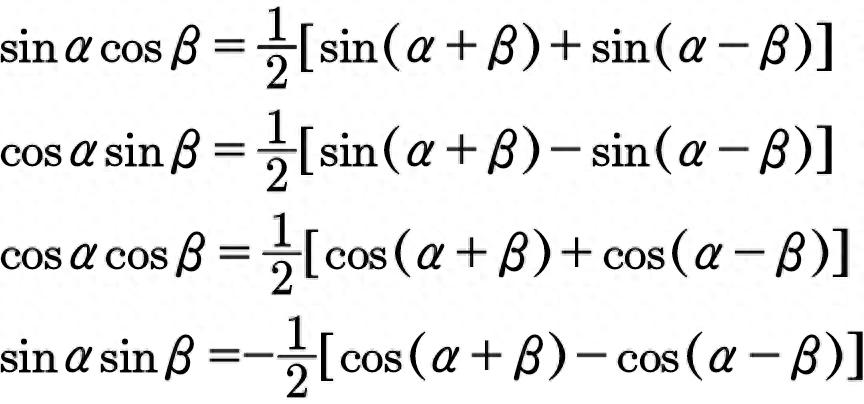
积化和差公式

这些公式不必死记硬背，我们可以用四大天王公式推导。

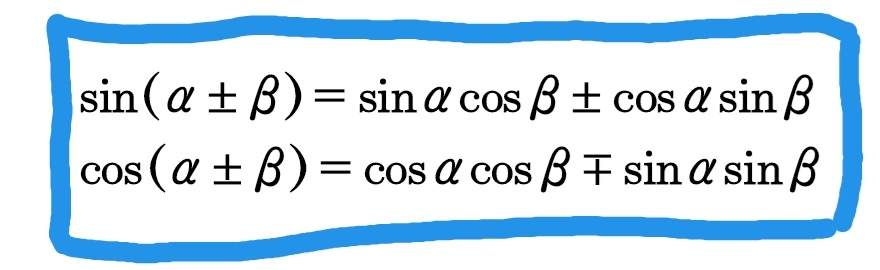
两角和差公式(四大天王)

三角函数的积化和差公式最主要的用途是把三角函数积的形式转化为和或差的形式，从而把乘法运算转化为加法或减法运算。这样，可以简化一些三角恒等变形问题。因此，这些公式常用于三角函数式的求值、化简和证明。此外，积化和差在微积分中是一种重要的变形方法。

应当注意，在化简和求值中，运用积化和差公式的目的，是使之产生特殊角或能相抵消的项或能相约的项。为此目的，在恒等变形中有时需要对三角函数式的分子分母乘以适当的项，然后利用积化和差公式，从而使变形朝着结果发展。

例题呈现

不查表，求

sin10°sin30°sin50°sin70°的值。

解题思路：由于不能查表计算，故应着眼于进行整体变形，化简。

解法一：

利用积化和差公式变形，将非特殊角化为特殊角达到求值的目的。

原式=½sin10°sin50°sin70°

=½sin10°·½(cos20°+½)

=⅛sin10°+¼sin10°cos20°

=⅛sin10°+⅛(sin30°-sin10°)

=⅛sin30°

=1/16

小结：

第一步是把sin30°特殊角的值½代入原式，

第二步用到了公式

sinα=cos(90°-α)

这个公式告诉我们余弦就是余角的正弦。于是变形为

½sin10°cos40°cos20°

再根据cosαcosβ的积化和差公式得到

½sin10°cos40°cos20°

=½sin10°·½(cos20°+cos60°)

=½sin10°·½(cos20°+½)

第三步需要去括号，我们把

¼sin10°作为一个整体去乘以括号里的项，就得到第三步。

第四步是使用cosαsinβ的积化和差公式的结果。

第五步，使用积化和差公式后产生了能够抵消的项，于是化简为⅛sin30°。

这时，我们惊奇地发现，所有的非特殊角都不见了，只剩下一个特殊角。于是轻松得到答案：1/16。

解法二

这个解法要用到二倍角公式：

sin2α=2sinαcosα

把正弦函数化成余弦函数后，反用倍角公式求值。

原式

=cos20°cos40°cos60°cos80°

=½cos20°cos40°cos80°

=sin40°cos40°cos80°÷4sin20°

=sin80°cos80°÷8sin20°

=sin160°÷16sin20°

=sin20°÷16sin20°

=1/16

小结：

请把上面的➗号看作分数线，把➗号左边看作分子，右边看作分母。(下同)

第一步用到了公式

cosα=sin(90°-α)

第二步把cos60°=½代入，

第三步把第二步改写成分式，分母为2，再用2sin20°去乘以分子分母，利用倍角公式，把

2sin20°cos20转化为sin40°

第四步，分子分母同时乘以2，把2sin40°cos40°转化为sin80°

第五步，故技重施，还是同样的套路，

第六步用到了公式

sinα=sin(180°-α)

产生了可以约去的项，于是顺理成章得到答案：1/16。

本题的几何意义

请看下图：

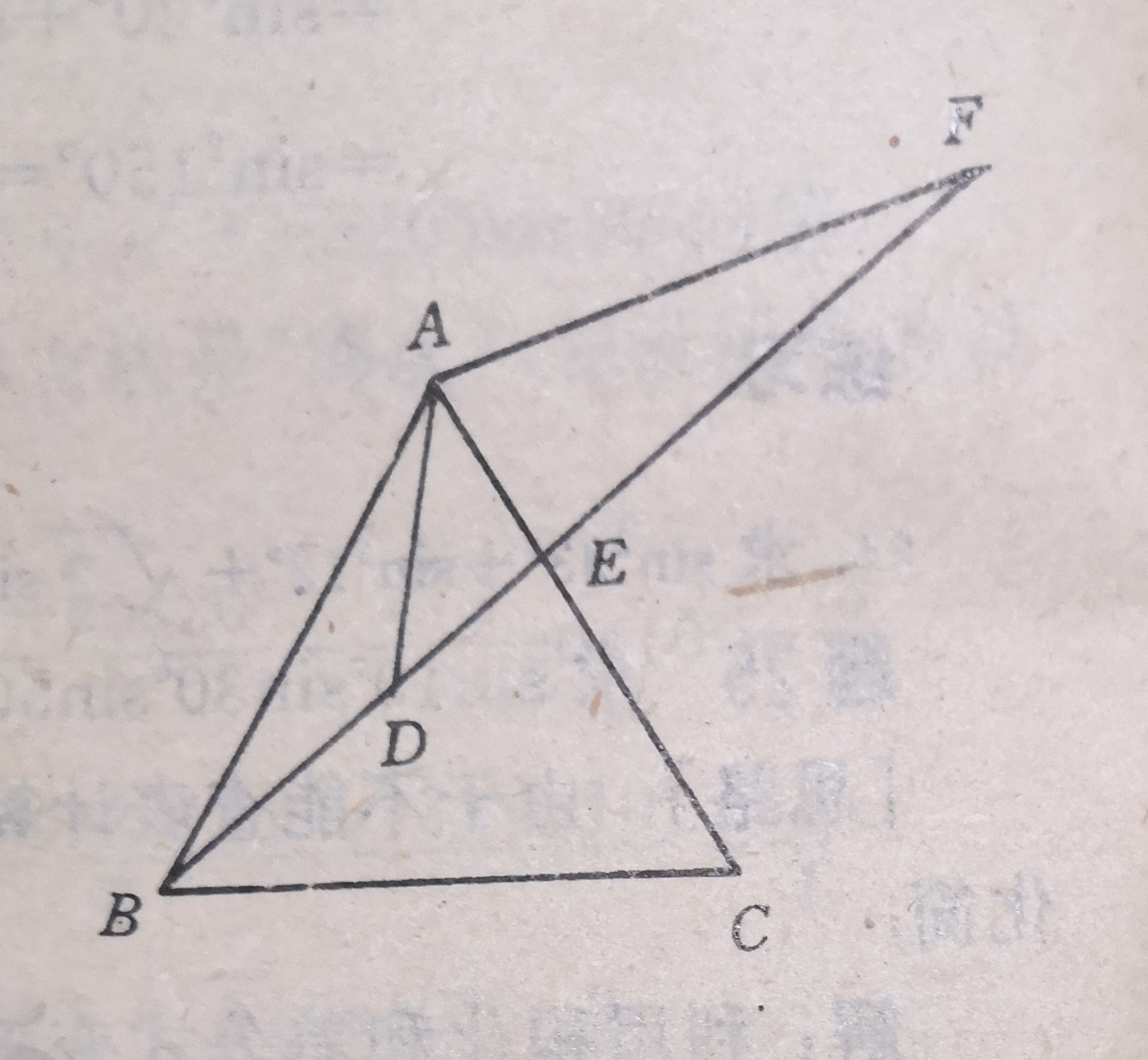
上图所示的作图法是：作等边三角形ABC，过B作BF，使∠ABF=20°，AF=AB，过A作AD，使∠BAD=20°，AD交BF于D。

△ABD是等腰三角形，∠ADB=140°，所以

∠ADE=40°，△ADE是等腰三角形，且∠AED=100°，所以

∠AEF=80°，△AEF是等腰三角形。

上图构思巧妙，大等腰三角形ABF由三个小等腰三角形组成。

于是，根据等腰三角形三线合一的几何性质，得到

cos20°=½AB÷AD=AB÷2AD

cos40°=AD÷2AE

cos80°=AE÷2AF=AE÷2AB

以上三式相乘，相同的项成对相消，得到

cos20°cos40°cos80°=⅛

于是原式的值=½×⅛=1/16。

你学会了吗？

给大家留一道题作为家庭作业：

不查表，求

sin20°sin40°sin60°sin80°的值。

总结：本文虽然只有一道例题，但是在解题过程中，展示了高超的解题技巧，非常漂亮。

今天是中秋节，祝大家节日快乐。团圆是中秋节的主题，祝大家阖家团圆，幸福美满；奋斗是我们共同的底色，祝大家日子过得红红火火，越来越好。

科学尚未普及，媒体还需努力。感谢阅读，再见。