八大金刚公式记忆方法

今天我们的主题是探讨同角三角函数有哪些基本关系式？如何理解、推导和记忆？

上期文章我们谈到了四大天王公式，今天就该讨论八大金刚公式了。

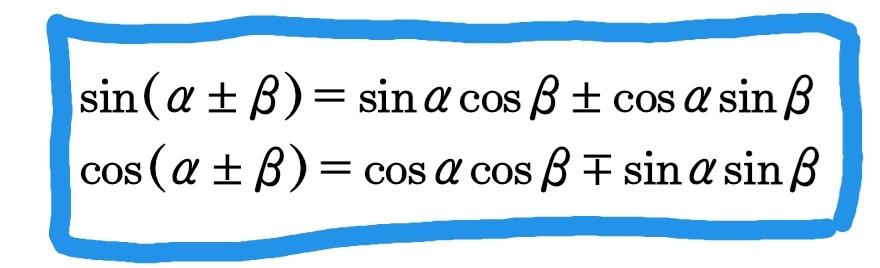
四大天王公式

根据三角函数的定义，可以得到同角三角函数间的以下八个基本关系式(八大金刚公式)：

倒数关系三个

倒数关系(公式1～3)

商数关系两个

平方关系三个

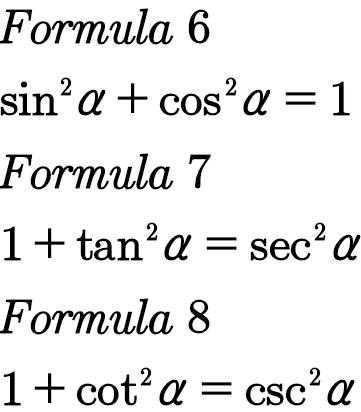
实际上，同角三角函数间的关系式共有36个(以上三类共八个公式是最常用的)，其中关于和、差、积、商的关系式分别有3、6、9、18个(和3，差6，积9，商18)。

这36个公式不难从以上八个基本关系式(八大金刚公式)变形得到，读者不妨试试。虽然这许多公式用不着死记硬背，但熟悉它们对于三角恒等变形是有益的。

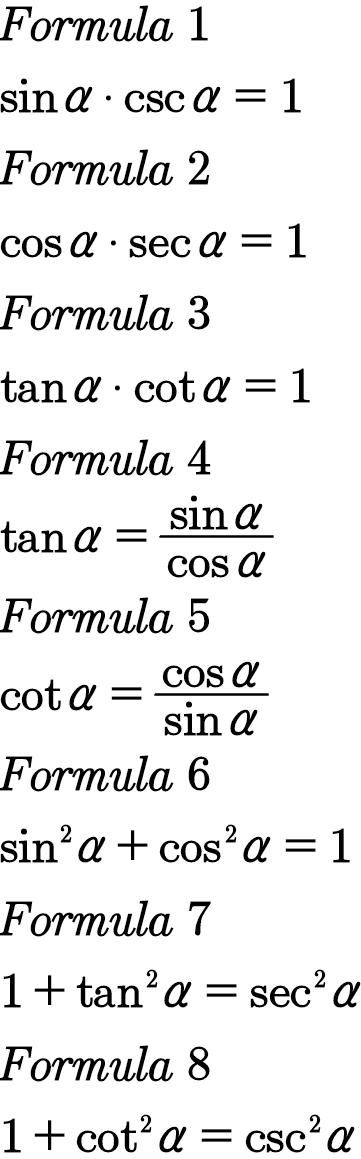
八大金刚合影

公式6怎么证明？方法很多，推荐阅读下面的文章：(我的往期文章)

【如何用三角函数证明勾股定理？ - 今日头条】

点击链接打开 https://m.toutiao.com/is/fRLCvl0_fEQ/ fRLCvl0_fEQ` pib:/ e@o.Dh :4am

复制此条消息，打开「今日头条APP」或「今日头条极速版APP」后直接查看~

【兰道：优秀的严谨主义者 - 今日头条】

点击链接打开 https://m.toutiao.com/is/Xp_4B2KIp64/ Xp_4B2KIp64` dvX:/ e@o.Dh :8am

复制此条消息，打开「今日头条APP」或「今日头条极速版APP」后直接查看~

证明方法一言以蔽之，就是把勾股定理公式a²+b²=c²两边同时除以c²，就得到公式6。

我们在学习八大金刚公式时，应该注意以下问题：

(1)在以上八个公式中，只有类似勾股定理的公式6是绝对恒等式，其余7个公式只当α取使公式两边都有意义的值时才能成立。以后我们遇到的三角函数式，三角恒等式也都是这样。

例如，当α=90°时 tanα和secα不存在，所以对于α=90°的情形，公式2、3、4、7都不成立。但是对于使等式的两边都具有意义的那些角来说，不论角的终边在哪个象限，等式都成立。因此，它们都是恒等式。

(2)在将公式进行变形(以后三角函数式的变形也是这样)过程中，三角函数的定义域有时会发生变化。例如公式4及其变形：

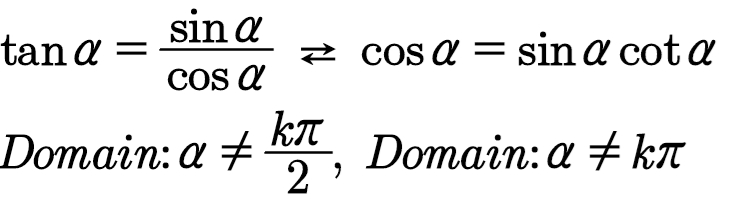
注意定义域的变化

前者的定义域是α ≠½kπ，后者的定义域是α≠kπ。注意这一点对于学习三角方程的增根、失根情况的讨论是十分必要的。

(3)八大金刚公式反映了它们之间的内在联系和规律。由于这八个公式只涉及到了六个三角函数，因此在它们中间仅有五个(公式1、2、3、4、6)是独立的或最基本的，其余三个(公式5、7、8)可以从这5个公式推导出来。

例如，公式5可由公式3和4推出：

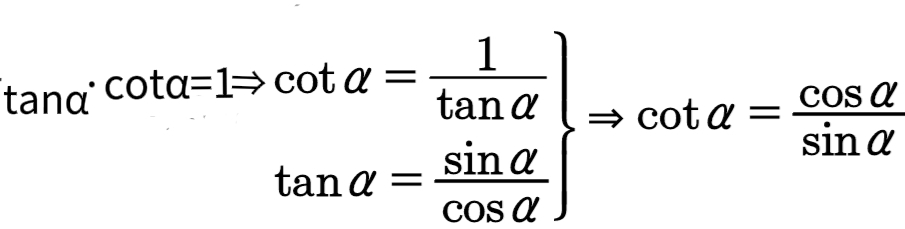
(4)要注意这些公式的结构和特征，特别要重视成立的条件，明确“同角”的意义。例如

sin²(α-β)+cos²(α-β)=1

但是

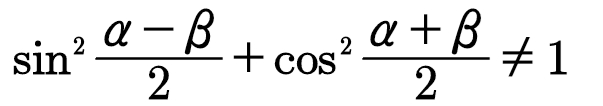
等等。

同角三角函数间的基本关系式(八大金刚公式)是三角恒等变形的重要公式之一，应该熟练掌握和运用。通常记忆这组公式的方法有两种：

第一种记忆方法：

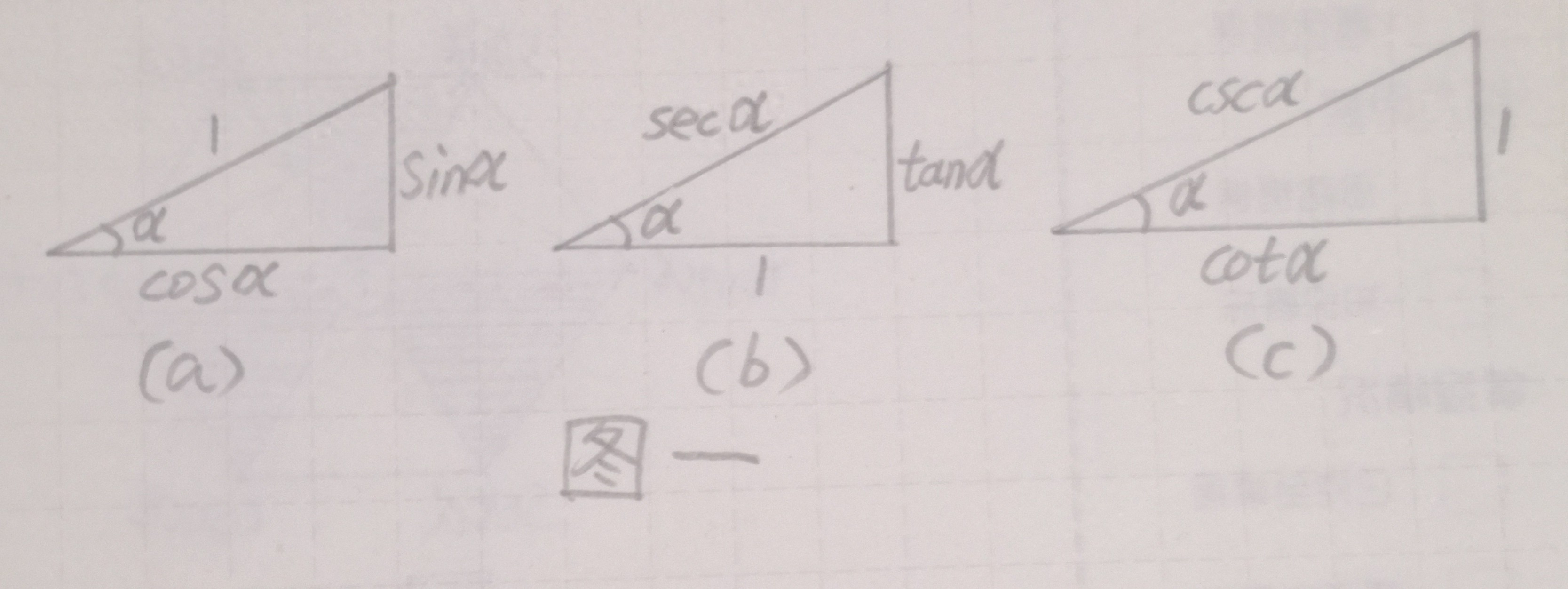
图一

作一个直角三角形，设其中一个锐角为α。如果α的对边为a，邻边为b，斜边为c，则有

在图一(a)中，三边同除以c，则斜边为1，对边=a/c=sinα，邻边=b/c=cosα。

根据三角函数的定义，得

tanα=sinα/cosα，

cotα=cosα/sinα，

secα=1/cosα，

cscα=1/sinα；

根据勾股定理，还有

sin²α+cos²α=1；

在图一(b)中，三边同除以b，则有邻边为1，对边为tanα，斜边为secα，在图一(c)中，三边同除以a，则对边=1，邻边=cotα，斜边=cscα，

因此，

cotα=1/tanα，

sec²α=1+tan²α，

csc²α=1+cot²α.

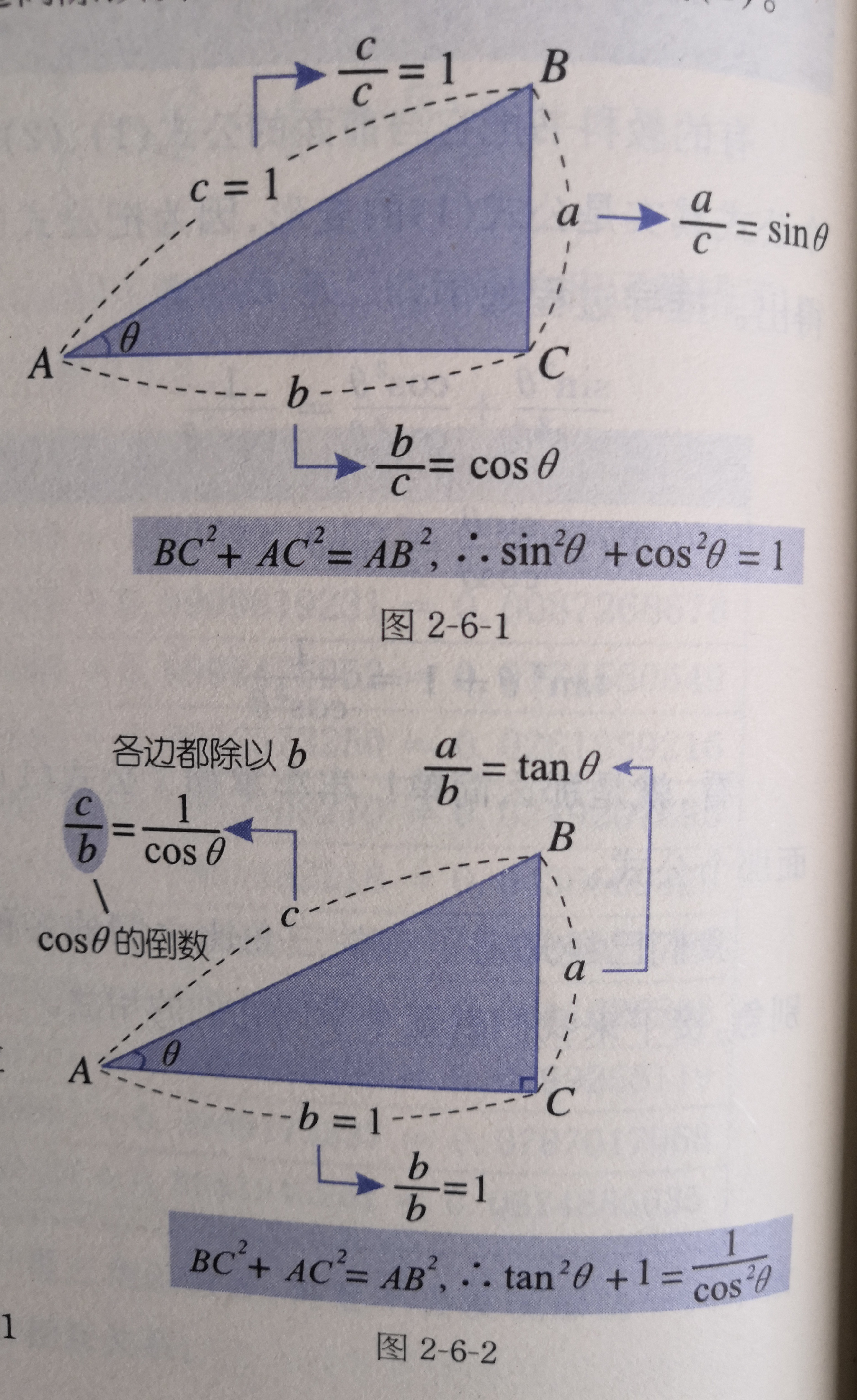
这就得到了同角三角函数间的八个公式。

第二种记忆方法：如图二，方法是：

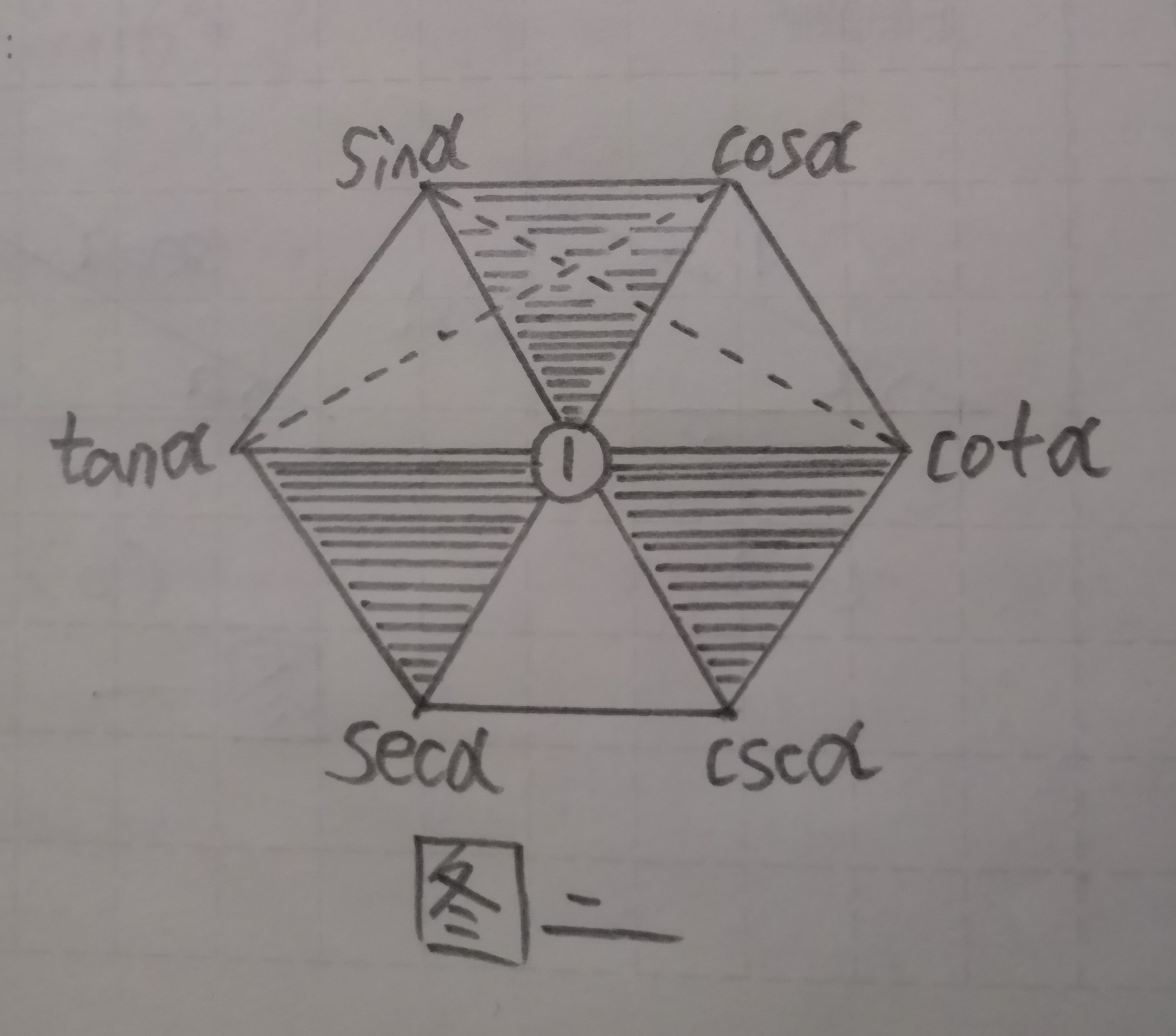
①在对角线上的两个三角函数值的乘积等于1。

例如 tanα·cotα=1；

②在带阴影的三角形中，上面两个顶点上的三角函数的平方和等于下面顶点上的三角函数的平方。

例如，1+tan²α=sec²α；

③任意一顶点上的三角函数等于相邻两个顶点的三角函数的乘积(主要是二虚线两端的三角函数的乘积)。

例如sinα=cosα·tanα，

cosα=sinα·cotα，

这两个公式变形后即可得到商数关系的两个公式。

公式7和8可以变形如下图所示：

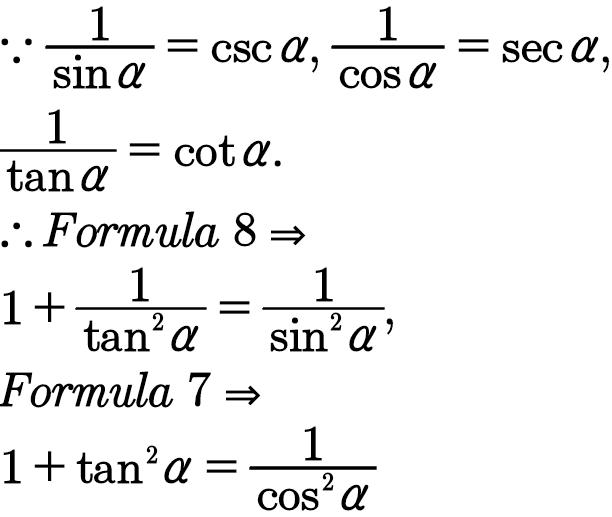
计算器上只有sin，cos，tan这三个按键，六个三角函数的其余三个没有按键怎么办？

计算器是死的，但人是活的。通过恒等变形，三个按键也够用了。

运用之妙，存乎一心。

——［南宋］岳飞

《兰道：优秀的严谨主义者》截图

科学尚未普及，媒体还需努力。感谢阅读，再见。