开场故事

这里我想引用印度数学天才拉马努金的故事说明数论学者与自然数的“情谊”。

这位来自印度最南端泰米尔纳德邦的办事员具有快速且深刻地看出数的复杂关系的惊人才华。

著名的英国数论学家G·H·哈代在1913年“发现”了他，并于次年邀他来剑桥大学。哈代在有一次去探望病中的拉马努金时告诉后者，自己刚才乘坐的出租汽车车号是1729，是一个很无趣的数字。

拉马努金立即回答：“这是一个很有意思的数，1729是可以用两种方式表示成两个自然数的立方和的最小的数。”（既等于1的三次方加上12的三次方，又等于9的三次方加上10的三次方。）哈代又问，那么对于四次方来说，这个最小数是多少呢？拉马努金想了想，回答说：“这个数很大，答案是635318657。”（既等于59的四次方加上158的四次方，又等于133的四次方加上134的四次方。）讲述人：蔡天新

外一则——华罗庚的车牌

讲述人：贼叉讲了这么多关于整除的知识点，我不禁又想起了华罗庚先生。华先生真的是难得一见的天才，一个没有接受过系统高等教育的人，仅凭自学就达到这样的高度，实在难以想象华先生的天赋得有多高啊。而且，华先生不光做数学研究，还非常热衷于推广数学，这是非常难得的。苏联人在这方面曾做得很好。在我国，华老就是领头羊。他撰写了一系列的科普文章，还经常给中学生做报告，现在想来，这些孩子是多么幸福啊。 华先生对于数学思想的领会极其深刻，而且对于不同阶段的学习者有什么要求，他也了如指掌。对于初学者，他就强调数形结合。所谓“数少形时难直观，形少数时难入微”，就是出自他口。同样，他也非常强调计算能力的培养。 在长期的数学学习和教学中，我也是逐步体会到华先生的伟大之处的。 所以我也一直强调:计算是基本功。无论你以后是否从事数学研究，计算过关都是重要的。 你知道华罗庚先生的心算有多强吗？

他可以心算六阶行列式。有没有跪了？ 什么？行列式是啥？

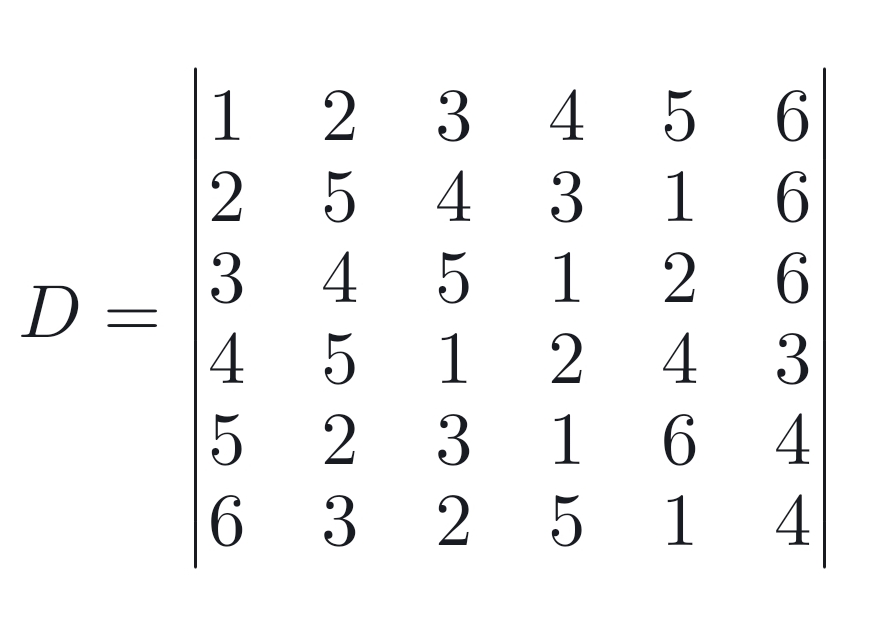
化简后求出这个行列式的值为-972

这个计算就是理论上每项有6个数相乘，共720项加加减减，当然实际上项数会少很多，但是华老做的心算，就算化简下来，怕也是有几十项或一百多项。 还有一次，华老带着自己的研究生和一些中学老师散步，途中看见一辆车，然后就问:“这个车牌能被7整除，但不能被11和13整除，为什么？” 大家一看，这个车牌号是31-03219,去掉连接号就是3 103219。大家都惊呆了:这算得也太快了吧！ 这里我们回忆一下能被7，11,13整除的数的特点:用最后三位数字组成的数减去前面剩下的数字组成的数，如果所得的差是能被7，11,13整除的数，那么原数也就能被这三个数整除。但是，华老怎么能算得这么快呢？ 啊，刚才华老好像抬头看了一眼云，难道这就是所谓的云计算？ 华先生一看大家没反应，就笑嘻嘻地说:“晚上到我房间坐坐。”然后扭头跟研究生们说:“如果你们想出来了，就和中学老师们一起来；如果想不出，就别来了......” 你们体会一下当时研究生们的心情.....

当天晚上，“好奇宝宝”中学老师组团如约而至，华先生又问一遍，还是无人作答。于是，华老公布答案了。7,11,13这三个数有个很棒的最小公倍数——1001,要验证一个数能不能被这三个数整除，可以借助看这个数是不是1001的倍数来判别。3 103219这个数，从头往下砍，可以看出3003000是1001的倍数，去掉3003000后还剩下100219，再去掉100100，剩下119，而119=7×17,所以，3103219这个数只是7的倍数，而不是11和13的倍数。 中学数学老师们再次集体惊呆。 什么叫“举一反三”？什么叫“活学活用”？这就是例子。日常的积累非常重要，对于那些特殊的数，要经常拆一拆、组合组合，烂熟于心，对提升计算速度和准确率都是有好处的。 顺便说一句，据说，华先生带的那群研究生，那晚一个人都没敢去。