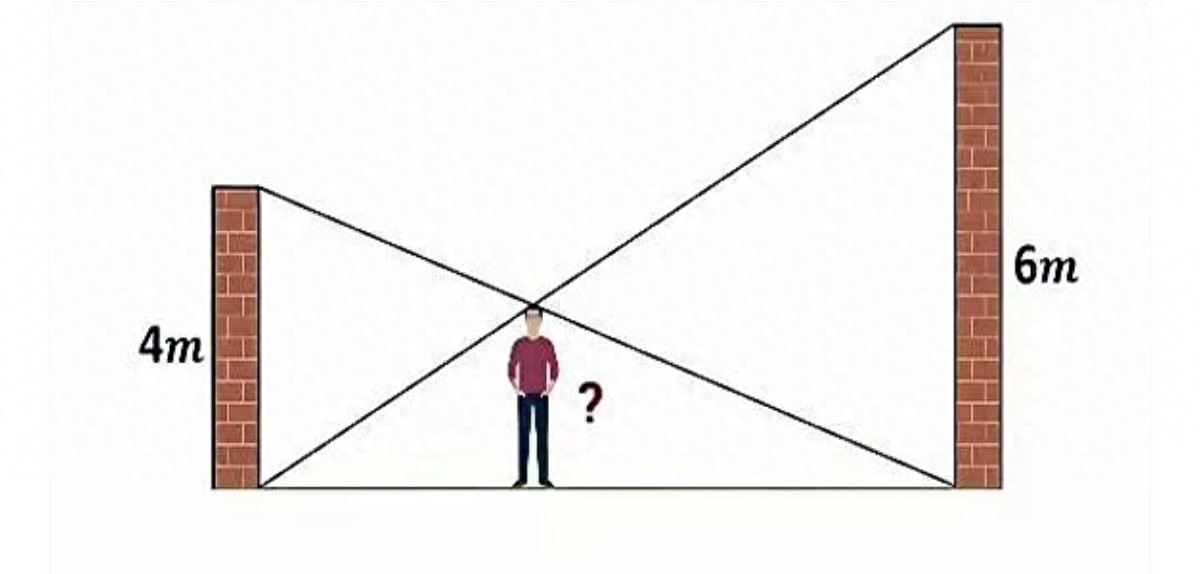
基本图

如图所示，已知两堵墙的高度分别是4米和6米，求上图男人的身高。

很多人看到题目就傻眼了，两堵墙的距离是未知数，条件不足，男人的身高没法求啊？

其实不是条件不足，而是刚刚好。如果告诉你两堵墙的距离，则条件冗余。

题目有不合理的地方，最后算出来的身高超过姚明了。让我们忽略这个bug，看看应该如何解题。请看解答图：

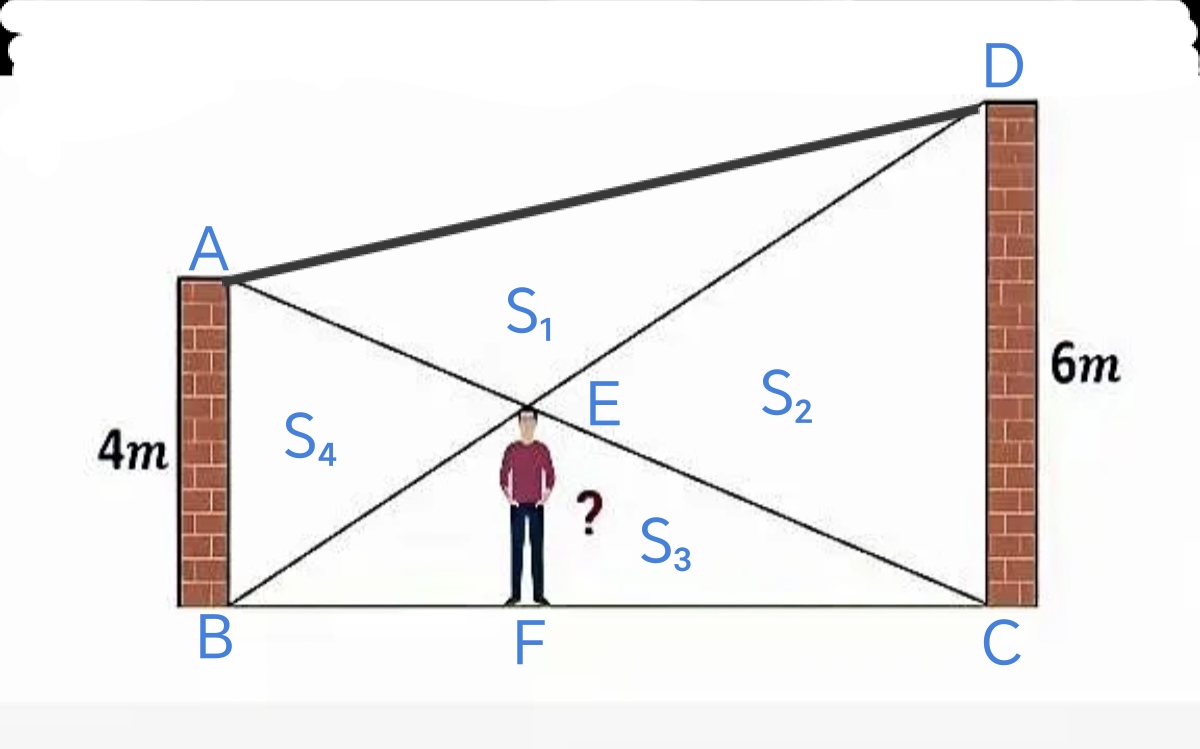
解答图

审题：ABCD是直角梯形，上底AB=4米，下底CD=6米。梯形的两条对角线相交于点E，EF⊥BC，垂足是F。求EF的线段长度。

梯形的两条对角线把梯形分为四个三角形，根据蝴蝶模型的结论，有

S₁=S₃，且S₁·S₃=S₂·S₄和S₄:S₂=2²:3²

字母S表示三角形面积。

两堵墙的距离BC是变量，EF却是常量。对于这一点，很多人觉得奇怪。

其实很容易理解。不管BC如何变化，我说梯形的中位线永远等于5米，没有人反对吧。

这是显而易见的。梯形的中位线平行于上下底，长度为上下底之和的一半。

如果延长EF交AD于点G，根据蝴蝶模型的结论，则有GE=EF。

从梯形的中位线是常量这个结论，可以推广到更普遍的一般情况。GF和中位线平行，它的一半等于男人的身高，我们可以给它取个名字，称为定比中位线。

请看解答图，因为三角形ABE和三角形CDE相似，且相似比为2:3，故点F是线段BC的定比分点，有BF:CF=2:3。所以，我们把GF称为定比中位线。

出题老师告诉我们，梯形不仅中位线是常量，而且定比中位线也是常量。

我们来验证一下。不妨设BC=10，设EF=a，因为三角形ABC和三角形EFC相似，故

4:10=a:6，所以a=2.4

再设BC=5，则有

4:5=a:3，所以a=2.4

得到一个结论：因为BF:CF=2:3，所以定比中位线GF=2EF=4.8

中位线是特殊的定比中位线，把梯形的两腰分为1:1。不管定比是1:1还是2:3，只要定比确定，那么定比中位线的长度就是常量。

举个例子。设梯形的定比中位线JK分BC为两段，K在BC上，且BK:CK=1:2,求JK的长度。

解：设JK=a，设变量BC=h，则梯形ABCD的面积为5h。

看到这里，读者已经知道我们要用仁者无敌面积法求解JK的线段长。

面积法就是利用面积关系解题，列出面积方程，求解未知量。

解题过程请看下图：

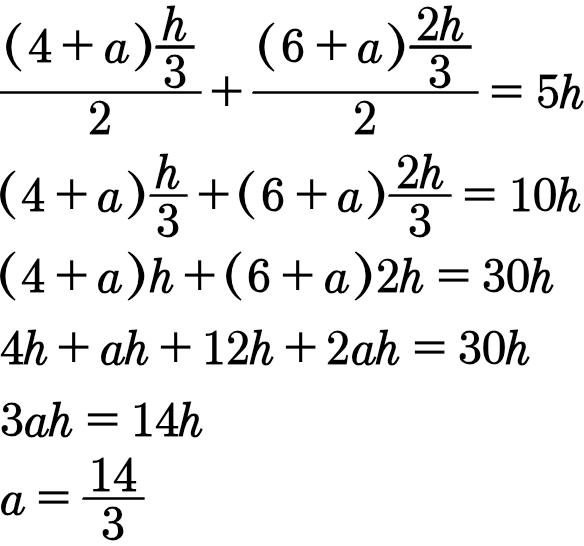
定比中位线JK平行于AB，把直角梯形ABCD分为两个直角梯形，即ABJK和JKCD。这两个梯形面积之和为5h平方米。

因为JK是常量，所以最后得到答案：

JK=a=3分之14.

科学尚未普及，媒体还需努力。感谢阅读，再见。

今天是情人节，祝天下有情人终成眷属。情人节快乐[玫瑰][礼物][红包]