题目呈现：把圆周展开为一条线段。

对于许多实用上的目的来说，用阿基米德算出来的约率(3又7分之1)来代表π的数值已经足够了。把一个圆的3又7分之1个直径量到一条直线上的话，就等于把这个圆周展开了(我们知道把一条线段分为7等分不是一件难事)。木工，白铁工们另外有一套展开圆周的简便方法，这里我们不打算一一介绍了，只预备介绍一个相当简单而且相当精确的展开方法。

假如我们想把一个半径r的圆O的圆周展开(图123)，那么，作出直径AB，在B点作和AB垂直的直线CD。从圆心O作一直线OC和AB成30°角，然后令CD等于半径的3倍长度，即CD=3r，连接AD，AD的长度就等于半个圆周的长度。把AD延长一倍，就得到圆周展开后的长度近似值。这种方法可能发生的误差相当小。

问：这个方法有什么根据呢？

在三角形OCB中，由勾股定理可得

CB²+OB²=OC²

用r表示半径OB。此外，CB=½OC(因为∠COB=30°)

所以，上式可以改写成

CB²+r²=4CB²，所以r²=3CB²

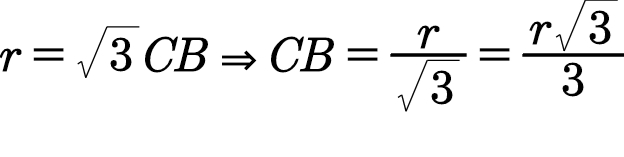
然后，在三角形ABD中，

根据勾股定理可得

把上面的结果与用π取3.141593所算出来的结果相比的话，可以看到两者之间只差0.00006r。假如我们用这个方法展开半径为1米的圆周，那么对于半个圆周所产生的误差一共只是0.00006米，对于全圆周来说误差也不过是0.00012米或0.12毫米罢了(差不多是头发的粗细)。

以上内容引自《趣味几何学》，作者是苏联科普作家别莱利曼，译者是符其珣，中国青年出版社2008年3月，第三版。

科学尚未普及，媒体还需努力。感谢阅读，再见。