
这让我思考了一会儿。
过了一会儿,我插入了 0 到 10 之间的随机数,只是为了看看是否有任何数字可以完美地适合表达式。
猜猜怎么了?我得到了两个数字
您可以暂停片刻,然后尝试这种方法来查看适合的数字。
你得到了什么数字?
现在,我们做一些数学推导来看看这些值是如何得到的。
提示:对两边取自然对数。
拿起笔和纸,尝试一下。我很想在评论中看到你的方法。如果你做对了,就击掌!但如果做错了,也不要着急——跟着做就行了。
如果这个挑战引起了你的兴趣,请查看下面的其他谜题列表!
你准备好了吗?让我们开始吧!
这个问题看起来有点吓人,但我们可以对两边取自然对数来让自己舒服一点。

这给了我们以下信息:

请注意,等式左侧有Inx 。我们可能还希望右侧有Inx ,以便我们可以轻松地对该项进行分组。
为此,我们将表达式重写如下:

这给了我们:

太棒了!从这里,我们得到了这个:

现在,我们两边都有Inx 。太棒了!
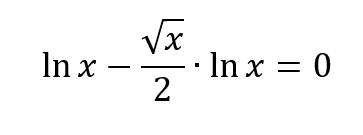
现在我们可以分解因式了!

这是两个项的乘积。结果为 0。这意味着Inx或(1-sqrt(x)/2)为零!
如果我们认为x为零,
Inx = 0
我们可以对两边取幂。这样我们得到:

请记住,具有给定参数的自然对数函数的指数将得出该参数,并且任何数字的零次方都是 1。这给了我们:

另一方面,如果我们考虑1-sqrt(x)/2 = 0,那么我们将得到:

你答对了1和4吗?太棒了!