加法魔方大家都见过，就是幻方。网上看到的美国数学竞赛题很有意思，是乘法魔方。

题目呈现

每个字母表示一个不为零的自然数，三横三纵两条对角线的乘积等于一个常数，求左下角的数。

常见的幻方是这个样子的。

4，9，2

3，5，7

8，1，6

幻和等于15.

加法和乘法的最大不同是什么？我以为是混合物与化合物的区别。

举个例子。

30=3×5×2

30=15+8+7

我用这道题考小明同学(化名)。

小明同学很厉害，年轻人反应快，头脑里一阵思维风暴，很快给出了答案。

上图是他的演算草稿。

他给出的答案是

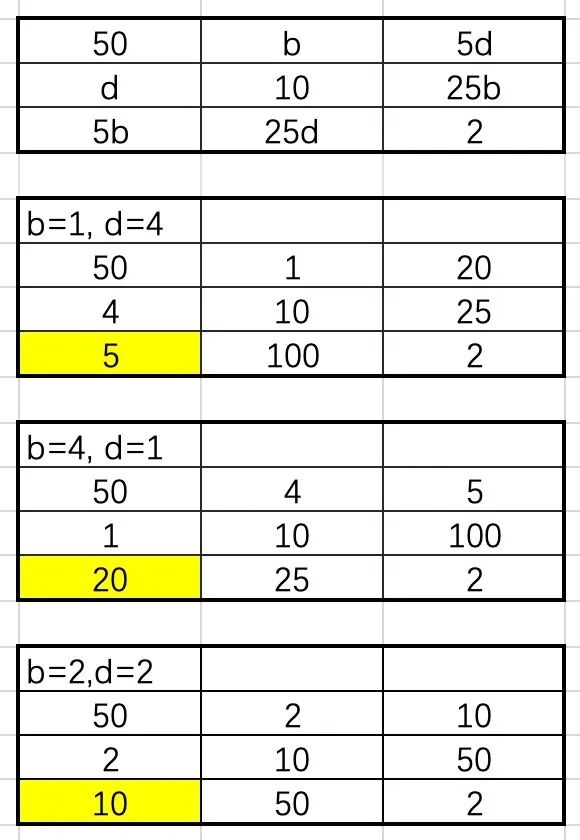
50*1*20

4*10*25

5*100*2

小明同学漏了一个解。

基于对称性的考虑，我们可以让右上角和左下角对调，再相应调整，可以得到下面的答案：

50*4*5

1*10*100

20*25*2

这个操作让人联想到办公软件excel的转置：行和列的转化。

评论区留言给出了一个漂亮的解答图：

先说答案：g=5或10或20三种结果，以下过程与式子： ①df=100 ② cg=100 ③ bh=100 ④bc=2e ⑤ dg=2e ⑥ gh=50e ⑦ cf=50e

②/⑤ c/d =50/e; ⑦/① c/d=e/2，得e=10（e∈N）

① df=100 ② cg=100 ③ bh=100 ④ bc=20 ⑤ dg=20 ⑥ gh=500 ⑦ cf=500

得：c=5d, f=25b, g=5b,h=25d; db=4;

科学尚未普及，媒体还需努力。感谢阅读，再见。