
你的供应商把你要的流程能力图(process capability charts)发过来了。图做得相当漂亮,一看就是用什么高级软件生成的——各种统计指标一应俱全,比如 Cpk、Ppk、σ水准(sigma level)、超出规格的ppm 等等。图好看得很,看起来你的供应商简直棒极了。你注意到其中一张能力图上,Ppk = 1.14,而 Cpk = 2.07。这俩为什么不一样?算了,不重要。反正 Cpk 大于 1.33,正好是你当初要求供应商达到的。那好,换个事情干吧。
你刚刚,错过了一个关于供应商品质表现(performance)的非常关键信息。知道是什么吗?
Cpk 和 Ppk 是衡量流程能力(process capability)的两个常用指标——也就是你的流程满足顾客规格要求的程度。现在的软件(software)很方便,只要把数据一丢进去,结果唰地就出来了。但很多时候,我们拿到这些结果,就直接往前走了,根本没仔细想过它们真正代表什么。本期优 思学院就来深入聊聊 Cpk 和 Ppk:它们是什么?它们在测什么?这些数值到底意味着什么?你该更相信哪一个?有些答案,可能会出乎你的意料。
流程能力回顾(Process Capability Review)流程能力分析(process capability analysis)要回答的问题是:你的流程在多大程度上满足规格——不管是顾客给的规格,还是你内部自定的规格。要计算流程能力,你需要三样东西:
- 流程平均值的估计值- 流程标准差(standard deviation)的估计值- 规格限(specification limits)

算 Cpk 和 Ppk 都是这三样,我们这里假设数据服从正态分布(normal distribution)。
流程能力指数(process capability indices)可以理解成一个比值:从流程平均值到某个规格限的距离,与流程“自然变差”的比。这里流程的自然变差通常取 3 倍流程标准差。图1 给出了基于上规格限(USL)计算流程能力指数的一般示意,其中 s 是流程变差的度量。
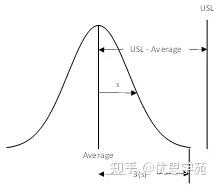
流程能力指数:
流程能力指数 = (USL – 平均值)/(3s)
要算流程能力,你必须能“合理地”估计流程平均值和流程标准差。注意,这不只是做个公式计算那么简单。这两个统计量必须是“有效的”(valid),后面我们会展开说。
Cpk 和 Ppk 回顾(Cpk and Ppk Review)Cpk 和 Ppk 都是“两个能力指数中的较小值”。它们的公式如下:

Cpk = min{ (USL − X̿)/(3σ), (X̿ − LSL)/(3σ) }Ppk = min{ (USL − X̿)/(3s), (X̿ − LSL)/(3s) }
这里 X̿ 是整体平均值(overall average)。
在 Cpk 的公式里,用 σ 来估计流程变差,这个 σ 是用极差控制图(R 控制图)估算出来的流程标准差(standard deviation estimate)。在 Ppk 的公式里,用 s 来估计流程变差,这个 s 是用全部数据直接算出来的标准差。
所以,Cpk 和 Ppk 的根本差别,就是“流程变差”的估计方式不一样。那这两种变差估计,差在哪里呢?
组内变差 vs 整体变差Cpk vs Ppk 的问题,本质上就是:组内变差(within subgroup variation, σ)和整体变差(overall variation, s)之间的差异。
先看整体标准差 s,它的公式是:
s = √[ Σ (Xi − X̿)² / (N − 1) ]
N 是全部数据点的个数。看根号下面那个求和项,就是把每个单个数据点和整体平均值的差值平方后加起来(见图2)。
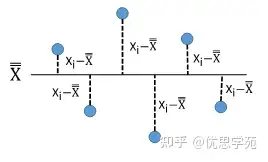
从公式的含义看,你可以把 s 理解为:每个数据点“平均离整体均值有多远”。由于计算时用到了所有数据,所以这个标准差 s 有时也叫整体变差(overall variation)——它把数据里存在的所有变差都算进去了。
现在我们看 σ,也就是通常说的组内变差(within subgroup variation)。这个 σ 是从极差控制图(range control chart)估出来的流程标准差。
比如,你用的是 X̅-R 控制图,子组(subgroup)大小为5。每次抽 5 个样本,这 5 个点的平均值就是 X̅,画在 X̅ 图上;这 5 个点的极差 R = 最大值 − 最小值,画在 R 图上(见图3)。R 就是这个亚组内部的变差度量。
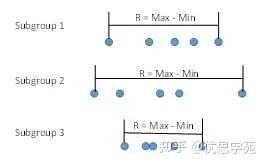
然后用下面这个公式估计 σ:
σ = R̅ / d₂
其中 R̅ 是平均极差,d₂ 是与亚组大小有关的控制图常数。所以 σ 只反映“组内”变差。它是否包含了全部变差,要看流程状态,后面会看到。
那个“小问题”:统计控制!(That Little Issue of Statistical Control!)
我们之前所有关于流程能力的文章,都一再强调一个前提:流程必须处于统计控制状态(in statistical control)。现实中,这个前提经常被完全忽略。
较早之前,优思学院六西格玛课程中提出的“流程能力检查清单”,用来帮你把流程能力的真实情况说清楚。清单有五项:
1)先用控制图(control chart)把数据画出来,判断流程是否处于统计控制状态(是否一致、可预测);2)对处于统计控制状态的流程,画直方图(histogram),并在图上加上规格限;3)对处于统计控制状态的流程,计算流程数据的自然变差;4)对处于统计控制状态的流程,计算 Cp 和 Cpk;5)把以上四项结果组合起来一起展示,用来说明流程能力。
你注意到了吗?“对于处于统计控制状态的流程”这句话出现了多少次?意思很简单:只要流程不在统计控制状态,Cpk(以及 Ppk)这些数值就没有意义。
关键点来了:如果你的流程处于统计控制状态,那么 Cpk 和 Ppk 的数值会非常接近。实际上,你可以用下面的经验来判断:
如果 Cpk ≈ Ppk,则流程在统计控制状态;如果 Cpk 和 Ppk 差别很大,则流程不在统计控制状态。
所以,当你看到供应商给你的图里,Cpk 和 Ppk 差得很大,其实你已经被“提醒”了一件事:供应商的流程不在统计控制状态——你拿到的未来产品会是什么样子,并不靠谱。
同样,如果流程不在统计控制状态,Cpk 和 Ppk 就基本没什么意义了。因为流程不一致、不稳定,你不能指望未来再得到类似的值。下面我们会通过一个例子进一步说明:两个流程用的是同一批数据,只是顺序不同。
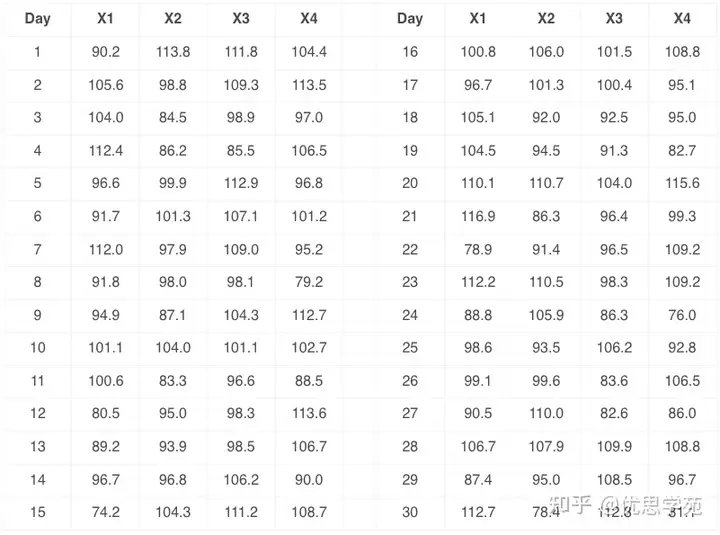
两个流程——同一批数据,同一个 Ppk我们来看两个流程(Process 1 和 Process 2),它们的数据来源完全一样(数据取自上一期文章),只是排序不同。假设你每小时取 4 个样本,组成一个亚组。你想判断这个流程能否满足规格要求:LSL = 65,USL = 145。流程1的 30 个亚组数据见表2(略)。
流程2的数据和流程1是同一批,只是顺序完全打乱了一下,见表3(略)。
由于本质上是同一批数据,所以表2和表3的数据有同样的平均值和同样的标准差:
平均值 = 98.98标准差 s = 9.89
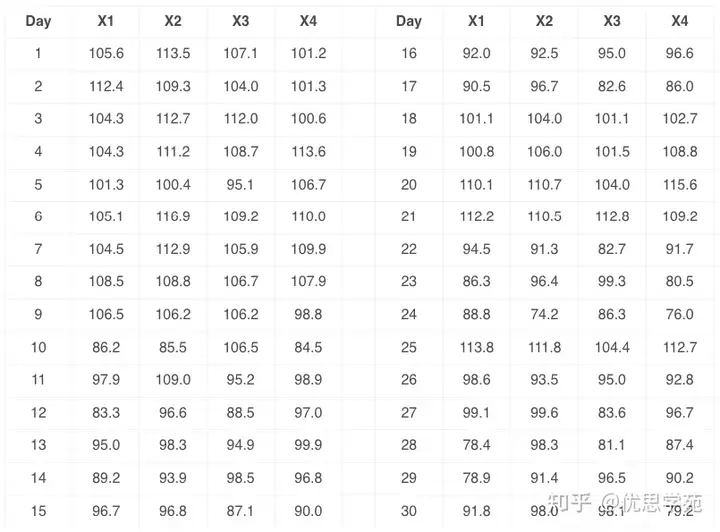
现在你用表2的数据画一个直方图,用表3的数据再画一个直方图,然后加上规格限 LSL = 65,USL = 145。你会发现,两张直方图一模一样——这很正常,因为数据是完全相同的一套。图4就是这个直方图。
从图上看,这个流程表现很不错——整体分布完全在规格范围里。你当然很满意。接下来,你计算流程1和流程2的 Ppk。由于均值和标准差完全一样,两个流程的 Ppk 也必然一样。计算如下:

所以,流程1和流程2的 Ppk 都是 1.14。
两个流程——同一批数据,不同的 Cpk等等,那 Cpk 呢?两个流程的 Cpk 一样不一样?答案:不一样。
记住,Cpk 是基于组内变差(within subgroup variation)算出来的。虽然两套数据本质上相同,但亚组的“分组顺序”不一样,就会导致“组内变差”不同。
算 Cpk 时,你需要通过 R 控制图估算标准差 σ,并通过 X̅ 控制图估算整体平均值。注意,这是 Ppk 和 Cpk 之间一个非常重要的区别:Ppk 只是对所有数据直接做计算;Cpk 是通过控制图来估算平均值和流程变差——这是一种“用于预判未来”的方法。
先看流程1。流程1的 R 图如图5所示。
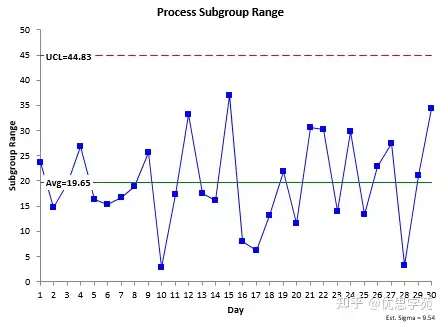
R 图处于统计控制状态,说明组内变差是稳定、一致、可预测的。于是你可以通过下面公式估计标准差:
σ = R̅ / d₂ = 22.50 / 2.357 = 9.54(约)
因为 R 图在统计控制状态,所以基于组内变差得到的 σ 是“有效的”:产生这些数据的流程是一致、可预测的,只要流程不变,未来也会保持这种水平。
接下来算 Cpk 还需要一个流程平均值,这个来自 X̅ 控制图。流程1的 X̅ 图如图6所示。
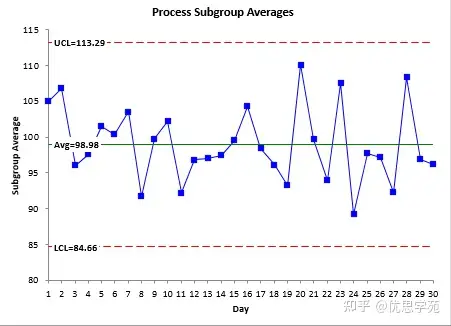
X̅ 图也处于统计控制状态,说明你对流程平均值的估计是可靠的“有效”估计。于是你可以用这个平均值和 σ 来算 Cpk:
Cpu = (USL − X̿)/(3σ) = (145 − 98.98)/(3×9.54) = 1.61Cpl = (X̿ − LSL)/(3σ) = (98.98 − 65)/(3×9.54) = 1.19Cpk = min{Cpu, Cpl} = 1.19
现在比较一下流程1的 Ppk 和 Cpk:
流程1:Ppks = 9.89Ppu = 1.55Ppl = 1.14Ppk = 1.14
流程1:Cpkσ = 9.54Cpu = 1.61Cpl = 1.19Cpk = 1.19
你会发现两套结果非常接近。只要流程在统计控制状态,情况总是这样——因为:
当流程处于统计控制状态时,组内变差是整体变差的一个好估计,也就是说 σ ≈ s;在这种情况下,Cpk 基本等同于 Ppk,它们在讲同一件事。
现在看流程2。流程2的 R 图如图7所示。
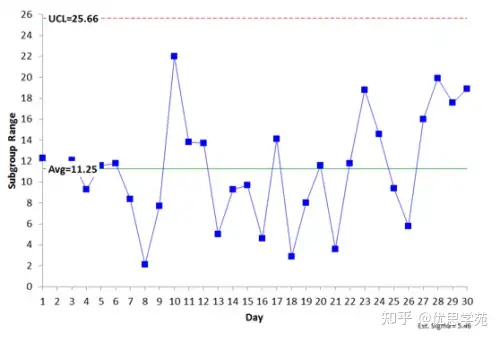
R 图同样处于统计控制状态——也就是说组内变差稳定、可预测。于是可以估计标准差:
σ = R̅ / d₂ = 12.87 / 2.357 = 5.46(约)
接下来算 Cpk,仍然需要整体平均值 X̿,这个要从 X̅ 控制图来。流程2的 X̅ 图如图8所示。
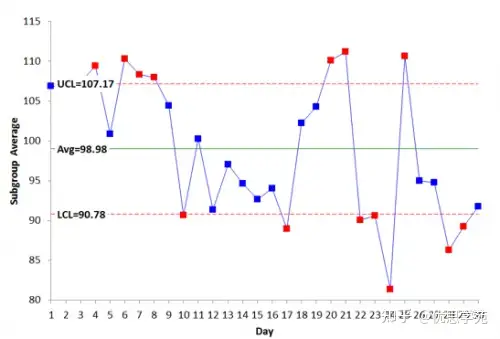
但这一次,X̅ 图不在统计控制状态:有点超出控制限,有长串点都在平均线一侧,等等。总之,流程“亚组间”的变差不稳定、不可预测。
这意味着,你对流程平均值并没有一个“靠谱”的估计。均值在来回飘,你根本说不准下一组的平均值会到哪里。流程不一致、不稳定,所以从未来角度看,你其实“没法”算一个有意义的 Cpk。
但在实际工作中,很多人对这一点直接视而不见,还是照样硬算 Cpk。反正算出来的平均值也是 98.98。于是按公式算:
Cpu = (USL − X̿)/(3σ) = (145 − 98.98)/(3×5.46) = 2.81Cpl = (X̿ − LSL)/(3σ) = (98.98 − 65)/(3×5.46) = 2.07Cpk = min{Cpu, Cpl} = 2.07
这就得到流程2的 Cpk = 2.07。现在把流程1和流程2的结果并排比较一下:
流程1 & 流程2:Ppk(相同数据)s = 9.89Ppu = 1.55Ppl = 1.14Ppk = 1.14
流程1:Cpkσ = 9.54Cpu = 1.61Cpl = 1.19Cpk = 1.19
流程2:Cpkσ = 5.46Cpu = 2.81Cpl = 2.07Cpk = 2.07
可以看到,流程2 的 Cpu、Cpl 与 Ppu、Ppl 差别非常大。归根到底,就是统计控制的问题:当 σ 和 s 差距很大时,Cpu 与 Ppu、Cpl 与 Ppl 之间差距也会很大——这强烈暗示流程不在统计控制状态。
总结:到底谁更“靠谱”:Cpk 还是 Ppk?现实中,Cpk 更适合用来评估流程“潜在能达到的水平”(potential capability)。它代表在“理想状态下”你的流程能做到多好——所谓理想状态,就是组内变差和组间变差基本一样,也就是流程处于统计控制状态。
当流程处于统计控制状态时,Cpk 和 Ppk 基本相等,因此这时候其实不太需要 Ppk,多看 Cpk 就够了。
而如果流程不在统计控制状态,那你真正该干的事,是先让流程“稳定下来”,而不是纠结 Cpk 或 Ppk 的数值高低。此时这两个数值大体上都没什么实际意义——唯一有用的信息就是:如果 Cpk 和 Ppk 差很多,那八成说明流程不稳定、不受控。
不过说实话,你本来就应该知道这些,因为你在用优思 学院的流程能力检查清单。任何关于流程能力的分析,都应该从控制图开始——先看看数据是不是在统计控制状态。只有在这个前提下,谈 Cp、Cpk、Ppk 才有意义。