高中学了平面向量基本定理后,教辅资料有这样一道习题。
题目呈现如下图所示:

空白处在等待读者的答案
如果不考虑向量法,这道题目对初中同学来说,那是轻松拿捏。
问题来了,这道题用高中的向量法该如何解题呢?
读者可能离开学校很久了,高中数学知识忘记了。不过不用担心,我们来看看张景中先生如何解题,让人受益匪浅。在读后感部分,为读者准备了知识概括,帮助大家回忆高中学过的平面向量的相关知识点。
接下来请看张景中先生解一道类似的题目。

接下来的例5在综合几何中,本是一道极常见的题目,根本不值得一提,随便找一个学过三角形相似的初中生就轻松做出来,但就是这样一道题,却在高中的向量教学中,掀起了波澜。多个版本的高中数学教材都选用了此题,或作例题或为习题。
【例5】如图4,在平行四边形 ABCD 中 E 和 F 分别为 AD和 CD 中点,连接 BE 和 BF 交 AC 于点 R 和 T ,求证 R 和 T 分别为 AC 的三等分点。

证明
第一步,建立平面几何与向量的关系,用向量表示问题中的几何元素,将平面几何问题转化成向量问题:设 AB = a , AD = b , AR = r , AT = t ,则 AC = a + b .
第二步,通过向量运算,研究几何元素之间的关系:由于 AR 与 AC 共线,所以,我们设 r = n ( a + b ), n∈R ,又因为......
第三步,把运算结果"翻译"成几何关系: AR = RT = TC .以上证明抄自某教材,未作改动。
初中生很容易解答的题目(易证△ATB∽△CTF,从而AT:CT =AB:CF=2),到了高中反而越来越复杂了,教科书直接影响了教师的思维,一位老师专门对此题作了探究,发表的文章中总结了5种解法,都较烦琐。这样的向量法证明给不少老师带来了疑惑,他们在教学中不知道如何向学生解释课标中所谓的"向量法的先进性"!
能否利用向量法非常简单地证明此题呢?证法是有的,另证:由题意得(向量的上标箭头打不出来) AT + TB = AB = DC =2FC=2FT+2TC.根据平面向量基本定理得 AT =2 TC ,故点 T 为 AC 的三等分点,同理点 R 为 AC 的三等分点。
此证法的思路体现了前述处理交点问题的诀窍:从涉及解题目标 AT(上标箭头打字打不出来,下同) 的回路等式 AT + TB = AB 出发,把其中不在相交线段上的向量 AB 化到相交线段上,问题就解决了。
从这可看出,不是向量法本身有问题,而是没有正确使用向量法来解题,向量具有几何形式和代数形式的"双重身份",这也是将向量引入中学教材的一个重要原因,若不能超脱坐标情结和方程情结,过于注重其代数形式,忽视了几何形式,以致运用向量法解题时,与代数中的解应用题方法(设未知数,列方程)基本相同,将几何问题转化为方程组求解,其中包括大量运算,自然较为烦琐。
一些资料将向量解题总结为"三部曲":①向量表示(把几何问题中的点、直线、平面等元素用向量表示);②向量运算(针对几何问题,进行向量运算);③回归几何(对向量运算结果作出几何意义上的解释).
这一总结是一个大的指导方针,从理论上来说,是没有问题的,上面诸例中简洁的向量解法,仔细分析起来无非也是这"三部曲",在实际操作的时候,无需死守套路,完全可以根据几何意义列出等式,计算与图形融为一体;关键之处就在于领会向量几何,其运算不仅仅是数的运算,还包括图形的运算,这是向量法解题的特点,而把向量化到相交线段上,实质也是在寻求一对有效的坐标标架,
正如陈昌平、张奠宙等诸位先生所说:向量和几何的融合,已是不可阻挡的潮流,向量解题引入教材,是必然,也是好事;一方面能够使很多的知识贯穿起来,成为系列;另一方面也有利于学生进一步学习高等数学,
但从目前的情况来看,如何编写向量法的教材,如何进行向量法的教学和解题,还很值得研究,单墫教授认为,同一个数学问题的不同解法,可以有美丑之分,简洁明快是一种数学美,在数学解题教学中,当然应当引导学生寻求更美的解题方法,从上面的例子看,向量解题方法朝着更美的目标的提升,还有很大空间,何时这空间变得狭窄了,教材上期刊上这些烦琐的解题方法稀少了,老师、学生们对向量解题的优越性心服口服了,本书也就无用了。
多数作者希望写出不朽的作品,笔者却愿本书速朽,
本书题目很多,收集、整理、排列,虽费了不少工夫,仍不敢说没有错漏之处,欢迎来信批评指正。
2010年6月
张景中
以上引自《绕来绕去的向量法》一书的前言(节选),作者是张景中。
读后感
平面向量的知识概括
已知非零向量a,b,在平面内取任意一点A,作
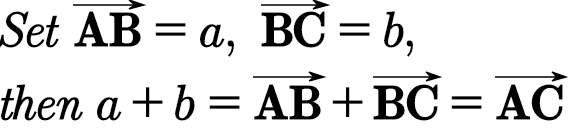
求两个向量和的运算,叫做向量的加法。这种求向量和的方法,称为向量加法的三角形法则。归纳口诀为:“首尾相连连首尾”。
此外,还有向量加法的平行四边形法则。
相反向量:与向量a长度相等,方向相反的向量,叫做a的相反向量,记作-a。
向量的减法:向量a加上b的相反向量,叫做a与b的差,即
a-b=a+(-b),求两个向量差的运算叫做向量的减法。
从定义可看出,向量的减法可以转化成向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。
已知向量a,b,在平面内任取一点O,作
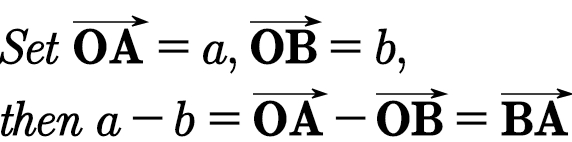
即a-b可以表示为从向量b的终点指向向量a的终点的向量,这就是向量减法的几何意义。归纳口诀为:共起点、连终点、指被减,意思是求两个向量的差向量时,起点要重合,连接它们的终点,方向由减向量的终点指向被减向量的终点。




例5如果用几何法解题,还有一种解法:使用共边定理。
解题过程请看下图:

共边定理可以让面积比和线段比相互转化,轻松解题。
科学尚未普及,媒体还需努力。感谢阅读,再见。