
使用全新的meta psycorr命令执行心理测量学meta分析。该命令可整合测量误差、范围限制等因素的校正相关系数。此功能现在是StataNow的一部分。
Meta分析通常侧重于比较两个不同组之间的二元或连续结果(新药vs安慰剂,或教学方法A vs教学方法B)。它是汇总研究效应量的有力工具。
但如果您关注的是两个变量--例如工作满意度与员工绩效,或正念饮食与自我调节--在数十项研究中的关系呢?而且,如果这些变量无法直接观测,只能通过存在误差的工具或在有限的样本范围内进行测量,又该如何处理呢?这类挑战正是心理测量学meta分析旨在解决的问题。心理测量meta分析(Schmidt and Hunter 2015)并不仅仅是简单合并相关系数,更重要的是校正那些可能扭曲真相的统计假象。例如测量误差、范围限制、二分变量化以及小样本偏差。这些并非次要问题--当我们处理像智力、幸福感或动机这类潜变量时,它们恰恰是需要关注的核心问题。
Stata全新推出的meta psycorr命令让心理测量meta分析变得简单直接。通过该命令,您可以轻松计算校正后的相关系数与标准误,并将数据集声明为适用于全套meta分析流程的标准化数据,为后续深度分析做好准备。应用示例
正念饮食能否重塑您的自控力?由于您对相关性的meta分析(MA),鹰嘴豆肉饼和其他豆类菜品大受欢迎。您未来的婆婆则把目标定得更高:写一本关于正念饮食的书。但她决心以科学为依据,而不是猜测。她在健康界听到一些传言,有意识的饮食(慢慢吃,不受干扰,听饥饿和饱腹感的暗示)可能与提高自我控制能力(调节冲动和专注于长期目标而不是短期诱惑的能力)、降低BMI甚至减少焦虑有关。她想知道以下问题:是否有确凿证据表明用心饮食确实与更好的心理状态相关?了解数据和研究结果
您收集了13项研究来测量正念饮食(T)与自我控制(P)之间的相关性。
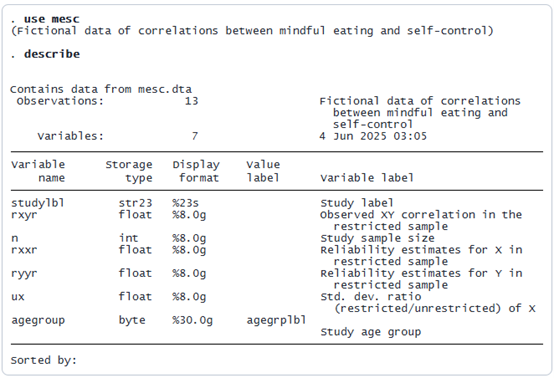
变量 T 与 P 属于潜在变量,无法直接测量。现有研究采用问卷调查中针对 T 和 P 设计的题项进行测量,但这些变量的测量过程存在误差。分别使用工具(问卷得分)x和y测量T和P的可靠性估计值存储在变量rxxr和ryyr中。但问题不止于此。研究参与者并非随机选取。各项实验的样本均来自特定受限群体--这些个体是根据一个综合了年龄、性别、健康意识与整体动机的潜在适配度变量(暂称为 s)筛选出来的。虽然变量 s 无法直接观测,但其影响显而易见:参与者是通过非随机筛选机制进入样本的。事实上,这种筛选很可能分两个阶段进行:1. 首先,有更多的参与者进入了研究流程(例如,申请、招募或完成了初步调查)。这构成了未受限制的样本。2. 最终基于变量 s 从该群体中筛选出的受限样本,不仅降低了正念饮食得分(x)的变异性,也扭曲了观测到的相关关系。这正是间接范围限制的典型案例。在完全中介假设下--即假设筛选(基于变量s)对结果变量(自控力)的影响完全通过预测变量(正念饮食)传递--我们可以对此偏差进行单变量校正。之所以称为“单变量”校正,是因为它只需要知道相关系数中两个变量之一(预测变量或结果变量)的u比率信息。u比率(存储在变量ux中)是指受限样本中 x的标准差与无限制样本中x标准差的比值。当该比值小于1时,表明由于筛选导致x的变异性降低,从而使观测到的相关系数衰减--这意味着受限样本中x与y的相关系数(存储在变量rxyr中)将小于无限制样本中的真实相关系数。校正测量误差和范围限制现在我们可以使用meta psycorr来校正测量误差和间接范围限制,其中变量n和studylbl分别代表研究样本量和标签:
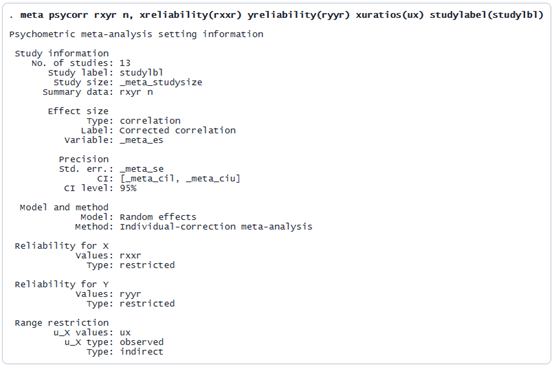
简而言之,meta psycorr报告称,我们正在使用随机效应模型对13项研究进行个体校正的MA分析。我们为两个变量(来自受限样本)指定了可靠性估计值,并假设存在间接范围限制,为x提供了u比率。Stata利用这些信息来校正观测到的相关性以消除测量误差和范围限制,并计算其标准误差,分别将结果存储在_meta_es和_meta_se中。探索备选设置方案我们此前默认范围限制为间接类型(这是实践中最常见的假设),但为便于演示,若需假设其为直接范围限制(例如筛选直接基于变量x执行)并保持其他所有设置不变,则可通过meta update命令进行调整。
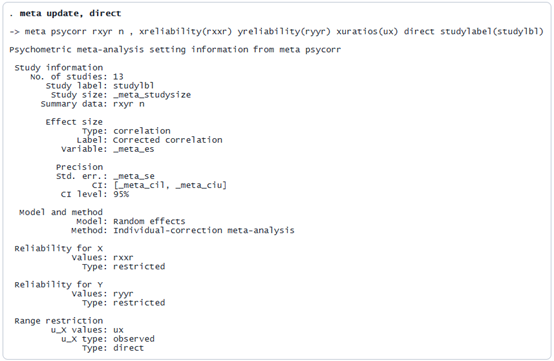
或者,如果您希望假设可靠性估计值来自未受限制的样本,并存储在变量rxxu中,则输入

关于统计结果的其他信息说明示例,请参见[META] meta psycorr中的示例2至6。Meta分析总结与可视化结果继续使用我们对meta psycorr的第一个设定,让我们总结meta分析结果,计算总体(平均)校正相关系数,并使用选项credinterval选项显示80%(默认)可信区间。

输出表头列出了用于校正相关性衰减所使用的各项指标。输出表的第二列显示了单独校正的相关性而第三列和第四列显示了相应的95%置信区间(CI)。平均校正相关系数为0.518,95%置信区间为[0.406, 0.631]。我们还可以展示心理测量meta分析的结果,并通过森林图以图形方式显示可信区间。
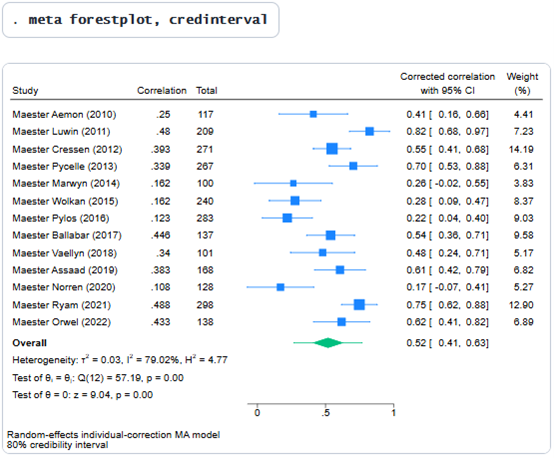
图中绿色菱形即总体效应量,其中心对应平均校正相关系数估计值。菱形的宽度对应于总体置信区间 [0.41, 0.63] 的宽度。从总体菱形延伸出的绿色须状线,其跨度为meta summarize中显示的可信区间 [0.269, 0.768] 的宽度。其他统计假象及双变量范围限制建模您可以校正的其他统计假象包括小样本偏差以及变量x与y得分的二分处理。当完全中介假设不成立时,您仍可不依赖该假设对间接范围限制进行校正,但这需要掌握受限群体与无限制群体中y变量的标准差比率信息。由于该方法需要同时获取x与y的u 比率,Wiernik 和 Dahlke(2020)将其称为双变量间接范围限制校正法。例如,若需执行BVIRR校正,您可输入以下命令:

亚组meta分析**亚组元分析**
您的岳母很好奇:正念饮食与自控力的关联在不同群体中是否存在差异?例如,老年人群体与年轻人群体的关联强度是否不同?
您可以根据agegroup变量拆分数据集,并生成各亚组专属的森林图:
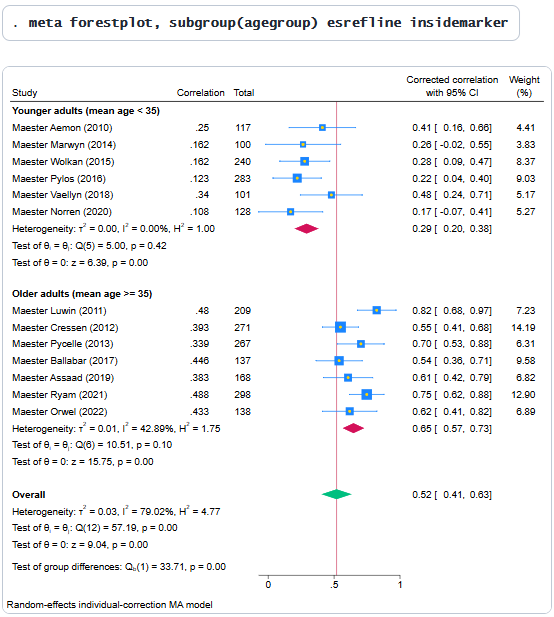
您会发现,老年人表现出更强的校正相关性(0.65 对比 0.29)--这一结果与晚年自我调节能力增强以及生活规律更健康的相关理论相符。心理测量学meta分析表面:正念饮食与自控力确实密切相关--对我们当中的阅历丰富者而言尤其如此。