读读欧拉吧，他是我们所有人的老师！作者：原本1024代数的定义出奇的简单——“用已知求未知”：现代教科书可能会用函数、集合、运算等概念来定义代数，但欧拉的定义却直击要害，在他看来，代数的本质可以被浓缩为一句简单的话：

这门科学教我们如何通过已知量来确定未知量。 (The science which teaches how to determine unknown quantities by means of those that are known.)，它将代数从一门“关于规则的学科“转变为一种“解决问题的思维方式”，学习代数的目的不是背诵公式，而是掌握一种从已知信息中推导出未知答案的逻辑艺术。

这个简单的定义，是理解代数所有后续内容的基础。

代数解题中最难的部分是什么？很多人会说是计算，但真正的难点在于“翻译”——将日常语言描述的问题，准确地转换成数学语言。让我们看看欧拉是如何解决这个问题的：

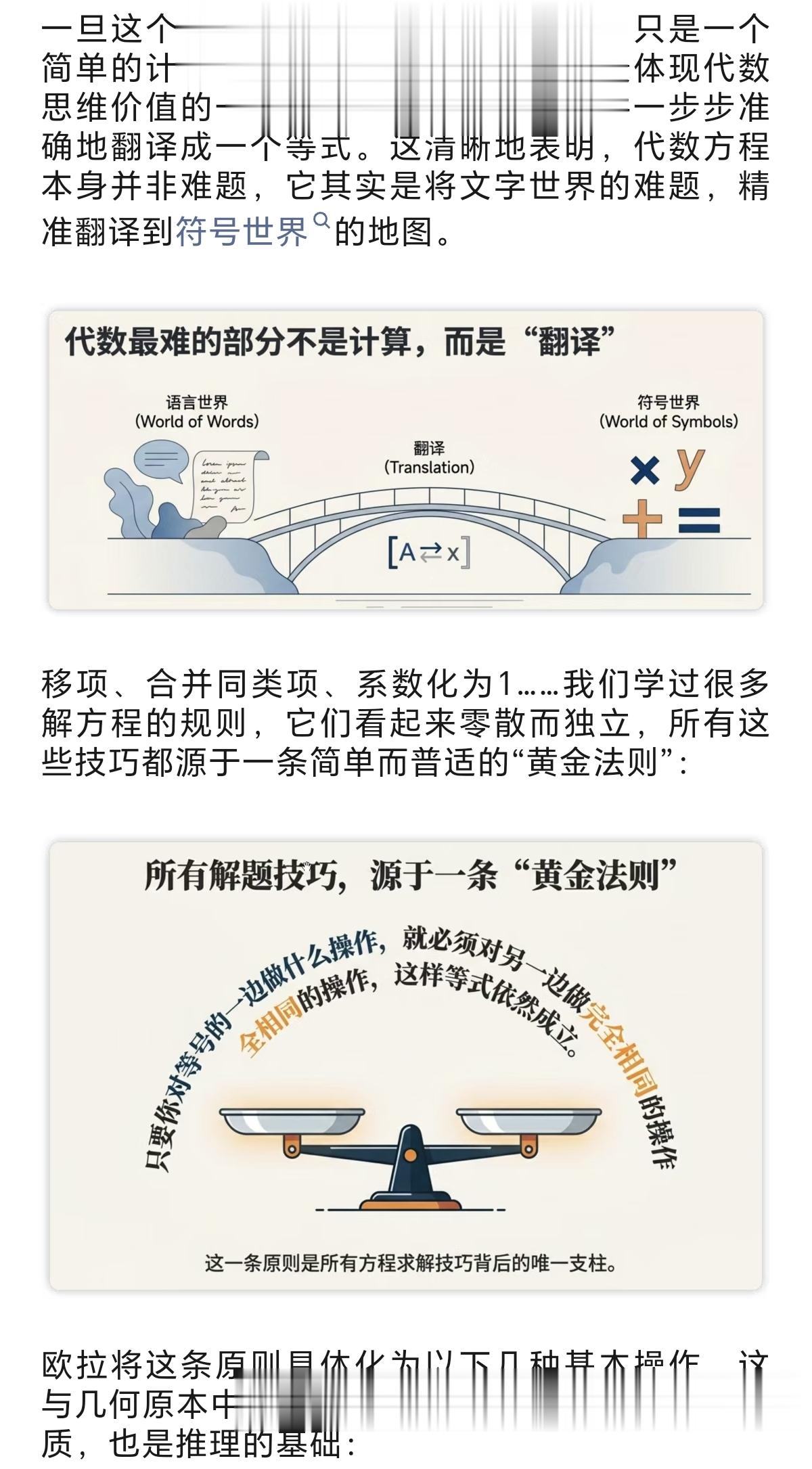
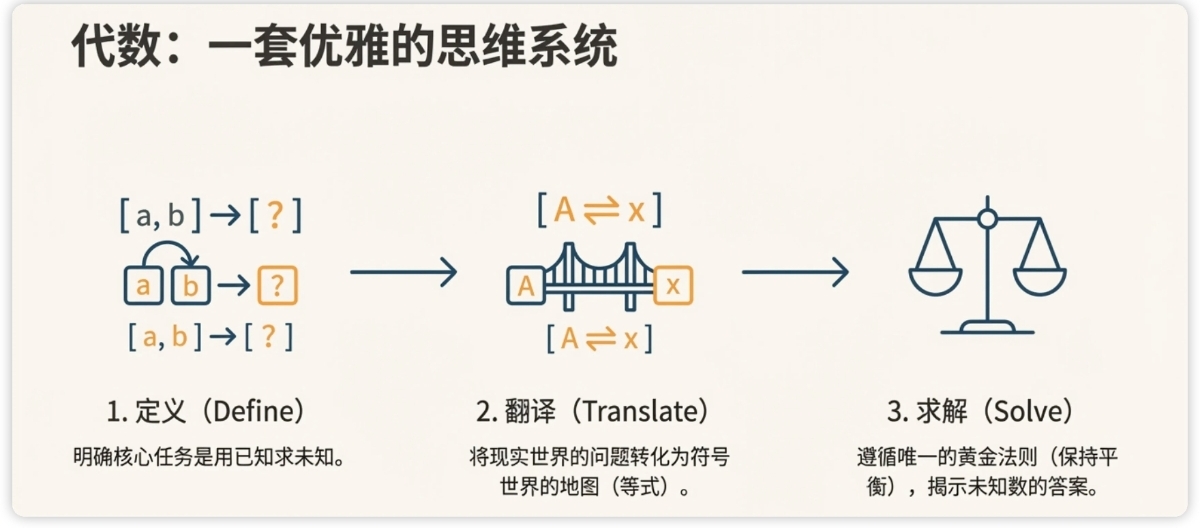
再看一道例题。

稍后我们讨论怎么解分式方程。

读后感

分母含有未知数的方程是分式方程。解分式方程需要考虑如何化为整式方程。

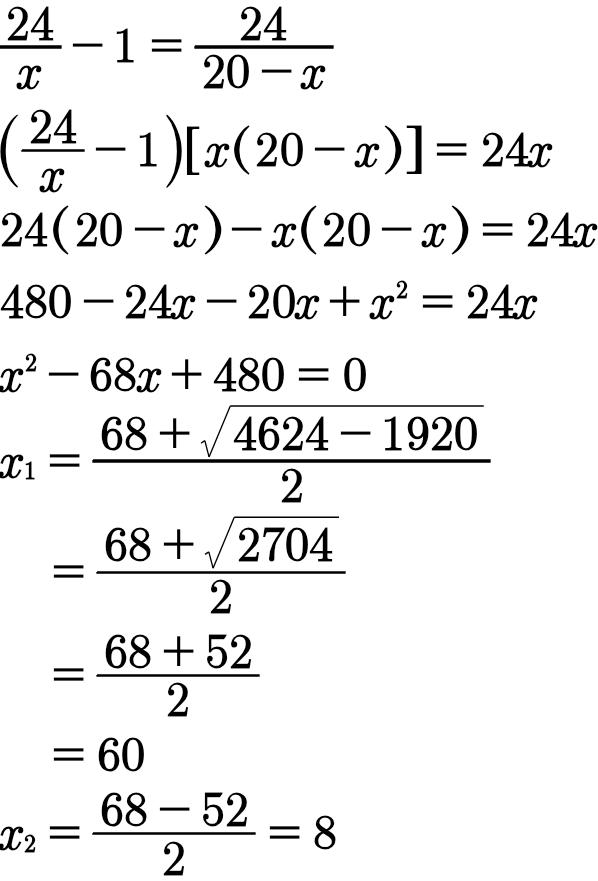
去分母后我们得到一个一元二次方程。运用求根公式我们得到两个根：x=60或x=8。

因为x=60不合题意，故舍弃。

最后得到答案：x=8。

但是等等，还有更好的解法。

初中同学学习了一个乘法公式：

(x+a)(x+b)=x²+(a+b)x+ab

这个公式从左到右是乘法公式，反过来，从右往左则是因式分解公式。

故得到，

(x-60)(x-8)=x²-68x+480

所以，方程的两个根是60或8。

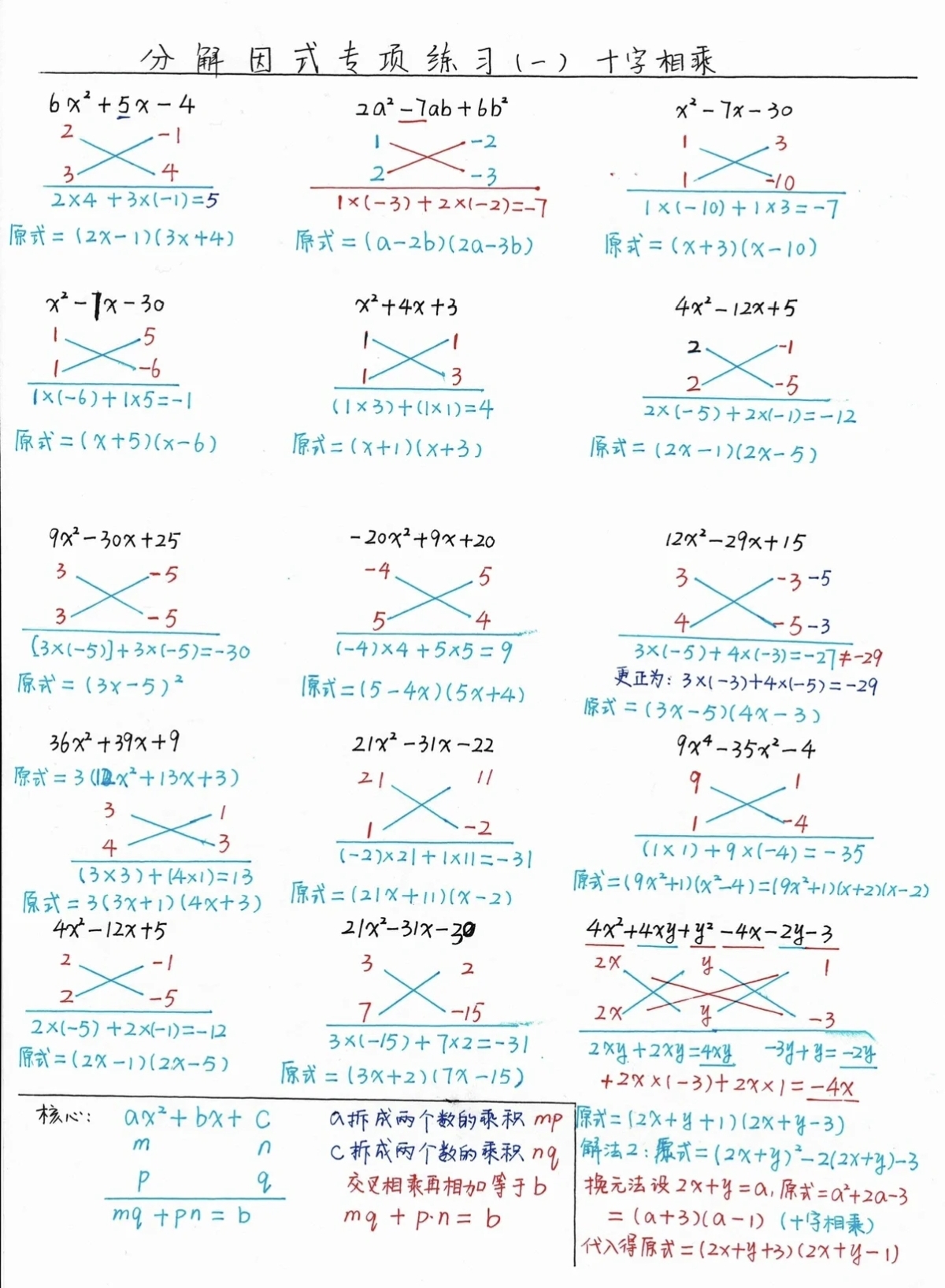
十字相乘法可以帮助我们分解因式。

科学尚未普及，媒体还需努力。感谢阅读，再见。