在数学中，寻找平铺平面（tiling）的瓷砖已经有相当长的历史。平铺平面是一个数学和几何概念，指的是使用一个或多个形状（称为“瓷砖”）来覆盖一个平面，而不留下任何间隙或重叠。这些瓷砖可以是规则的（如正方形、六边形等）或不规则的。

一个著名的平铺平面类型是“周期性平铺”，它由一个或多个形状组成，这些形状可以按照规律的方式无限次重复覆盖平面。另一种类型是“非周期性平铺”或“无规律平铺”，其中所使用的瓷砖可以填充整个平面，但不能形成重复的格局。非周期性平铺在数学和物理学中引起了特别的兴趣，因为它们与拓扑学、晶体学和准晶体结构等领域密切相关。

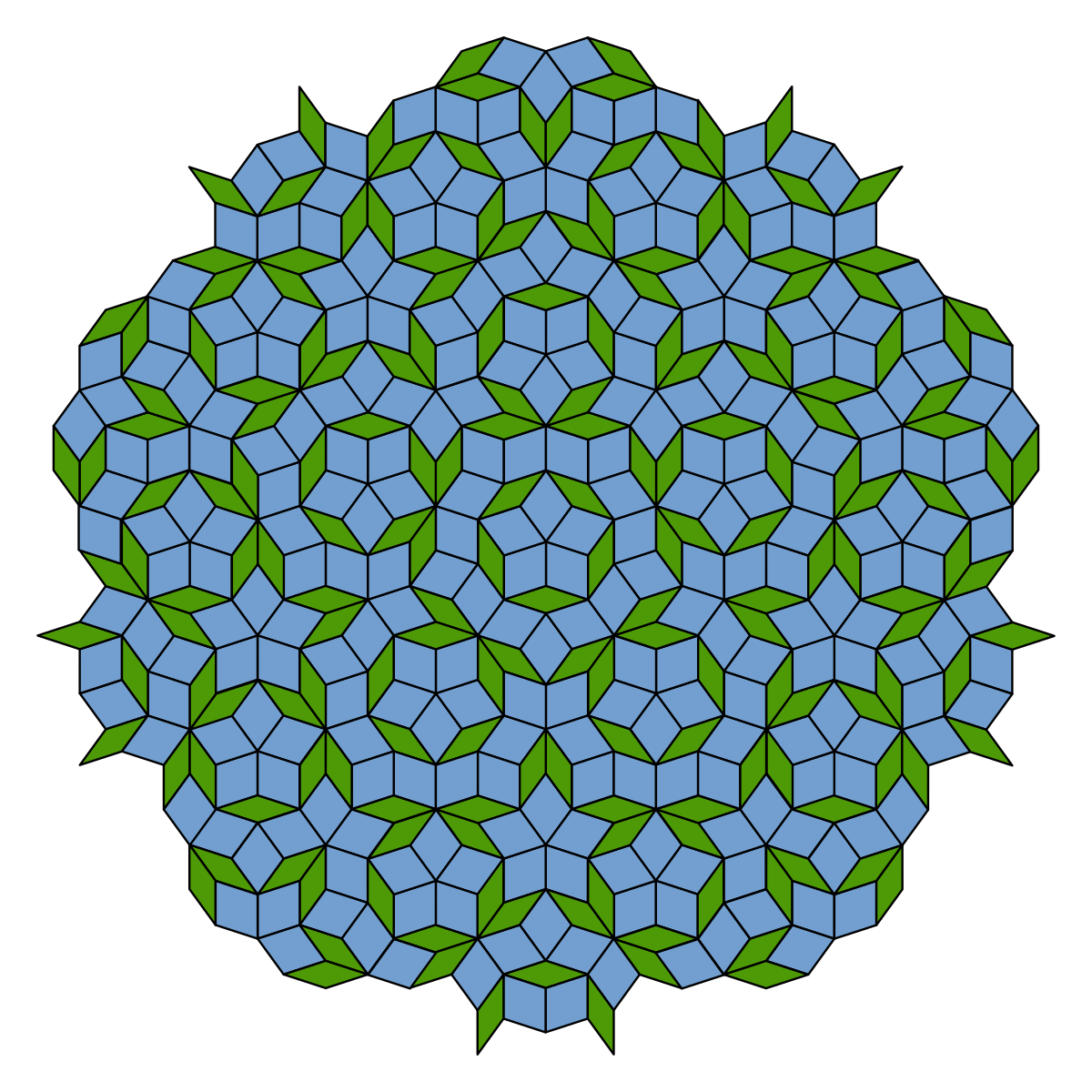
彭罗斯平铺（Penrose tiling）就是一种非周期性平铺，由英国数学家罗杰·彭罗斯（Roger Penrose）于20世纪70年代发现。彭罗斯平铺使用两种形状（通常称为P型和Q型瓷砖）覆盖平面，它们具有五边形对称性，但没有周期性排列方式。彭罗斯平铺具有许多独特和有趣的数学性质，例如它是非周期性的，但仍然是局部有序的。

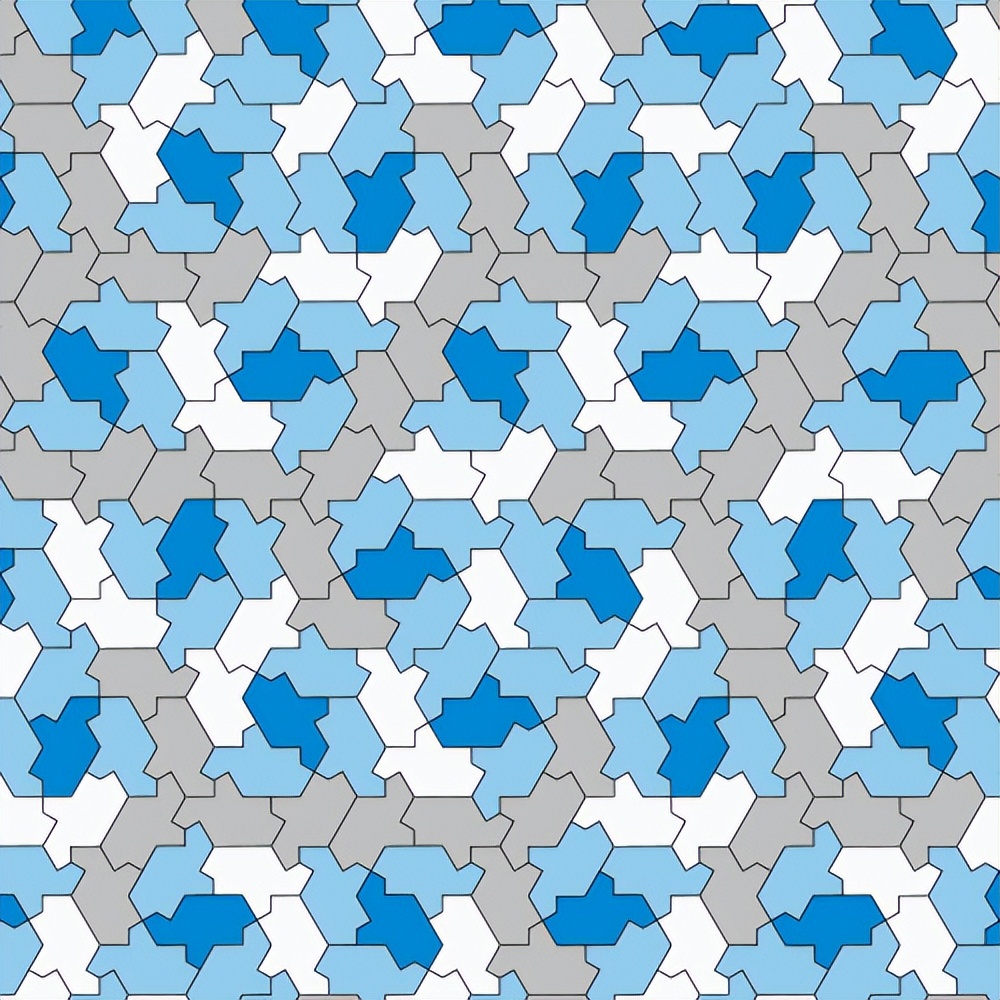
3月20日，英国业余数学爱好者约瑟夫·史密斯（Joseph Smith）发现了一个名为“帽子”的瓷砖，这个瓷砖不仅可以无缝覆盖平面，而且是非周期性的。研究人员在他们的论文中写道，帽子瓷砖体现了“足够的复杂性，强制性地在所有尺度上破坏周期性。更重要的是，帽子只是这类图块中无穷多个不同图块之一。

自上世纪90年代以来，数学家们一直在寻找一种单一的瓷砖，能够在没有间隙或重叠的情况下非周期性地填充二维平面。这种瓷砖被称为爱因斯坦瓷砖（Einstein tile）。这种形状被认为具有很高的数学价值，因为它挑战了我们对传统的平面铺砖模式的认知。

在90年代，两个研究团队找到了一种方法，将相邻的单个十边形瓷砖重叠在一起，实现了非周期性地覆盖平面。大约十年后，塔斯马尼亚的业余数学家琼·泰勒（Joan Taylor）发现了一个具有多个不连续部分的形状。她在2010年的一篇论文中证明了这种形状能够非周期性地铺满平面。就在去年，加州大学洛杉矶分校的陶哲轩（Terence Tao）发现了一种高维形状，它可以非周期性地铺满空间，甚至无需旋转或反射。然而，没有人能找到一个真正的“爱因斯坦瓷砖”。数学家们甚至怀疑这样的瓷砖是否存在。

帽子瓷砖（一种爱因斯坦瓷砖）到现在才被发现是有原因的。数学家们通常关注具有“禁忌”对称性的形状 —— 不能出现在周期性铺砖中的对称性。例如，彭罗斯瓷砖具有五重对称性（fivefold symmetries）。

五重对称性是指一个形状或图案在旋转180度之前能够重合五次。这种对称性在五边形和五角星中可以观察到。这种对称性是具有特殊意义的，因为具有五重对称性的形状（如常规五边形）无法平铺整个平面，这使得具有五重对称性的非周期性铺砖成为数学家关注的焦点。

相比之下，帽子瓷砖没有对称性。然而，它的铺砖与一种特定的周期性铺砖有着深刻的关系：六边形蜂窝格子。从六边形铺砖得到帽子铺砖的方法是首先连接六边形相对边的中点。这样可以将每个六边形划分为六个“风筝”。每个帽子由相邻六边形组合而成的八个相邻风筝组成。

帽子瓷砖表明周期性和非周期性瓷砖之间的联系比数学家们原先认识到的更为紧密。

对于所有可能的瓷砖组合，不可能创建一个算法来判断它们是否能铺满平面（更不用说它们是否是非周期性的了）。因此，从数学上讲，史密斯发现帽子瓷砖是非常不容易的。但与此同时，史密斯又发现了另一个看似非周期性的瓷砖，形状像一只乌龟。一月中旬，史密斯找来了两位平铺专家，仅仅用了一周多一点的时间，他们就证明了“乌龟”是非周期性的。连续发现两个爱因斯坦瓷砖（单瓷砖非周期平铺）令人难以置信。

他们的证明采用了贝尔格（Berger）在20世纪60年代提出的一种方法，该方法涉及将瓷砖拼接成更大版本的自身，从而创建出一种分层结构。首先，确定由帽子组成的四种中间形状，称为H、T、P和F。例如，H是由四个帽子拼接而成的，形成一个大致像削去尖端的三角形。研究表明，你可以将四种形状的组合拼接成更大的形状。例如，你可以通过用三个H包围一个T，然后用P和F的组合包围这个对象来制作更大的H。

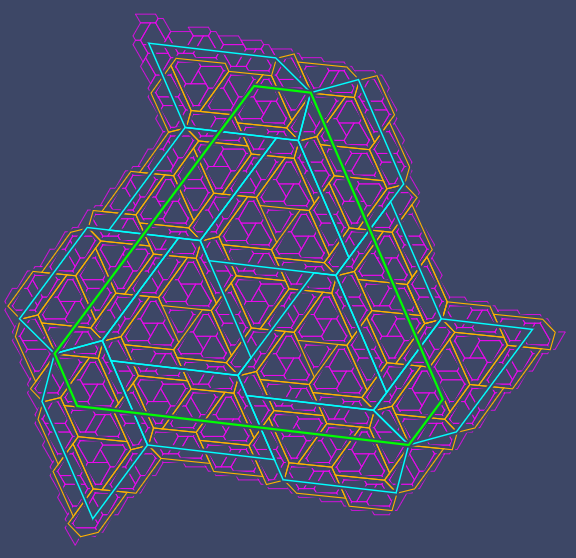
四个超级瓷砖还可以进一步排列成更大的超级瓷砖

这提供了一种制作越来越大的帽子铺砖的方法。你可以从一个H开始，增加它的大小，然后用上面四种形状的组合来填充它。你可以无限地重复这些步骤，在形状中构建越来越大的形状层次结构。但层次结构的最底层是“帽子”。

研究人员证明了这些分层结构所创建的铺砖永远不会是周期性的。他们还证明了分层结构是制作帽子铺砖的唯一方法。因此，帽子铺砖永远不会是周期性的。

另一个爱因斯坦瓷砖是上面提到的“乌龟”。帽子和乌龟铺砖看起来非常相似，研究人员怀疑乌龟也是非周期性的。但他们的怀疑并不是证据。

然后，研究人员意识到，帽子和乌龟属于一个无穷大的砖瓦家族，所有这些砖瓦都以相同的方式填充平面。

每个帽子有13个边：六个长边和六个与风筝边相对应的短边，再加上一个由两个短风筝边组成的边。通过改变“帽子”的边的相对长度，可以产生一个形状的连续统

物理学家已经开始探索这些铺砖的材料属性。他们发现，如果通过这些铺砖射出一束光，所产生的衍射图案具有研究人员在准晶体中观察到的同样类型的尖峰。