接上篇：傅里叶变换的强大，远超你的想象，深挖其背后的数学原理和细节

在数据科学、通信、图像处理以及许多其他领域，傅立叶变换（Fourier Transform）是一个重要的数学工具，它允许我们在时域和频域之间进行转换。然而，对于大规模数据的处理，传统的傅立叶变换可能会非常耗时，这在实际应用中会变得不可接受。此时，快速傅立叶变换（Fast Fourier Transform，FFT）就显得非常重要。

快速傅立叶变换，简称FFT，是一种高效的算法，它能够快速计算傅立叶变换和其逆变换。FFT利用了傅立叶变换的一些数学性质，使得其计算效率大大提高。这一突破性的算法首次被Cooley和Tukey在1965年公开介绍，但其基本思想可以追溯到高斯在1805年的工作。

尽管FFT与傅立叶变换在数学上是等价的，但由于其在计算效率上的优势，FFT已经成为了实际计算傅立叶变换的主要工具。通过减少计算的复杂性，FFT使得实时处理大量数据成为可能，这无疑极大地扩展了傅立叶变换在工程和科学中的应用领域。

如果f是一个周期为1的周期函数，通过计算它的傅里叶系数就可以获得大量有关f的信息。这一点在理论上和实践上都是如此，而由于实践上的理由，非常希望有一种好的方法来快速地计算傅里叶系数。

第r个傅里叶系数是由以下公式给出的：

如果没有f的显式的公式来计算上面的积分（例如当f是由物理讯号给出，而不是由数学公式给出时，就是这样），就需要从数值上来逼近这个积分，而做这件事的自然的方法是把它离散化，就是把积分换成以下形式的和：

如果f不是震荡得太剧烈，r又不太大，这将是一个好的逼近。

如果对上式中的r加上N的整数倍，这个积分和的值不会改变，所以只需考虑f在形如n/N的点处的值。同样，因为f以1为周期，所以若对n加上N的整数倍也不会影响上式。既然对r和N都允许加上N的整数倍，所以可以认为r和N都是群Z_N（整数 mod N所成的群）。现在把记号稍作改动来反映这件事：给定了一个定义在Z_N上的函数g，定义同样是定义在Z_N上的函数

式（1）

为g的离散傅里叶变换（以下简记为DFT），其中用ω来代表

所以

注意这里的求和就是对n从0到N-1求和，和前面一样。再有一个记号变化就是用g(n)代替了f(n/N)。

DFT可以看成是用一个N×N矩阵

去乘一个列向量

所以这里需要N^2个算术运算。快速傅里叶变换（以下简记为FFT）的出现则是由于看到了(1)中的和具有的对称性质，使得其计算可以更加有效地进行。当N为2的幂时，这一点最容易看见，而为了做得更加容易一些，令N=8，想要求的和是

其中的r也取从0到7的某个整数值。这样一个和可以重写为

有趣的是

和

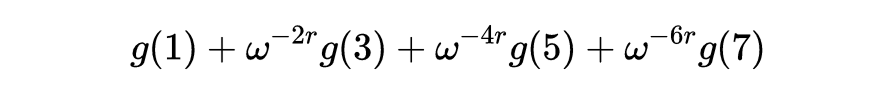
都是某个函数的DFT。例如，设

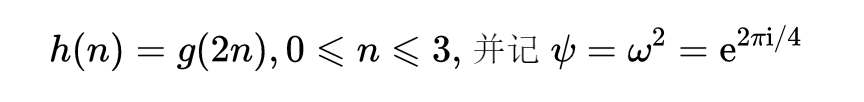
则上面第一个式子现在就成了

如果我们认为h是定义在Z_4上的，这恰好就是h(r)的公式。

对于第二个表达式，也可以作类似说明，所以，如果对g的“偶部”和“奇部”作DFT，就很容易直接得到g本身的傅里叶变换的每一个值，这个值只不过是偶部和奇部的傅里叶变换值的线性组合而已。这样，若N是偶数，用F(N)来表示计算定义在Z_N上的函数的DFT所需要的算术运算的次数，就会得到以下的递推公式：

这个公式的意思就是：如果要算出定义在Z_N上的某个函数的傅里叶变换的N个值，只需作两次定义在Z_(N/2)上的函数的傅里叶变换的N/2个值，再加上N个线性组合，每一个需要一个常数步数。

如果N是2的幂，就可以用迭代方法进行如下：F(N/2)是2F(N/4)+CN/2（但这里的C与上面的可以不同）。并仿此以往，不难证明，最后的结果是

其中C是某个常数，比之CN²这当然是很大的改进。如果N不是2的幂，上面的论证当然不行了。但是对这个方法可以作某些修正，并得到类似的效率的收益（事实上，对于任意有限阿贝尔群上的傅里叶变换，这都是对的）。

一旦我们会有效地计算傅里叶变换了，有许多其他计算也同样变得容易了。逆傅里叶变换是一个简单的例子，因为它有一个类似的公式使它也可以类似地来计算。再一个例子是两个序列的卷积，其定义如下：若a=(a0，a1，a2…，am)，b=(b0，b1，b2…，bn)是两个序列，它们的卷积就是序列c=(c0，c1，c2，…，c(m+n))，其中的cr定义为

序列c记作a*b。傅里叶变换的最重要的性质之一就是“变卷积为乘积”，就是说，如果有了一个适当的方法把a和b都看作Z_N上的函数，则a*b的傅里叶变换就是一个函数

所以想要做出a*b，只需作出

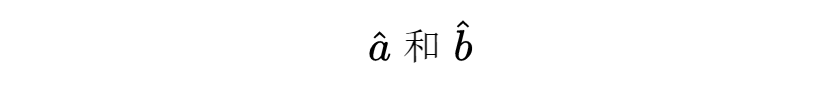
把它们乘起来，再作其积的逆傅里叶变换。计算的每一个阶段都很快，所以整个计算也很快。

这导出一种求两个多项式：

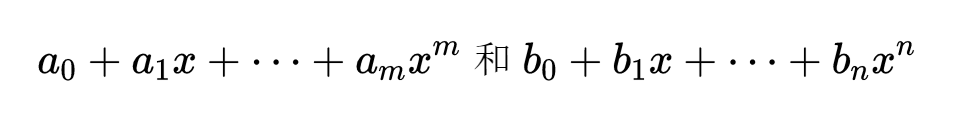
的乘积的快速的方法，因为它们的乘积的系数正是由系列c=a*b给出的。如果所有的a都在0到9之间，就有了一个计算两个多项式在x=10处之值的快速的方法（因为每一个系数cr的位数都不高），所以也就有了一个计算两个n位数的比长乘法更快的方法。这样，就有了快速傅里叶变换的为数巨大的应用中的两个。工程是一个更直接的应用的来源，因为在工程中，我们时常想通过研究信号的傅里叶变换来分析这些信号。它对于量子计算的应用是非常惊人的，Peter Shor有一个著名的结果，就是可以用量子计算机来非常快地对大数作因数分解，这个算法很本质地依赖于快速傅里叶变换，但是又奇迹般地应用量子计算机的能力，把Nlog N步分成N批，每批logN步，而这N批可以“并行计算”。