小王和小李既是同学,又是邻居。每个月,他们总是相约到一家小店买白糖。假设白糖的价格是变化的。
但是,他们的购买方式不一样。小王每次总是买一斤白糖,而小李每次只买一元钱的白糖,不管能买多少。
试问,这两种买糖的方式哪一种合算?
什么叫做“合算”?单看谁买的糖多是不对的,单看谁花的钱少也是不行的。应当计算各人平均每斤糖花了多少钱,谁少谁就合算。
假设他们在一段时间内买了n次糖,每斤糖的价格分别是a₁,a₂,...,aₙ(元)。
小王每次买一斤白糖,共花了a₁+a₂+...+aₙ(元),得到了n斤白糖,因此平均每斤白糖的价格为

图片
这个数称为a₁,a₂,...,aₙ的算术平均数。
小李每次只用一元钱买糖,所以一共花了n元。但他每次得到的白糖的斤数分别是

图片
因此平均每斤白糖的价格是

图片
这个数称为a₁,a₂,...,aₙ的调和平均数。
现在问题转化为:对于同一组正数a₁,a₂,...,aₙ,是算术平均数大还是调和平均数大?
答案是,当一切a₁,a₂,...,aₙ都相等时,这两个平均数是相等的;如果a₁,a₂,...,aₙ中至少有两个不相等,那么算术平均数大于调和平均数。也就是说

图片
不等式的等号当且仅当a₁=a₂=...=aₙ时成立。
所以,只要白糖的价格有波动,那么小李的购买方式比较合算。
这个道理容易理解,因为价格便宜时,小李买的多,价格贵时,小李买的少。
上面这个不等式的证明,请看下个单元。
从n=2做起上个单元中的最后一个不等式,可以变形为:若a₁,a₂,...,aₙ是正数,那么总成立着不等式

图片
不等式中的等号当且仅当a₁=a₂=...=aₙ时成立。
这是一个含有n个量a₁,a₂,...,aₙ的不等式,一个有效的方法是,先做n=2,再做n=3,从中看出某种规律,然后再来解决最一般的情况。
在生活中,我们也常常用到这种方法。比如,先吃肉,后啃骨头。
当n=2时,我们有两个正数a,b,需要证明的不等式是

图片
利用分配律将上式左边展开

图片
因此我们应当来证明
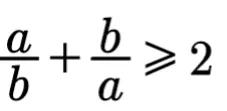
图片
上式相当于

图片
将上式左边通分,立即得出

图片
等号当且仅当a=b时成立。n=2的情况这就证明完了。
设n=3,这时考虑三个正数a,b,c。利用分配律

图片
前面我们已经指出

图片
(1)式等号当且仅当a=b时成立。
(2)式等号当且仅当a=c时成立。
(3)式等号当且仅当b=c时成立。
因此

图片
式中等号当且仅当a=b=c时成立。这样就证完了n=3时的情况。
现在,我们已经看清了对于一般的n,如何来证明这个不等式。
首先,反复利用分配律把表达式

图片
乘出来,得到一共有n²个项的多项式。这些项中,有n项
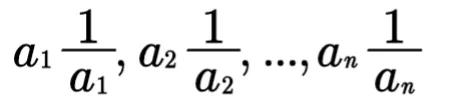
图片
等于1,其余的项一共有n²-n项,把这些项两个两个地配对,加上括号,配对的方式为

图片
等等。这样,一共可配为(n²-n)/2对。但因每对之和都不小于2,因此
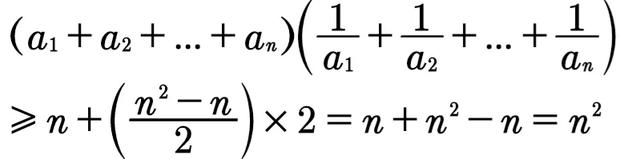
图片
这就得出了一般的结论。
尾声在证明上述不等式的时候,分配律起了很大的作用。在日常生活中,分配律有时会帮我们的大忙。
比如说,妈妈出门的时候,给你和妹妹留下了两张烙饼,它们都是圆形的,但是一张大一张小,一张厚一张薄。妈妈一再嘱咐你应当分得公平,谁也不能多吃多占。
怎么办呢?知道分配律就好办了。请看下图:

图片
这就是说,只要把每一张烙饼沿着一条直径切一刀,就很公平地一分为二了。
科学尚未普及,媒体还需努力。感谢阅读,再见。
