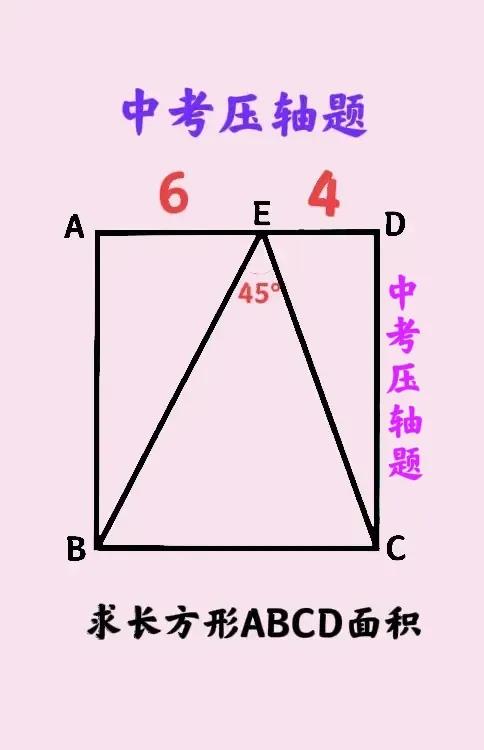
鱼和熊掌不可兼得，陷入“两难”：简单直观的方法，计算量大；计算量小的方法，难度大

鱼和熊掌不可兼得，陷入“两难”：简单直观的方法，计算量大；计算量小的方法，难度大、还不容易想到！这是某省中考数学压轴题：长方形仅一边已知，求其面积！ 如图，点E为长方形ABCD边AD上，AE=6，DE=4，∠BEC=45°，求长方形ABCD的面积。 考查知识点：①勾股定理②三角形相似！ ———————————— 提示一：最简单方法、但计算量大！ ①过点C作BE的垂线CF（也可过点B作CE的垂线）。 ②设AB=x，依据勾股定理求得BE²=36+x²，CE²=16+x²，CF²=1/2CE² ③依据面积性质S长ABCD=2S△ABC可得10x=BE×CF÷2也即800x²=BE²×CF²=(36+x²)×(16+x²)！ 提示二：计算量最小方法、但难度大！ ①将AD向左右分别延长至点M和N，使得AM=DN=AB，连接BM和CN，显然△ABM和CDN均为等腰直角三角形。 ②记∠ABE为α，则∠CED=135°-α，从而∠ECN=∠ECD+45°=90°-∠CED+45°=α=∠ABE，故△BEM∽△ECN（相似），进而EM/CN=BM/EN也即EM×EN=BM×CN。 ③设AB=x，则BM=CN=√2x，由②可得(6+x)(4+x)=2x²！ ————————————— 友友们，怎么看？欢迎留言分享！ #初中数学# #中考数学#