“全军覆没,难倒一众学霸、尖子生!”同学们纷纷表示,完全没头绪、根本无从下手!家长们认为题目超纲了!这是一道小学六年级数学竞赛题:仅已知正方形内一线段长,咋求其面积? 如图,正方形BCDE内1个四分之一圆及1个半圆,其交点为点A和点C,AB=4,求正方形的面积。 —————————— 提示:图形分割!有超纲嫌疑! ①记BC的中点为O(半圆圆心),连接AC和OD,其交点记为F,则BA垂直AC,OD垂直AC。 ②延长BA,与DE相交于点G,则G为DE的中点。 ③同于步骤①,连接点E与CD的中点,连接C和BE的中点,可将正方形分成4个与ABC相同的直角三角形,及中间一个小正方形。 ④小正方形边长AF=AB=4,AC=8。 友友们,怎么看?欢迎留言分享! #小学数学# #妙笔生花创作挑战#
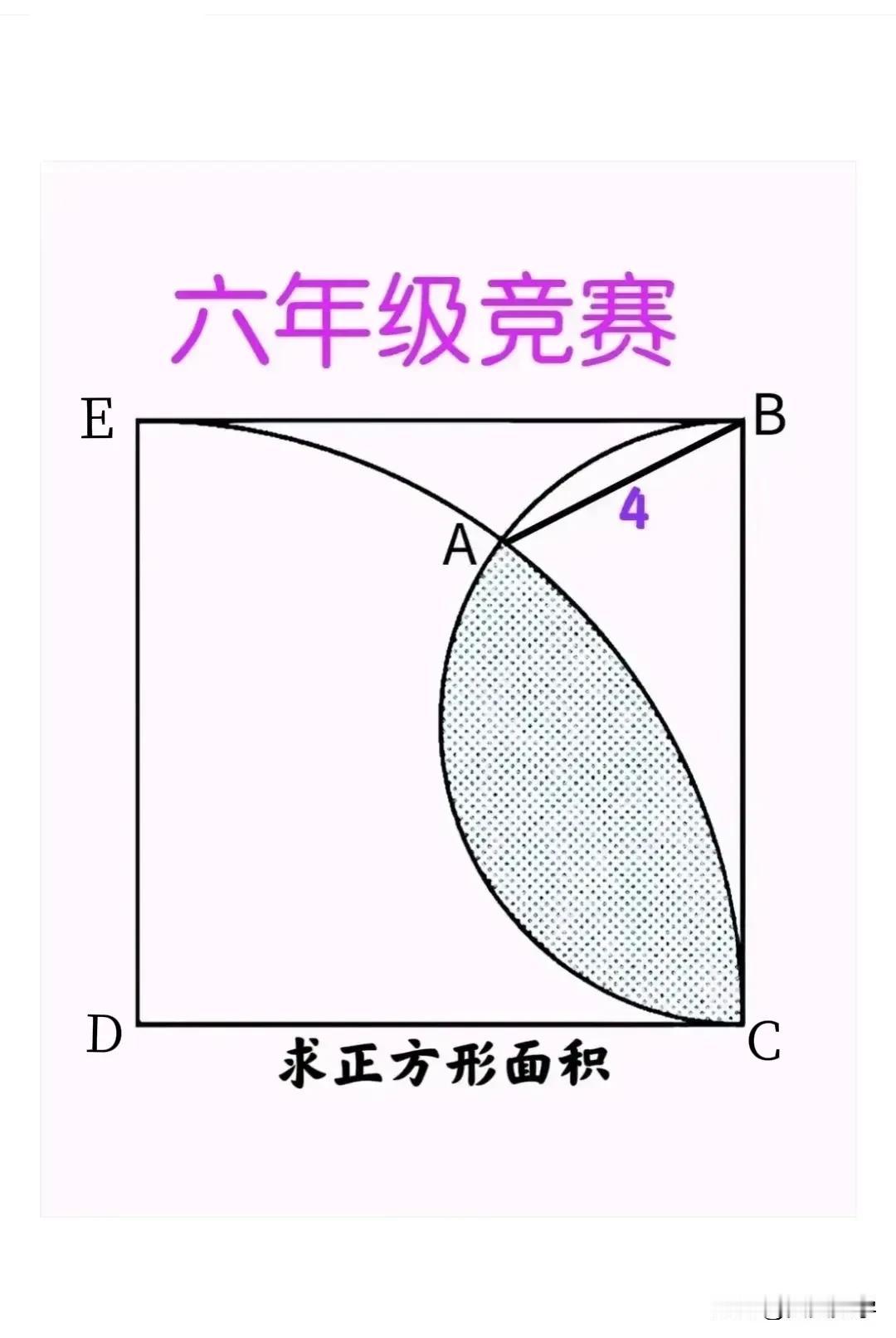
连接AC,过D点做AC的垂直线相交为F点,三角形ABC和三角形CFD为全等三角形,即CF=AB=4,三角形ACD是等腰三角形,则AF=CF=4,AC=8,正方形面积BC平方=AB平方+AC平方=16+64=80

韩雪松
①的两个结论分别由“直径对应圆周角为90°”和“圆心连线垂直于公共弦”得出,超纲严重。
亚楼
试用小学知识解此题,把另外三条直角边均做半圆,另三个角均做半圆,就可以得出FC=8,然后又勾股定理算出边长平方为80,从而正方形面积为80。
亚楼
用我上学时候初二的知识来解本题,过程如下:解:BC中点O就是小圆的圆心,连接BO,连接AC交BO于F,于是∠CFO为直角,∠ACB+∠FCD=90°,于是 ∠ACB=∠FDC,∠FDC=∠ABC,又∵DC=CB,因此△ABC≌△FCD,∴AB=FC=4,又∵AO垂直平分AC,即AF=FC=AB=4,∴AC=8,∴BC²=AF²+AB²=8²+4²=64+16=80。即正方形面积为80,解毕。
harry
80
东方红日
小学压轴题,基本都是超纲题
用户12xxx13
即使做出来了,以后考不上编制还是送外卖
UNI
32
亚楼
我读的初中二年级才接触几何,初二才学习勾股定律,现在知识都下放小学了吗?看来十二年初等教育学制真的太长了,看来应该九年初等教育制到时机了,刚好丢免费教育。