这是一道小学三年级附加题，不愧是奥数难度的题目，属实让同学们冒冷汗！ 要求在九宫格填数字满足所有的横行竖行斜行三个数字之和都相等。 这种类型的九宫格题目就是三阶幻方，若题目已知条件给出足够的数字可以用交叉数的方法，数字较少的时候用三阶幻方规律思考。
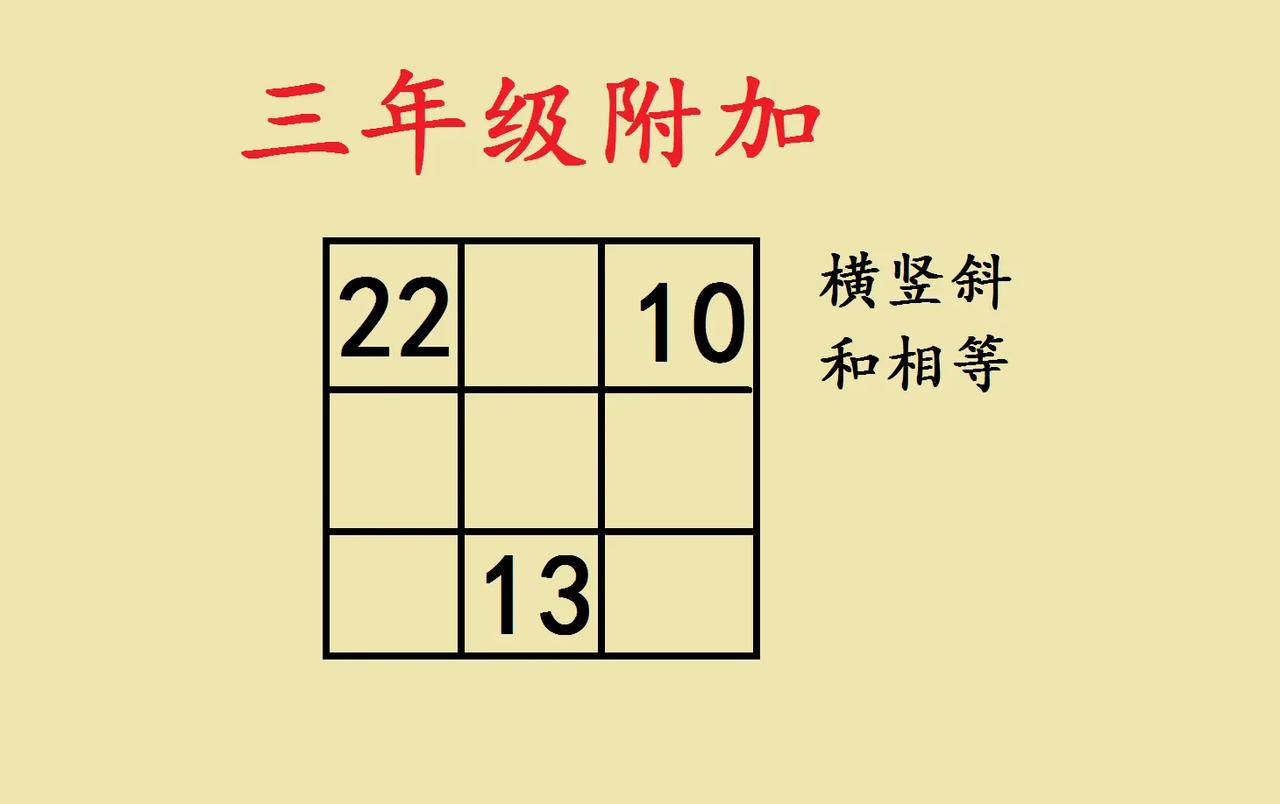
三数之和57，1—2：25，2—1：7，2—2：19，2—3：31，3—1：28，3—3：16。方法推理就行，22所在横排和13所在竖排有一个重合数，所以中间数字为22+10-13=19，接下来同理推理出两个斜行，可以得出三数之和，可以任意发挥了。
这是一道小学三年级附加题，不愧是奥数难度的题目，属实让同学们冒冷汗！ 要求在九
大力小学数学吖
2025-03-27 16:37:25
0
阅读：119
周明科
第一排25。第二排7---19--31第三排28--16。
眼睛的主人 回复 03-27 22:29
只有7、19、16三个数是确定的。。。
眼睛的主人
上中设1+x. 其余格子能用x表示. 但至少有一个不能..然后得出答案。。
岁月无声
22-13-10，13-19-13，10-13-22
三蜂
22+10=13+中，得中为19。余类推
二牛的老歌
抛开答案不谈，我小时候用16元一次方程来做四阶幻方，'将1-16填入16宫格中，打脸啪啪响。不知道三阶幻方能不能用九元一次方程解出来。已知条件是9个确定但没有定位置的数。
瑞佳橱柜
中间19，左下28，右下16，中左7，中右31，中上27，相加和57。
周明科 回复 03-27 22:10
中上25
周明科 回复 03-27 22:09
你错了.竖位第二排27+19+13不是57
眼睛的主人
所以右下角=-9?
周明科 回复 03-27 21:44
每三个加起来57。