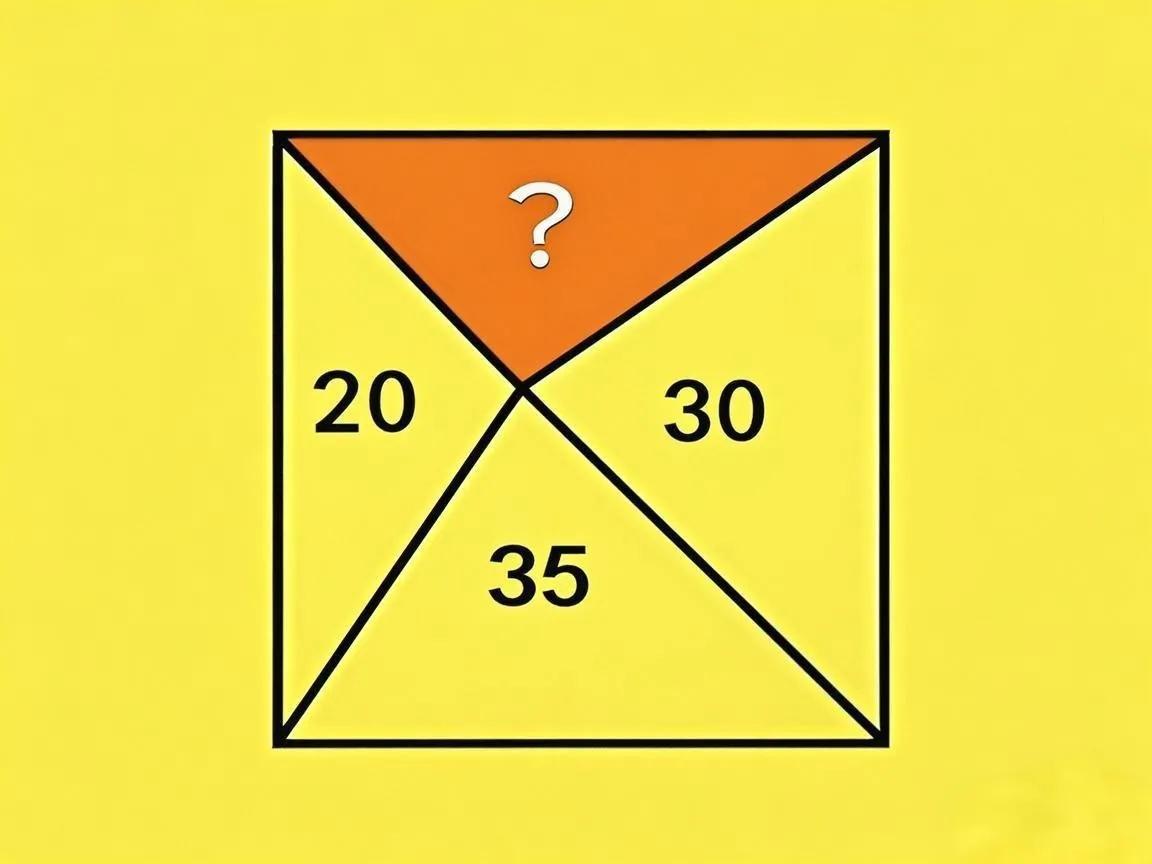
一道五年级的数学附加题，可把孩子们难坏了。题目是求图中阴影部分的面积。就这么一个看似简单的几何图形，却让不少小神兽抓耳挠腮。 这是一个正方形，被几条线分割成了几个三角形，已知其中三个三角形的面积分别是20、30和35 ，要求出阴影部分的面积。很多孩子看到这题，第一反应是懵圈。毕竟五年级学的几何知识有限，不像高年级有那么多定理和方法可用。 其实解题关键在于利用三角形面积的关系。我们知道，等底等高的三角形面积相等。在这个正方形里，我们可以通过对已知面积的三角形进行分析和组合。比如，观察这些三角形之间底和高的联系。经过一番思考和计算，我们会发现，阴影部分的面积可以通过一个巧妙的比例关系得出。 这道题看似难，实则是对三角形面积知识灵活运用的考查。孩子们要是能静下心，从面积公式的本质出发，去分析图形中底和高的关系，就能找到解题思路。大家不妨也让家里的小神兽试试这道题，看看他们能不能挑战成功呢？
（20+30）×2=100，边长为10，面积为100，100-30-20-35=15。交点o画一条线为20和30的高分别为a,b。a+b＝边长x。xa/2+xb/2=20+30=50=xx/2,面积xx=100
设正方形边长为a，过交点分别向四边做垂线，h1、h2，h3、h4，则，h1+h2=h3+h4=a，左右两个三角形面积和=1/2（a*h1）+1/2（a*h2）=1/2（a*（h1+h2））=1/2（a*a），上下两个三角形面积和=1/2（a*h3）+1/2（a*h4）=1/2（a*（h3+h4））=1/2（a*a）。所以，左右两个三角面积=上下两个三角形面积，因此阴影面积=20+30-35。
可先算出正方形边长为10.所以正方形面积为100.阴影面积S=100-20-30-35=15
一点零七
15
总有刁民想害朕
一半模型口算都能出结果，阴影面积25
周明科 回复 05-22 13:31
真笨，同底等高30+20-35
才华大道 回复 06-13 17:30
思路清晰，就是结果不对！
用户16xxx88
以正方形对角线平分正方形来看，S阴+30=20+35，S阴=25；从面积公式的本质出发，等底等高的三角形面积相等来解，S阴+35=20+30，S阴=15。。。请问：这图，你想怎么解？
用户95xxx57 回复 05-20 23:14
30≠35，因此绝对不存在对角线平分
用户32xxx27 回复 04-22 19:07
不存在对角线，假设不成立
砖头打歪了
35+？=20+30，所以是15
用户10xxx38
四元一次方程组
暖意序言
瞪眼法面积20，30的两个三角形面积和等于正方形面积的一半，所以20+30-35=15
用户64xxx50
20/X=35/30 面积X=17.14285714
用户10xxx38 回复 06-22 14:30
四个三角形都不相似，虽然底也相等，但高不成比例，所以面积也不成比例，这个答案是错的，正确答案是15.
用户15xxx35
S20和S30两个三角形同底共高，所以20+30=1/2S□，由逐个减去可得15
用户2025
20+30-35=15
用户10xxx48 回复 04-21 12:02
正雀！
用户11xxx72
20+35-30=25
漫游者
算出25的都少了个0
左右
这个题不配成为附加题，考点单一。
四代老海
25
成为有关
先说说20是什么吧 从头到尾让别人猜 不如猜灯谜还有奖